Концептуальный вопрос. Можно ли произведение считать частным случаем свертки?
Посоветуйте, пожалуйста, книгу по теории типов для TCS.
Нет, с чего бы?
Как называется точка О?
>точка О
Где ссылки на архивач?
Я хочу видеть как игра из гуглпеля про основы гееметрии времен пифагора унижает местных топологов уровня буэ.
http://pdalife.ru/pythagorea-android-a22036.html
инб4 ГЕЕМЕТРИЯ НИНУЖНА, НИМОТИМАТИКА
http://pdalife.ru/pythagorea-android-a22036.html
инб4 ГЕЕМЕТРИЯ НИНУЖНА, НИМОТИМАТИКА
Ну умножение матриц - свертка по определению. А свертка многочленов относительно умножения и композиции вырождается в простое умножение по школьным правилам. Вот я и подумал.
хочу вкатиться в статистику
подкиньте книжек
читай любую хуету из гугла, всё равно у тебя нет таланта, а для прикладых задач и википедия сгодится.
херню сказал и книжек не посоветовал
бывает:(
Где бугурты от невозможности проведения срединной линии к отрезку?
Как составить линейное уравнение прямой Ax+By+Cz+d по направляющему вектору(т.е. известны две точки)?
>Ax+By+Cz+d
Это уравнение плоскости
Блджад, я совсем видимо поехал...
По двум неколлинеарным векторам - берёшь векторное произведение - это нормаль, т.е. (A,B,C). Для того, чтобы определить D теперь нужна точка на плоскости.
Посочетуйте что то про векторный анализ, чтобы там как для двачера все было описано и разъяснено.
Так, мне через 9 дней сдавать вступительные в МухГУ, прошел 69 страниц Шеня, времени нет, подскажите, какие темы основные изучить, чтоб сдать. Наверняка что-то можно пропустить.
Сосание хуя у приемной комиссия для чайников
А че, в 2016 бывает такое, что принмают не по ЕГЭ?
Да, если после колледжа.
То есть, ты учился 9 классов в школе, а потом еще 3 года в ПТУ колледже и твои знания по математике умещаются в 69 страниц учебника для самых маленьких детей?
Ну, я не совсем учился, скорее проебывал все пары и скроллил /b/.
Кроме того, ты реально тупой. Когда проводится экзамен, заранее известен список тем, которые надо подготовить. Вместо того, чтобы найти этот список или позвонить в универ и спросить, ты спрашиваешь на дваче, какие темы тебе надо готовить к экзамену.
Собирался поискать, но забыл. Спасибо.
Блядь, можете мне сказать блядский ответ и пояснить, почему так?
>in any commutative ring
No. 2x=1, y=1, в Z.
>in any field
Yaass. Гаусс.
Разве системе уравнений первого порядка не всегда должна удовлетворять ровно одна пара чисел x и y? На то ведь она и система.
Ровно - не всегда.
x + y = 1
2x + 2y= 2
>No. 2x=1, y=1, в Z.
Fuk! Can u tell me a meaning of this line? What do u want me to say through this?
Sorry, I'm so fkd stupid! kkkkk? А про поля я и так знал, блядь!
Хуйня эти ваши множества
Решений в Z нет, 2x=1 же, хотя система подходит под условие.
Не, ну я имею в виду нормальные системы, а не те, когда переменные самоустраняются.
Так в этой теореме и говорится этот факт.
Я так про категории думаю.
ssssen.q!
Нам нужна замена математики
Предлагаю огурец.
Блин, нашел бы более смешное и несуразное слово. Типа кронштейн или коржик.
2D - радиан
3D - стерадиан
4D - ?
Есть какое-нибудь название?
3D - стерадиан
4D - ?
Есть какое-нибудь название?
> Первая точка Торричелли — точка треугольника, из которой все стороны видны под углом в 120°. Она существует только в треугольниках с углами меньшими 120°, при этом, она единственна и, значит, совпадает с точкой Ферма.
Бамп вопросу, ну.
Какая разница, эти названия всё равно никто не использует.
>точка Торричелли
В этот тред стоит заходить хотя бы для того, чтобы каждый день узнавать какой-нибудь новый термин.
Вот вы говорите, что интегралы не нужны, а что-то вольфрам альфа не может посчитать интеграл, который довольно просто берется.
Хочу доказать, что ряд 1/(n (ln n)^p) сходится при p > 1 и расходится при p <= 1. Интеграл от 1/(x (ln x)^p) на [2; Inf] вольфрам альфа не может посчитать
http://www.wolframalpha.com/input/?i=integral+1%2F(x+(log+x)%5Ep),+x+%3D+2+to+a
Частный случай p = 1 тоже не может посчитать
http://www.wolframalpha.com/input/?i=integral+1%2F(x+(log+x)),+x+%3D+2+to+a
А между тем интеграл довольно простой: надо сделать замену ln x = t.
Может, я как-то не так вольфрамом альфа пользуюсь? Или, может, в оффлайн версии все работает? Но я студент, у меня нет 300 баксов на вольфрам математику.
Хочу доказать, что ряд 1/(n (ln n)^p) сходится при p > 1 и расходится при p <= 1. Интеграл от 1/(x (ln x)^p) на [2; Inf] вольфрам альфа не может посчитать
http://www.wolframalpha.com/input/?i=integral+1%2F(x+(log+x)%5Ep),+x+%3D+2+to+a
Частный случай p = 1 тоже не может посчитать
http://www.wolframalpha.com/input/?i=integral+1%2F(x+(log+x)),+x+%3D+2+to+a
А между тем интеграл довольно простой: надо сделать замену ln x = t.
Может, я как-то не так вольфрамом альфа пользуюсь? Или, может, в оффлайн версии все работает? Но я студент, у меня нет 300 баксов на вольфрам математику.
>Интеграл от 1/(x (ln x)^p) на [2; Inf] вольфрам альфа не может посчитать
Может http://www.wolframalpha.com/input/?i=integral+1%2F(x+(log+x)%5Ep),+x+%3D+2+to+infinity
Что делать, если есть мат. книга, которую тебя позарез нужно через "нимагу" осилить, но она не твоего уровня, половина базовых не объясняющихся автором определений тебе непонятна?
Где и как искать информацию? Позарез.
Где и как искать информацию? Позарез.
Я думаю об углах многомерных многогранников, дефектах при вершине и т. п. Хочется как-то называть - думал, может, есть слово.
1. Литература в конце книги
2. enwiki.
Поподробнее нельзя ли?
Не говори загадками. Всё зависит от обстоятельств.
> никто не использует
Как минимум используют те, кто занимается геометрией. настоящей, в смысле, а не дрочевом про последовательности пучков
Там даже никакой библиографии в конце книги, блядь!
Вот эта книжонка - rgho .st/69fwR6y97 - мне нужно выучить её материал, но я нихуя не понимаю. Да, это gradaute-level, но что я могу.
Что делать?
а вот за пучки ты ответишь своим ебалом.
Пиздец какой-то. Такими книгами только ньюфагов пугать наряду с программой Вербита.
> Там даже никакой библиографии в конце книги, блядь!
Я вот полистал и на страницах 50 и 98 нашел references.
Блядь! То есть, я пропал?
>Mexico, 1987
Охуеть
Что?
Где ты вообще откопал этот конспект? Ты учишься в мексиканском вузе? Почитал бы для начала хоть Шафаревича "Основы алгебраической геометрии".
Можете хотя бы в двух словах пояснить, что на скринах за хуйня творится? После этого сам разберусь. Я так понимаю, это основополагающая теорема всего section.
Есть тут хотя бы один graduate-знаток?
Или стоит зашквариться и идти на dxdy?
Есть тут хотя бы один graduate-знаток?
Или стоит зашквариться и идти на dxdy?
>Где ты вообще откопал этот конспект?
Не могу сказать. Но это не я откопал.
Основы то я, блядь, знаю. Но не помогает.
Посоны, серьезный вопрос. С какого хуя у квадрата/круга сумма углов 360 градусов? Почему не 100, почему не 200?
Почему?
Если бы, например, принять что сумма углов круга, например, 140 градусов, то тогда бы можно было спокойно разделить круг на 7 равных секторов.
Почему?
Если бы, например, принять что сумма углов круга, например, 140 градусов, то тогда бы можно было спокойно разделить круг на 7 равных секторов.
У древних шумеров была двенадцатеричная система исчисления. Количество градусов к круге и секунд в минуте (минут в часе) - наследие древних.
Считать величину угла равностороннего треугольника равной именно 60 неким единицам - это традиция, идущая из древнего Междуречья, где была шестидесятеричная система счисления. Оттуда же идёт традиция делить час на 60 минут, минуту - на 60 секунд.
Если не нравятся градусы - есть, например, грады. Один град - 1/100 часть прямого угла. Есть радианы. Можно и какие-нибудь более экзотические единицы измерения плоских углов ввести, если тебе с ними будет удобнее.
> С какого хуя у квадрата/круга сумма углов 360 градусов?
Чаво?
Где у круга углы и как посчитать их сумму?
> тогда бы можно было спокойно разделить круг на 7 равных секторов
Чаво?
А сейчас спокойно разделить круг на 7 равных секторов нельзя? Только с волнением и дрожью сердца?
Во ещё, например.
https://ru.wikipedia.org/wiki/Румб
Блин, аж захотелось опубликовать какую-нибудь статью по геометрии, где все углы будут в румбах.
Думающий о многогранниках
https://ru.wikipedia.org/wiki/Румб
Блин, аж захотелось опубликовать какую-нибудь статью по геометрии, где все углы будут в румбах.
Думающий о многогранниках
Что значит "позарез выучить"? Это же даже не какой-то учебник, а сборник конференции.
Я не могу сказать, говорил же уже.
Мне нужен этот материал. Это конференции, редактированные под учебные лекции.
> Я не могу сказать
Что-то это всё подозрительно..
Ты в плену в мексиканском наркокартеле?
Математики никогда не используют градусы, все используют радианы, так что это не математический вопрос.
Толсто.
Бамп еще раз
60-тиричная. Двенадцать фаланг пальцев на одной руке, большой палец в качестве счета был, и пальцы нга другой руке для обозначения целого количества полностью посчитанных фаланг
Это только одна из версий, есть и другие.
Почему у них была именно шестидесятеричная - точно неизвестно.
rgho .st/7MTLqWmHd
Базарю, эта правильная. Читал у какого то васи-археолога статейку.
Вишнею с майнером не забыл положить?
А на русском что то есть? А то НИПАНЯТНА НИХУЯ!!!
>Математики никогда не используют градусы, все используют радианы
Я картошку сварил, а ты что за бормотуху взял? Сколько радиан там хотя бы?
Математики никогда не употребляют алкоголь. Они употребляют теорию групп. Так что это не математическая ситуация.
Я правильно понимаю, что ни одно из отображений пикрелейтед не является сжимающим? (сжимающие отображения в этой книге называют сжатыми) Просто я удивился, что вопрос так формулируется и при этом ни одного сжимающего отображения. Подумал, что может я что-то не так понял.
Как построить группу Ли без СМС и регистрации?
У шумеров были и 60-ричная и 12-ричная. 60-ричная использовалась для математики, 12-ричная для повседневных нужд и астрономии. В сутках 24 часа именно потому, что шумеры использовали 12-ричную систему, которую у них переняли египтяне.
Лошь
Лол, не хочешь - не верь. Но я, на твоем месте, сначала википедию хотя бы почитал, прежде чем такими словами раскидываться, диванный культуролог.
А в часе 60 минут, в минуте 60 секунд, из за того они сильно в математиков заигрались, да!?
В древнем мире не было понятия минут и секунд. Сутки делили на 24 часа (причем не равной длины), подтверждений деления часов на более мелкие промежутки, в доантичный период, пока не найдено. Понятие минут и секунд, да часов в современном понимании, пришло чуть ли не с системой СИ.
Как же периоды "пока летит стрела" или "столько-то ударов сердца"? Не, ты пиздишь.
Не, не пизжу)))))))0 Это как сейчас сказать "в двух шагах" или "за краткий миг" - бытовая фигура речи, не имеющая четкого эквивалента. )))
Напомнили, племя такое есть в бразилских лесах, пиранья называется. У них в языке нет цифр. Есть только два понятия - чуть-чуть и дохуя. Какой-то белый хуй с ними много лет работает. Пытается их счету обучить. Говорит в целом необучаемые. Кроме может пары-тройки детей.
А, вот же ну тубе https://www.youtube.com/watch?v=nDM8G5tuHF8
А, вот же ну тубе https://www.youtube.com/watch?v=nDM8G5tuHF8
>зашквариться и идти на dxdy
ну давай, назад только не приходи опущенцем
давеча бакарди пил, у него на горлышке flame arrester. вот такой. это градусы или радианы?
Зачем им цифры? На языке переменных пусть изъясняются. Там уже и до гомологий недалеко.
третий норм, однобитный. битард?
как на дваче, да. они бы вписались.
Он просто мыслит отрезок связным множеством вещественных чисел и не может указать естественное его разбиение. В корень зрит.
Важный мат. вопрос: как дела у Ромы Михайлова?
у него сегодня достаточно простая лекция
Я увы не из дс2, поэтому лекция - это мимо меня, просто интересно, чем он занимается. ЖЖ-то он удалил свой.
У меня сомнения, как они вообще объяснили задачу. Вот выйдешь например на улицу и попросишь прохожих пальцем ткнуть - мне кажется большинство не поймет, что от них хотят. Ряд какой-то, отъебись от меня.
Так и всякие метры и секунды аж до 19 века не имели чёткого эквивалента, пока хитрые французы не замутили палату мер и весов. Которую к тому же постоянно обновляют.
Конечно простая, о гомологиях груп думать пятнадцать лет.
ШОК!!!!! НЬЮТОН ОТКРЫЛ СИЛУ И УСКОРЕНИЕ БЕЗ МЕРЫ ВРЕМЕНИ!!!! читать далее...
Берёшь прямую такую со сложением. И получаешь группу Ли.
Как бы нам побольше людей в наш тред заслать? Он интересный, но медленный.
Помните, как зимой в бамплимит уходили за два дня? То-то и оно.
Помните, как зимой в бамплимит уходили за два дня? То-то и оно.
может есть какой-нибудь задачник по школьной математике, чтобы в нём было не более 100 хорошо подобранных задач для повторения? задания нужны как егэшные так и более сложные.
Перестать задвигать про РАССОВО ЧИСТУЮ АРИЙСКУЮ ТОПОЛОГИЧЕСКУЮ МАТЕМАТИКУ, например тащемта однако
Ты что, мудак? Создай свой тред второй культуры и сиди в нём со своими дружками, быдло. А этот не засоряй. Прямо сейчас иди отсюда. Дальше не читай моё сообщение, животное.
Тебя нужно в клетку посадить и показывать. Натуральный мент.
Я говорю о том, чтобы набрать людей нашей аудитории.
не бомби, картофан
Картофан это тут только ты.
зимой цыган был еще.
Кто это?
Какую книгу читать если хочешь все вспомнить/повторить чему учили в школе с 7 класса?
Кино лучше.
Ожидаемый ответ.
Надеюсь все таки один нормальный анон посоветует годноту.
Брошюры МЦНМО
Очевидно, Бубрбаки.
бурбаки функция действительной переменной и непрерывные группы, или как-то так
Стоит лт решать все задачи? А то я не могу решит все задачи в конце параграфа в Зориче.
>ли
-самофикс
не стоит. Будешь топтаться на одном месте. Решай что сможешь и двигайся дальше.
В природе существуют задачники по анализу/алгебре где есть ответы к задачам на доказательство?
Если ты можешь представить, где можно использовать утверждение, которое тебе предлагают доказать, то стоит поупираться подольше. Если не сможешь доказать, нагугли решение или спроси у кого-то.
А если ты не представляешь, как задача могла возникнуть и зачем ее надо решать, то не стоит даже начинать ее решать: если у тебя не будет осознанания того, зачем это нужно, через месяц ты уже ее забудешь и можно будет считать, что ты ничего не решал. А время будет проебано.
Конечно. Гуглишь "<book-name> solution manual". Вот solution manual к Рудину например:
https://minds.wisconsin.edu/handle/1793/6700
К учебнику по алгебре Axler: Linear Algebra Done Right тоже есть солюшн мануал.
Может конфу создадим для математических нубов? Типа раковой техноконфы, но посерьезнее?
давай пили. типа вопросы тупые и еще тупее. у меня первый тупой вопрос - как определить N
Кто в телеге есть - го тупить вместе
https://telegram.me/joinchat/DLtW7z-4NKM3eLPVZot7Kg
https://telegram.me/joinchat/DLtW7z-4NKM3eLPVZot7Kg
Помогите кто-нить с этой хуйней, в чем ошибка?
Вот с этой еба
Теорема фаллоса. Гы-гы.
Нахуя это делать? Религия запрещает здесь писать? Анонимность раздражает? Ракошкольники.
Хуй знает в чем ошибка, мне лень читать твои школьные каракули, но там теорема Фаллеса не нужна никакая, задача решается устно. Просто постарайся приравнять оба указанных угла к любому из двух равных у основания равнобедренного треугольника.
Thank you
Моча забоялась.
А вообще, нам нужна отдельная мини-борда.
Nenujna.
Математиков в сци больше остальных постоянных посетителей, но их абсолютная величина слишком мала для отдельной доски.
Так их больше появится. Математическим обсуждениям слишком не подходит то быдло, что периодически заходит сюда с /b.
Откуда их больше появится? ДХДУ сюда переедет? Сомневаюсь. А быдло будет заходить и на отдельную доску. Не надо плодить сущности.
>подходит то быдло, что периодически заходит сюда с /b
где оно здесь, примеры?
Ты, например.
Например я.
Тут никто мне так и не дал книжку понятную по векторному анализу.
Существует не только и не столько dxdy (да и там старьё, никогда не пойдут они на борды, они менты и рабы по жизни).
Но существует, во-первых, наплыв в наш тред неграмотных гуманитариев, во-вторых, наплыв в тред даже не гуманитариев, а просто спам-лиц, в-третьих, просто анальная модерация, которая удаляет всё и вся, чтобы создавать перед своими хозяевами из конфы видимость собственной "работы", в-четвёртых, Двач просто не адаптирован под мат. аудиторию - не то что формул в посте не набрать и графиков не построить, так даже простой знак умножения Makaba часто теряет, в-пятых, математика - это просто слишком широкая тема: мешает ли её обсуждению реклама какого-то говна снизу, сверху? Да. Это нематематический контент, нематематическая борда.
Вот и думайте сами, нужна нам мелко-борда или нет (хотите ли вы продолжать здесь жрать говно или нет)?
Мочух это может стереть, так что вот этот пост: pastebin .com/YhpAWNwc
Сейчас я дам. Тебе для физики или для pure математики?
Не дури. Все, кто хотел уже вкатились. Модератор иногда и правда делает странные вещи, но не критично. Отдельная мертворожденная борда никому, кроме тебя не нужна. 6
Говно-модератор делает говно, потому что "Неактивные модераторы будут удаляться" - старается перед хозяевами. Всеми силами мент старается!
Его и всю эту шайку нужно в клетку посадить и показывать - падающего подтолкни.
>Не дури.
Хочешь жрать говно, всё-таки.
Я хочу чтобы ты кукарекать перестал.
Как говно, вкусно, да? Ну так на, получай ещё! Жри, блядина!
Съеби уже, галоперидольный.
>галоперидольный
Смотрите! Смотрите! Я учу вас о сверхчеловеке! Тупая блядина даже не обладает базовыми грамматическими навыками.
Не повезло же быть тобой. Земля полна ненужных людей.
типичный ответ быдла. огульно охаивать. у меня публикации и хирш огого.
>хирш
Алекс Хирш?
Посоны, че у вас в матеше, эпоха накопления ошибок?
Для физики.
Похоже у N ципленка летнее обострение и он хочет зохавать всю математику вообще.
rgho .st/8Nf75HJsP
Быдло подъехало! Я взял вас за гнилое вымя и буду со всей злостью и силой выкручивать его, пока прилежащие артерии вашего витального тела с глухим треском не разорвутся, и вы не подохнете от кровоизлияния в ваши мерзкие зловонные внутренности. Говно, ты будешь просить и умолять меня пощадить бедное животное - тебя самого - но Я могу только хотеть смерти. А значит, Я не остановлюсь. А значит, ты умрёшь, ненужное создание. Никого рядом. Ты и Я.
И будут мои желания исполнены.
И так говорю Я. И да будет Так.
Каникулы же. К ЕГЭ готовится.
И?
Да, математика пиздец какая нестрогая. Сейчас самая важная задача - это полная формализация математики с помощью пруф асистантов. Я вот хочу немного осилить теорию гомотопий и потом HoTT читать.
>Сейчас самая важная задача - это полная формализация математики с помощью пруф асистантов
Proigral.
Посоветуйте, пожалуйста, лучшие книги по теории вероятностей и математической статистике, на английском языке. Или эти дисциплины за математику не считаются?
Чому? Ты не веришь, что с помощью пруф асистантов можно формализовать что-то кроме самых прмитивных вещей?
Я не верю, в то, что:
а) это самая важная задача
б) на пруф ассистанты непохуй вообще хоть кому-нибудь из работающих математиков, кроме разработчиков пруф ассистантов (вырожденные случаи типа классификации простых групп и теоремы о 4 красках не берём)
в) пруф ассистанты основанные на гипотетично-дедуктивной модели принесут хоть какой-то профит (в широком смысле) в ближайшем будущем
А какая самая важная задача? Какая-нибудь хуйня из алгебраической геометрии, которую понимает 10 человек во всем мире и которую ни в одной прикладной науке в ближайшие годы не применить?
> вырожденные случаи типа классификации простых групп и теоремы о 4 красках не берём
Я считаю, что в будущем такого будет больше. Будет нормой не знать всех доказательств даже в своей области, не говоря уже о смежных областях. Сейчас приходится дрочить на доказательства, потому что если их не знать, ты будешь хуже понимать, как все работает, и будет очень легко ошибиться. Если будут активно использоваться пруф асистанты, то они тебе просто не дадут ошибиться и ты сможешь в своей работе использовать очень глубокие и продвинутые результаты из областей, о которых ты имеешь только поверхностное представление, и не бояться ошибиться. В этом и профит.
>А какая самая важная задача?
Самой важной задачи нету. Важность - это оценочная категория определяемая в какой-то конкретной языковой игре какой-то конкретной тусовки. Если ты попадешь к науч.руку, который занимается Х, он будет считать, что Х - это очень важно. Мне казалось, это очевидно.
>Какая-нибудь хуйня из алгебраической геометрии, которую понимает 10 человек во всем мире и которую ни в одной прикладной науке в ближайшие годы не применить?
Ну, в алгебраическую геометрию сейчас вливается пиздец как много денег из-за теории кодирования. А про прикладную науку - лольнул, пруф ассистанты в какой прикладной науке применить можно?
>удет нормой не знать всех доказательств даже в своей области, не говоря уже о смежных областях. Сейчас приходится дрочить на доказательства, потому что если их не знать, ты будешь хуже понимать, как все работает, и будет очень легко ошибиться.
> и ты сможешь в своей работе использовать очень глубокие и продвинутые результаты из областей, о которых ты имеешь только поверхностное представление, и не бояться ошибиться.
LOL. Ты на первом крусе, наверное? Ты не поверишь, но работающие математики не знают 95% доказательств тех фактов, что они используют в своих статьях.
>Я считаю, что в будущем такого будет больше.
Каковы предпосылки?
Вообще мыслить математику как формальное дерево из формализуемых определений и теорем - это такой наивняк, что пиздец.
> пруф ассистанты в какой прикладной науке применить можно?
Насколько я знаю, их пока что используют при проектировании всяких микросхем. Типа если неправильно спроектировать, куча железа проебется. Я в этом не шарю, возможно, там не Coq, а какие-то другие пруф асистанты, основанные на других принципах, но я знаю, что пруф асистанты там реально используются.
> Вообще мыслить математику как формальное дерево из формализуемых определений и теорем - это такой наивняк, что пиздец.
Естественно, это не так и еще много лет будет не так. Но вот такая у меня мечта, потому что мне нравится ощущения уверенности, нравится чувствовать, что я все контролирую.
> Ты не поверишь, но работающие математики не знают 95% доказательств тех фактов, что они используют в своих статьях.
Кстати, как тогда изучать математику? Вот я читаю книгу. Что ты мне предлагаешь делать? Решать задачи в конце параграфа что ли? Но это же хуйня, там редко что-то интересное. Обычно я сам себе придумываю задачи. Стандартная ситуация: я что-то предположил, сформулировал утверждение, написал доказательство на бумажке. Ни в одном учебнике это утверждение не написано (не то чтобы я какой-то прорыв совершил, а просто утверждение маловажное, или, может быть, я просто найти не могу), поэтому нет никаких критериев проверки, кроме как внимательно просмотреть на записанное доказательство. А если я не вдрачиваюсь в определения и доказательства до каждого символа, как я смогу проверять свои доказательства?
Мне кажется гораздо полезнее воспринимать математику как набор философских учений, а не как плохо заформализованные тексты в какой-то дедуктивной системе. В математике очень часто определения "осовремениваются" чтобы лучше подбить их под интуицию современного сообщества, если же будет огромная БД из доказательств и определений, то кардинально изменить какие-то "низкоуровневые определения" уже никто рисковать не будет, ибо всё рухнет, что противоречит духу математики в целом.
>Ни в одном учебнике это утверждение не написано (не то чтобы я какой-то прорыв совершил, а просто утверждение маловажное, или, может быть, я просто найти не могу), поэтому нет никаких критериев проверки, кроме как внимательно просмотреть на записанное доказательство. А если я не вдрачиваюсь в определения и доказательства до каждого символа, как я смогу проверять свои доказательства?
А никак. У Коши в учебнике анализа вообще каждое второе утверждение было неправильно. Например, он "доказал" что любая непрерывная функция дифференцируема почти всюду и исторический опыт лично меня убеждает, что из современных утверждений неправильных где-то 50-70%, и лично я вижу, как проверяют мои доказательство мой научный руководитель и редакция научных журналов - очень поверхностно, поэтому я пытаюсь интуитивно охватить большинство фактов, а когда нахожу в интуиции ошибки - отношусь к этому вполне спокойно и корректирую их.
Иногда вдрачиваться до каждого символа целесообразно (когда статью пишешь или когда чувствуешь, что чего-то действительно плохо понимаешь), но в большнистве случаев - нет, достаточно просто уловить идею.
Ну это моё мнение, многие математики с ним не согласны.
> Мне кажется гораздо полезнее воспринимать математику как набор философских учений, а не как плохо заформализованные тексты в какой-то дедуктивной системе.
Ну я воспринимаю это и так и так. Т. е. интуиция и строгость идут бок о бок и поддерживают друг друга.
> из современных утверждений неправильных где-то 50-70%
Алсо, это же совсем пиздец.
Почему? Важны интенции и ощущения, а не истинность тех или иных утверждений.
> Иногда вдрачиваться до каждого символа целесообразно (когда статью пишешь или когда чувствуешь, что чего-то действительно плохо понимаешь)
Кстати, я так себе и представляю работу с пруф асистантами. Тот, кто пишет статью, будет к ней писать и код. Остальные этот код смотреть не будут - они могут его запустить у себя на компе, чтобы проверить, а читать они будут обычные человеческие слова, такие же как сейчас пишут в книгах. Ну или можно посмотреть этот код, если чувствуешь, что в чем-то плаваешь. То есть смысл в том, чтобы в конечном итоге люди меньше надрачивали доказательства и больше развивали интуицию.
А зачем тогда математика нужна вообще?
>математика нужна
Тебе - нет.
Ну, в современных парадигмах пруф ассистеров это выглядит малореально. Если в будущем придумают какие-то очень крутые интерфейсные решения, когда математику, чтобы формализовать своё доказательство не придётся тратить в двадцать раз больше времени, чем на его придумывание - то вполне возможно что так и будет. Но это утопия, особенно это плохо вкатывает в геометричных разделах, где остались proof by pictures даже в научных журналах (в векторных расслоениях и маломерной топологии, например).
Вопрос "Зачем нужно Х" можно задавать только предварительно специфицировав контекст и зафиксировав языковую игру, иначе вопрос не имеет смысла. Можно, например, спросить "Зачем нужна математика инженерам для их работы", но сам по себе вопрос "зачем нужно Х" несёт в себе не больше смысловой нагрузки, чем вопрос: "В чём смысл жизни?" или "Что такое Бог?". Думал на двачах-то такие простые вещи понимают.
>"В чём смысл жизни?"
42.
>"Что такое Бог?"
Я.
Еще вопросы?
Своей попыткой пошутить, ты неявно зафиксировал некоторую языковую игру. Другой может попытаться ответить на эти вопросы серьезно и зафиксированеть другую игру и получить, соответственно, другие ответы в её рамках.
Кстати, забавно, что в треде для новичков обсуждают целесообразность пруф-ассистантов и думают о всяком таком высоком, а в "серьезном треде" спрашивают что-то про определение интеграла. Ну вот и нахуя это деление было? Чтобы две вкладки в браузере занимать?
Чтобы у мочи больше работы было.
>пошутить
Wrong.
> Вопрос "Зачем нужно Х" можно задавать только предварительно специфицировав контекст и зафиксировав языковую игру, иначе вопрос не имеет смысла.
Я понял. Я так не считаю. Я считаю, что у математического знания есть 2 критерия полезности:
1) Полезность для прикладных наук.
2) Возможность сделать человечество умнее. Под "умнее" я понимаю способность в каких-то контекстах отличать истинные утверждения от ложных. Инструментарий, который позволяет это делать (пусть и не всегда), отличает науку от пустой пиздоболии (сейчас набегут мамкины феласафы и скажут, что математика - не наука; но я на них не буду обращать внимания). Если просто обмениваться ощущениями как в художественной литературе или эзотерике, будет, конечно, весело, но это уже будет не наука.
То есть, моя позиция такая, что когда истинность утверждений имеет меньший приоритет чем ощущения и интуиция, это уже философия, а не математика. Ничего не имею против философии, но я не хочу ей заниматься.
Я понял твою точку зрения. Но мне вот как (я очень на это надеюсь) будущему математику на полезность прикладных наук наплевать, даже наоборот - любое прикладное приложение серьезной математики так или иначе связанно с военными структурами, как показывает исторический опыт.
>. Под "умнее" я понимаю способность в каких-то контекстах отличать истинные утверждения от ложных.
Ну, истинность в математике - это ведь относительное понятие. Утверждение не может быть истинным само по себе, оно истинно только в контексте той или иной теории (говоря чуть строже, в той или иной модели конкретной теории) - и это то, чему учит нас мат. логика (по крайней мере наивная). То есть даже аксиомы логики - это не нечто, данное свыше и выделенное, это нечто, что мы сами для себя придумали, и что может поменяться уже завтра, если внезапно поменяется мода в математическом мейнстриме. Поэтому мы максимум можем научить человека понимать, что из данных аксиом при данных правилах вывода можно получить данные утверждения - что уже гораздо менее круто и непонятно, где это может пригодится (он это максимум что может использовать как метафору при построении "жизненных рассуждений" - а это как раз таки гуманитарный аспект математики).
Я вот не мамкин феласаф, но я вот всерьез не считаю математику полноценной наукой - это некоторый совершенно иной род деятельности. Она просто организована как наука - научные журнальчики, кафедры всякие, но там гораздо больше свободы, чем в науке. Математик (в широком смысле) может "убить" неприятные ему эффекты сменой определений, физик же не может игнорировать результаты эксперимента просто поменяв пару слов. Поэтому в математике идут всегда два процесса исследование уже построенного унивёрсума (научная часть) и переформирование и создание новых унивёрсумов ("эзотерическая" часть, неспецифичная ни для какой другой науки).
> даже наоборот - любое прикладное приложение серьезной математики так или иначе связанно с военными структурами, как показывает исторический опыт.
Напомнило вот это интервью
http://trv-science.ru/2016/02/23/o-bublikah-babushkah-i-korrektiruyushchikh-kodah/
> В возрасте лет 17, когда надо было выбирать направление, у меня было такое соображение: мне бы хотелось заниматься чем-то, что приносило бы пользу человечеству и при этом не приносило пользу советской власти. Математика идеально удовлетворяла этим условиям.
> Утверждение не может быть истинным само по себе, оно истинно только в контексте той или иной теории
Согласен. Но в контексте теории, в которой мы работаем, процент ошибочных утверждений должен быть явно меньше 50-70, это уж слишком, на мой взгляд.
> То есть даже аксиомы логики - это не нечто, данное свыше и выделенное, это нечто, что мы сами для себя придумали, и что может поменяться уже завтра, если внезапно поменяется мода в математическом мейнстриме
Во-первых, скорее всего, если их придется изменить, то можно будет отделаться "малой кровью", то есть действительно ценные (прости, что не зафиксировал языковую игру) утверждения останутся верными; быть может, с небольшими изменениями.
Во-вторых, даже если считать, что вполне реальна ситуация, когда от всей математики откажутся и найдут ей замену, нет оснований пренебрегать истинностью утверждений. Это как никогда не мыться, потому что все равно потом испачкаешься.
>То есть, моя позиция такая, что когда истинность утверждений имеет меньший приоритет чем ощущения и интуиция, это уже философия, а не математика. Ничего не имею против философии, но я не хочу ей заниматься.
«Истинность» — это специфическое понятие некоторых логиков и педагогов. В математике оно используется достаточно редко, в качестве грубой модели сложной картины взаимосвязей. В физике и тем более инженерии, где нужно реально что-то делать, истинность в миллион раз важнее, чем в математике. От того, что великая теорема Ферма верна никому ни холодно, ни жарко. Философия тут вообще ни при чём. Доказательство, которое не может понять человек никому не нужно, это просто куча символов.
Определения, теоремы, доказательства — разделение, основанное непонятно на чём кстати. По-моему оно вовсе не является вшитым в глубинную структуру. Само существование математики — факт, до сих пор не объяснённый (как существование жизни).
Как геометрически представить себе тензор? Алгебраически более-менее понятно.
Откуда взялось слово «тензор»?
Откуда взялось слово «тензор»?
>Аноны, а откудавзялось слово круг? Ну геометрически что такое круг более менее понятно, но почему слово круг не круглое?
Спасибо.
Бля, анончики, ну вы не гоните так на аксиоматический метод. У меня манямирок рушится же. Я теперь спать не смогу.
Аксиоматический метод — изобретение пары поехавших греков, обстёбанное студенческой группой «Бурбаки», а так же средство дрессировки быдла в школах и универах, здоровый человек не может без отвращения смотреть на это недоразумение.
категорное мышление ведь на дворе, категорную мышцу разрабатывай!
Ты пытаешься вытащить себя из болота за свои собственные волосы.
Чисто технически это возможно, что то там про импульс и про неравномерность трения на разных скоростях, но для этого не хватает сил которыми обладает человеческая рука.
>Доказательство, которое не может понять человек никому не нужно, это просто куча символов.
И тут ты такой определишь "понять". Для тебя это видно нечто вроде вскрика "эврика", когда все становится ясно, однако, это субъективное восприятие понимания.
Ну субъективное, и чего?
Чувак, хуёвая идея. Просто хуёвая. Лучше просто уходи сам.
Понятие «определения» по иерархии ниже (не очевидно, что выше) понятия «понимания», поэтому «определение понимания» бессмысленнно (не факт, что должно (может) иметь смысл).
Так как ты можешь говорить о вещи, которую не описал? Вот предположим кто-то вдруг утверждает, что понял доказательство абц-гипотезы. И как мы его проверим?
>Напомнило вот это интервью
Единственное, что в Мише Гельфанде есть от математика -- это фамилия, если что.
Самому понять доказательство и посмотреть. Проверять, что кто-то что-то понял самому не понимая — достаточно специфическая деятельность. Если её поймёт много людей это можно будет увидеть как обычно, по социальным признакам.
Только сказанное не отменяет таинство понимания, что по мне совершенно недопустимо. Лично я не вижу никаких отличий человеческого понимания от понимания пруф ассистанта, помимо того, что у человека присутствует инсайт.
По какой иерархии? Откуда ты взял эту структуру?
А также образование на мехмате и учёная степень. Он кандидат физико-математических наук.
>Только сказанное не отменяет таинство понимания, что по мне совершенно недопустимо.
Шагом по направлению к пониманию понимания будет разве что создание сильного ИИ (а не ебучих пруверов, которых для этой цели явно недостаточно).
>Лично я не вижу никаких отличий человеческого понимания от понимания пруф ассистанта, помимо того, что у человека присутствует инсайт.
Что за «инсайт»?
Лично я не вижу никаких отличий между компьютером и камнем, помимо того, что у компьютера присутствуют некие мелкозернистые паттерны.
https://en.wikipedia.org/wiki/Insight
Разговор же шел о понимании доказательств теорем, а не о их нахождении. Так вот я не могу понять, что же есть такого в понимании, помимо осознания того, что все преобразования в соответствующей системе верны (работа пруфассистанта)?
Интервью не с ним же.
Защищался он уже на тему информатики, но интервью и правда не с ним, проглядел.
Где найти PDF-книгу новую Бурбаки? Не знает никто? Хотя бы на французском.
Алгебраическая топология, с няшными категориями!
Алгебраическая топология, с няшными категориями!
Да ты охуел! Читай список из ОП-поста и не возникай. Люди для тебя старались, книжки писали, а тебе бурбаки на французском подавай! Самому-то не стыдно?
Она уже есть в библиотеке любого приличного ВУЗа.
в саранском политехе нету
Эрго, сранский политех - не приличный вуз.
Так я же сказал, мне PDF нужна. Я же не говноед, чтобы бумажное читать.
Но Бурбаки тоже старался!
Начал читать Reid, Geometry and Topology. Поясните за определение пикрелейтед. По-моему, глупость какая-то. Разве в евклидовом пространстве не должно быть задано скалярное произведение, так как в нем есть углы?
Или геометрия по дефолту такая уебищная и нестрогая?
Книжка плохая.
Пробовал Прасолова читать, так там я вообще блеванул от стиля изложения.
Ты чё, ебан?! Перечитай ещё раз. Где ты видишь нестрогость, а? Типичный двачер нахуй.
E^n -- это метрическое пространство, изометричное R^n. Что тебе нахуй непонятно здесь? Скалярное произведение при желании ты можешь ввести через изометрию, причем от выбора изометрии оно не зависит.
Сучка ты такая, какого хуя ты выёбываешься на нормальное определение, а?
А что с ним не так?
Т. е. ты хочешь сказать, что любое пространство изометричное R^n имеет скалярное произведение <x, y> = \sum_{i=1}^n x_iy_i ? Во-первых, что-то не верится. Во-вторых, если это так, то схуяли об этом ни слова не написано в книге?
Да, скалярное произведение _векторов_ не будет зависеть от выбора изометрии.
Т. е. будет сохранено <A - B, C - B>, а не <x, y>.
Просто смысл евклидовых пространств именно в том, что нет выделенной точки, все точки равноправны.
Ну и как доказать? В книге ничего не написано. У меня нет идей. Ну, допустим, норма индуцируется метрикой как |v| = d(v, 0). А как скалярное произведение получить из нормы или метрики?
Блеа, вы тут о чем угодно готовы спорить. Является ли множество Мандельброта локально связным? Дискурс.
Охуенно понравилась книга Пойа, о правдоподобных рассуждениях. Особенно первая главаЮ она же и единственная пока что мной прочитанная. Прямо вкусно читать
Скалярное произведение двух векторов полностью определяется их длинами и длинами проекций одного на другой. Длины изометрия сохраняет, прямые сохраняет, проекция точки на прямую -- это ближайшая точка на прямой, то есть определяется через длины и прямые -> тоже сохраняется. Выходит, сохраняется и скалярное произведение любых двух векторов.
Видеозаписи лекций Сергея Иванова по геометрии и топологии хороши.
Aнон, помоги!
Посмотрел в гуглокнигах задачник по алгебре Голода, Винберга и еще кого-то. Но, увы, книга там кастрированная, а самого этого сборника я ни в интернтах в виде пдф, ни в виде простой книги не нашел. Где искать?
Посмотрел в гуглокнигах задачник по алгебре Голода, Винберга и еще кого-то. Но, увы, книга там кастрированная, а самого этого сборника я ни в интернтах в виде пдф, ни в виде простой книги не нашел. Где искать?
Аноны, я студень первого курса мехмата, впереди свободное время до конца лета. Что посоветуете почитать полезного?
gen.lib.rus.ec
Решение начинается с того, что А, В и С объявляются следующими друг за другом членами последовательности, но в условии этого не говорится. Тогда откуда это берется?
Давай еще для чистой математики, или еще для физики, чтобы я мог глянуть на СУТЬ с разныхз сторон.
Почему невозможности? Я на 5.4
Иди лучше телок клеить пока молодой. А то так и останешься девственником.
Другзадружество это сво-во элементов последовательости
> так и останешься девственником
Как что-то плохое.
Ньютон одобряет.
У меня была тян, так что я уже накутился
Ниоткуда. Задачу составлял один мудак, решал другой мудак, ты пытаешься разобраться в высере двух мудаков.
Заведи куна.
Тоже хорошее дело.
Двачуем
Там нетЪ.
И как ты определяешь проекцию без скалярного произведения?
А, все, увидел
> проекция точки на прямую -- это ближайшая точка на прямой
Я здесь только из-за гомологий уровня /b. Так-то здесь делать нечего.
>Б. М. Давидович: “Математический анализ в 57 школе“.
Я не понял, как по этому учить? Там же просто набор отдельных утверждений.
Я не понял, как по этому учить? Там же просто набор отдельных утверждений.
FGJ, это смысл афинных пространств, смысл евклидовых пространств как раз в том, что это векторные пространства с фиксированным скалярным произведением.
А хули он девственник, норм же ебальник, патлатый роцкер такой
Мог себе позволить
Лол. Нет. Аффинное пространство -- это если убрать ещё и длины, и углы, а не только выделенную точку. Евклидово -- когда убирают именно точку.
>A Euclidean space is not technically a vector space but rather an affine space, on which a vector space acts by translations, or, conversely, a Euclidean vector is the difference (displacement) in an ordered pair of points, not a single point. Intuitively, the distinction says merely that there is no canonical choice of where the origin should go in the space, because it can be translated anywhere. When a certain point is chosen, it can be declared the origin and subsequent calculations may ignore the difference between a point and its coordinate vector, as said above. See point–vector distinction for details.
Я тоже могу, я как Ньютон да?
Ну в разных учебниках по разному.
Ну, тащем-то особой разницы и нет на самом деле, всё равно все евклидовые это R^n-ки, а само понятие устарело, как и всякие аксиоматически заданные геометрии.
Ну тут такое. в 95% случаев достаточно работать с R^n, но часто бывает, но бывают случаи, когда лучше работать с абстрактным n-мерным евклидовым пространством, у которого нет какого-то естественного ортонормированного базиса (который есть у R^n).
x = 2
решить для всех х
решить для всех х
корень ^z из x ^ n ( n = z) n,z mod 2 = 0, x принадлежит {2}
Посоны, давайте макаку пинать чтобы он латекс или какой-нибудь аналог запилил хотя бы на эту доску, для эксперимента. Очень тяжело формулы писать.
Может модер на связь выйдет и через него просьбу передать получится?
Может модер на связь выйдет и через него просьбу передать получится?
Если это осознанный выбор.
нахуя, тут формул никто не пишет
Постоянно пишут. Пытаются, по крайней мере. Астериск макаба постоянно теряет, очень не хватает дробей, стрелочек, кванторов, математического языка, в общем.
Уже просили дохуя раз. Макаке поебать на sci, с него ведь траффика 0.
Поэтому его нужно регулярно доебывать. Не все же на свете упирается в трафик. Все-таки здесь островок высокого в море мелочных интересов и развлечений.
Нужно своя мелко-борда. С дробями, графиками и категориями.
А вместо капчи гамалогии.
Увожаемый, вы про интегралы забыли!
Да нет, вроде не забыл ни о чём таком ещё математическом.
Взял интеграл? Положи его на место, блядь!
> Очень тяжело формулы писать.
Прикрепляй в виде картинок.
Эти как-то не очень с виду. А Тьюринга я б сводил в кафе и на синематограф. Он ещё и спортсмен был...
Почему в шапке нет дискретки, тервера и матстата? Здесь их не уважают?
Иди нахуй, вырожденец.
Алсо, из шапки необходимо также весь Real Analysis и Calculus нахуй убрать. Просто нахуй.
Тапалогия-дебил порвался, найс. Пока не сможешь брать хотя бы тройные интегралы от топологии руки прочь!
Двачую. А заодно дифференциальную и симплектическую геометрию, геометрическую и комбинаторную теорию групп, геометрический анализ и прочее второкультурное говно с вашими динамическими системами и теориями струн.
Математика, блядь, это Гротендик, Квиллен, Делинь, Мамфорд, Воеводский, Тоен. А Вербицкие и прочие говноеды Каледины идут нахуй.
>топология
Общая топология тоже второкультурное говно, уточняй что имел в виду, собака.
>геометрическую теорию групп
Пашёл нахуй. Громов концептуален.
>собака.
Гротендик твой собака!
Интегралы важнее любой 'первой кулькуты' хотя бы потому что имеют важную прикладную роль.
Уже после их изучения надо остальное учить!
Громов второкультурщик и это очевидно. Концепции бывают разные. Конвей тоже концептуален, Кокстер. Есть чистая математика, и она только в Гарварде. А дифференциальное-геометрическое и прочее околофизическое говно в Принстоне и в других местах.
Вторая культура скрывается везде. Даже изучая алгебраическую геометрию у тебя может возникнуть соблазн перейти от рассмотрения категории схем к свойствам конкретной схемы, а там уже до теории струн не далеко.
Интегралы изучаются в курсе калькулюса на многообразиях, вместе с теорией меры, метрической геометрией и общей топологией. Нужно это только второкультурщикам, прикладникам, инженерам, геологам и прочим далеким от математики людям. И еще вопрос, нужно ли.
Разве не у каждой математической теории есть применения в реальности?
Чистая математика не применяется к реальности, она открывает её. Бесконечное количество этих реальностей. Если подумать, это гораздо круче, чем изучать то, что имеется в действительности. Ведь человек всю историю пытается узнать что-то о мире, в котором он живет. И очевидно, что это знание всегда будет не полным. А занимаясь чистой математикой он выходит далеко за пределы всего физически существующего.
Ты шизоид?
У тебя просто узкое мышление слишком, в математику таким противопоказано. Занимайся физикой, изучай соответствующую математику трехсотлетней давности. Твое мышление застряло в конце 18-го века вместе с наивным позитивизмом, атеизмом и сциентизмом.
Каждый настоящий математик обязан быть мистиком и изучать санскрит как Андре Вейль, например. Хотя и не обязан быть упоротым структуралистом при этом.
Очень аргументированно. К ЕГЭ уже готовишься?
Тут нечего аргументировать. Он тебе все правильно сказал. Дискретная математика, тервер и прочее это на факультете статистики. К математике имеет такое же отношение, как машиностроение или геофизика.
С чего это вдруг он обязан быть мистиком? По твоему каждая тупая пизда изучающая эзотерику, колдоство и подобную муть может стать настоящим математиком?
Да и физики больше в эзотерику удоряются, чем математики, взять хотябы Рыбникова, он физик по образованию.
Сосач такой сосач.
>По твоему каждая тупая пизда изучающая эзотерику, колдоство и подобную муть может стать настоящим математиком?
Да уж. Полное отсутствие логики и путаница причины-следствия, тебе явно не в этот тредж.
Забавные вы тут детишки.
Но ведь это именно ты путаешь. Верун в мат-треде, лол.
Господин первокультурщик, а что из алгебры современной первая культура, не подскажите?
Находение корней уравнений. В C или H.
Что общего имеет скажем Воеводский с тупой пиздой, изучающий эзотерику и колдовство? В любой области деятельности есть профаны и неофиты, и в науке и в теологии. Достаточно давно обсуждается вопрос о том, чем математика является, а чем нет. Арнольд, например, считал что математика является частью физики и его школа развивала соответствующую математику, выше описанную мной как "второкультурное говно". Есть мнение, что математика сочетает в себе различные взгляды и подходы но в целом больше походит на мистическое учение, выходящее за пределы традиционных представлений, навязанных христианством и философией Аристотеля (на которых построен рационализм, по сути). Соответственно здесь хорошо зайдет восточная философия. Если не можешь читать Гротендика, об этом много есть у Воеводского, или совсем популярно, у Ромы Михайлова.
Что такое логика? Существует мнение, что это отдельная наука или по крайней мере дисциплина, предмет изучения. Откуда взялось такое мнение? Из философии Аристотеля, внезапно. Многие даже относят "математическую логику" к разделу этой "логики". Хотя очевидно, что математическая логика, более корректное название "метаматематика" это споры о том, что корректно или допустимо в самой математике, например там теория множеств Кантора является допустимой, или аксиома выбора, или закон исключенного третьего. "Логика" в данном случае не более чем прилагательное. Типа "А какая у ваших рассуждений логика?".
A1-Homotopy theory of schemes, homotopical algebra, derived algebraic geometry, universal cohomology, mixed motives & Voevodsky conjecture, étale k-theory.
Дух треда проснулся.
> Calculus нахуй убрать. Просто нахуй.
Ну это и так всем нормальным людям очевидно.
> Real Analysis убрать
Дурачек что ли? Real Analysis - это такая солянка из очень разных областей, где доказывают теоремы, а не интегральчики берут. Причем там изучаются совсем основы. Вот из этих тем назови хотя бы одну, которую математику можно не знать:
1) Топологические пространства. Непрерывность, связность, компактность. Метрические пространства. Фундаментальные последовательности, полнота, пополнение.
2) Определение поля вещественных чисел. Поле комплексных числе.
3) Определение пространства с мерой. Интеграл Лебега. Произведение мер, теорема Фубини.
4) Дифференцирование. Производные Фреше и Гато, теорема о неявной функции, теорема об обратной функции. Классы гладкости, определение диффеоморфизма. Фундаметальная теорема матана, формула Ньютона-Лейбница, Якобиан и замена переменных в интеграле.
5) Ряд Тейлора. Аналитические функции.
6) Пространство непрерывных ограниченных функций, равномерная сходимость. Признак сходимости числового ряда через корень n-й степени. Радиус сходимости степенного ряда. Обоснование почленного интегрирования и дифференцирования рядов.
Определение функций exp, sin и cos.
7) Теорема Арцела-Асколи и теорема о существовании и единственности решения ОДУ.
Часто еще в курсе Real Analysis изучают дифференциальные формы и теорему Стокса, но, это, наверное, правильнее отнести к анализу на многообразиях.
Я еще очень много чего не написал. Но это просто пример тем, которые изучаются в курсе Real Analysis. Ясно, что нет ни одного нормального математика, который мог бы не знать хоть чего-то из того, что я перечислил.
>Ну это и так всем нормальным людям очевидно.
При этом практически все что ты перечислил, относится к calculus'у. Кроме теории меры. Calculus (on manifolds) — предваряющая дифференциальную геометрию дисциплина. Дифференциальные формы, формула Стокса, производные Ли и тд. Калькулюс — мат. аппарат физики (теории относительности и электромагнитной теории).
Analysis это то, что в России называют функциональным анализом. То есть дисциплина, продолжающая общую топологию. То есть метрические пространства со структурой меры. Lp spaces, Hardy space, спектральная теория и прочее. Большинство математиков там даже не поймут о чем речь, настолько это нахуй не надо.
Большинство этих тем не нужны математикам, а нужны физикам. А те, которые всё-таки нужны, приличными математиками должны изучаться в отдельных курсах.
Например, поле комп. чисел в курсе топологии поля C (по типу Бурбаки).
С остального вообще проиграл.
Пиздец ты бля ебанутый нахуй. Много реальностей наверное открыл, открыватель.
Говорю же он шизоид.
Каждый математик обязан быть шизоидом в том смысле, который ты вкладываешь в это понятие.
Математика это и есть реальность. Единственная и объективная.
Шизодид - это даже не оскорбление, блядь. Это совсем далеко от шизофрении, ебанат.
Не надо проэецировать на других свои маня-фантазии.
Я и не называл его шизиком.
> Lp spaces
> спектральная теория
> нахуй не надо
Ясн))0
> А те, которые всё-таки нужны, приличными математиками должны изучаться в отдельных курсах.
Невозможно, потому что они ссылаются друг на друга. Я же написал темы не в таком порядке, в каком их надо изучать, а от более фундаментальных концепций к менее фундаментальным.
> Например, поле комп. чисел в курсе топологии поля C
Ага, а все результаты, которые одинаковые для R и C ты по 2 раза будешь доказывать? Или ты считаешь нормальной ситуацию, когда, например, первокурсник не знает даже формулу Эйлера? Короче, ты слишком даун даже для вербитодауна. Вербит-то наверняка еще в 8 классе знал все то, что я перечислил, несмотря на то, насколько сильно он хэйтит матан.
Скорее попытка понять реальность на обобщенном и абстрактом в отличие от физики уровне.
Я к тому, что все открытия математиков рано или поздно находят реализацию в реальном мире и осваиваются другими науками. Иначе в ней бы не было смысла.
Я не проэецирую, а говорю за современную математику. Можешь заниматься говном трехсотлетней давности и дальше, брать интегралы методом подстановки преобразования подыинтегрального выражения и думать, что алгебраические уравнения выше пятой степени не решаются в явном виде.
>Ага, а все результаты, которые одинаковые для R и C ты по 2 раза будешь доказывать
Поэтому адекватные люди излагают математику для произвольных полей сразу. Есть еще p-адический анализ, например. R^1 или даже R^n для даунов.
>насколько сильно он хэйтит матан.
Не хейтит вообще, у него есть курс лекций по метрической геометрии и по теории меры. Две книги, около 400 и 150 страниц соответственно, с большой любовью написаны.
Полная хуйня. Смотри, в физике (теории струн) ты смотришь на вселенную как на многообразие. При этом элементарные частицы это морфизмы между расслоениями. В математике ты работаешь с категорией многообразий. То есть это все возможные вселенные вообще, а не только одна существующая. Чувствуешь расстояние, мудило?
Ну да прикинь в пирожковой ты работаешь с пирожками 1 пирожок, 2 пирожка n пирожков, а в математике с числами, которые могут быть приложены к любым объектам, которые могут быть посчитаны, то - есть находятся некие общие закономерности существующей реальности, а затем они приспосабливаются к частностям. Но это закономерности не придумали математики, они уже существовали, просто их обнаружили и все и математика не изобретает реальность, а находит в ней взаимосвязи.
>наука о структурах, порядке и отношениях
Не спорь с википедией.
Математика - это полное всё, абсолютно точное и объективное. Физика - просто неумелое, вызывающее жалость, приближение к этому всему.
Ну да и без физике ты бы сидел в пещере, мы то живем не в абстрактом маня мире. А спорить о том, какая наука круче - вообще детский сад.
физики*
fixed
Нет понятий "круче" - когда приходишь со своего завода, старайся оставлять все свои определения там же.
Но есть понятие истинности.
Аргументы же, будто бы мы сейчас сидели в пещере, если бы не физика, - уж точно "детский сад". От незнания, по-видимому.
Давай, ты убьёшь себя?
>Но есть понятие истинности
Есть, но для каждого утверждения вида "x истинно" всегда найдется в не меньшей степени подкрепленное и убедительное утверждение "x ложно". Называется это релятивизм. А то, о чем ты говоришь, называется "идеализм". В математике это решается переходом к другой системе аксиом. Говорить об абсолютной истинности это уже не "завод", и не "детский сад", а секта какая-то с элементами агрессии. Вот уже желаешь смерти людям, имеющим мнение отличное от твоего.
>A1-Homotopy theory of schemes, homotopical algebra, derived algebraic geometry, universal cohomology, mixed motives & Voevodsky conjecture, étale k-theory.
А, алгемчик, ясно.
Алгем методами алтопа скорее.
>То есть это все возможные вселенные вообще, а не только одна существующая.
Ну так ты и от своего многообразия-вселенной можешь взять кусок, и получится другое многообразие.
> Поэтому адекватные люди излагают математику для произвольных полей сразу.
Во-первых, ты пиздишь. Сам-то ты не так математику изучал. Даже, наверняка, сначала изучил всякие интегральчики под картофан, а потом только узнал, что, оказывается, вещественные числа образуют поле.
Во-вторых, R - это полное (в топологическом смысле) упорядоченное поле. R - единственное (с точностью до изоморфизма) с такой топологической и алгебраической структурой.
Чо-чо-чо. Для анализа достаточно чтобы в поле сходились фундаментальные последовательности, такое пространство называют метрически полным.
В p-адических числах они тоже сходятся, не только в R. R просто один неудачный пример поля, при чем еще не замкнутого алгебраически. Хуй знает что к нему привязались, ебанаты. И да, в p-адических числах корни вычислять тоже можно.
> Чо-чо-чо. Для анализа достаточно чтобы в поле сходились фундаментальные последовательности
Нет. Без R ты не сможешь даже сформулировать определение метрического пространства. Потому что метрика показывает насколько близко/далеко точки находятся друг от друга. То есть в качестве codomain у метрики обязательно должно быть упорядоченное поле.
Че непонятного? Открываем википедию
https://en.wikipedia.org/wiki/Ordered_field
> Any Dedekind-complete ordered field is isomorphic to the real numbers
Dedekind-complete означает, что у поля есть least-upper-bound property, т. е. что у ограниченного сверху множества есть sup.
Поэтому R уникально и без него можно только сосать хуй.
Или метрические пространства тоже для даунов? Всего лишь частный случай топологических пространств.
>Нет. Без R ты не сможешь даже сформулировать определение метрического пространства
Для определения метрического пространства мне достаточно задать расстояние, оно может быть нулевым, расстояние от x до y равно расстоянию от y до x, неравенство треугольника. При чем тут R? С чего ты взял, что только R является упорядоченным полем? Q не является? Пруфы?
>Dedekind-complete означает, что у поля есть least-upper-bound property,
Отсюда никак не следует, что анализ нельзя строить над полем, которое не является полным по Дедекинду. Qp не является полным, но над ним уже давно построили.
Точнее является полным, но как раз в метрическом смысле, метрика порождается p-адической нормой.
Навыдумывают себе условий, делающих R уникальным и гордятся.
> Собирается определить метрику как функцию со значениями в Q.
Ну ты просто эпик даун, если не видишь, с какими проблемами ты при этом столкнешься. Не овладел простейшими концепциями уровня 1 курса вроде пополнения метрического пространства и least upper bound property, но выучил модные баззворды и кудахчешь КО-КО-КО МОРФИЗМЫ МЕЖДУ РАССЛОЕНИЯМИ КУДАХ-ТАХ-ТАХ))0 ВЕЩЕСТВЕННЫЕ ЧИСЛА НЕ ВОЗНИКАЮТ В ЧИСТО АЛГЕБРАИЧЕСКОЙ СИТУАЦИИ, А ВСЕ ЧТО НИ АЛГЕБРА ЭТА КАРТОФАН ЕБАНЫЙ КАРОЧ))0 ВСЯ ФУНДАМЕНТАЛЬНАЯ МАТЕМАТИКА - ЭТО АЛГЕБРА И ТЕОРИЯ КАТЕГОРИЙ, А ОСТАЛЬНОЕ - ПЕРИФЕРИЯ ДЛЯ НЕГРОВ))0
>вроде пополнения метрического пространства
Давай поменьше пизди. Qp — такое же пополнение Q, как и R, тоже локально компактное полное по метрике, порожденной p-адической нормой.
>least upper bound property
Не вижу почему меня это должно интересовать в данной ситуации
> >least upper bound property
> Не вижу почему меня это должно интересовать в данной ситуации
1) Определи мне расстояние от точки до множества в метрическом пространстве.
2) Обоснуй существование корня n-й степени из любого положительного (еще придумай, что значит "положительное" в произвольном поле, если это не R или Q) числа.
Короче, все, после этого можешь сразу идти нахуй
> >least upper bound property
> Не вижу почему меня это должно интересовать в данной ситуации
Ты же реально программу 1 курса не знаешь, это просто позорище. Пиздуй читать учебник по матану, какие тебе расслоения.
Как ты думаешь, почему метрика принимает значения именно в R, а не в произвольном упорядоченном моноиде?
>существование корня n-й степени из любого положительного
Для чего тебе корень из любого числа? Корни извлекать можно, доказывается это леммой Гензеля, правда в данном конкретном расширении у какого-то числа может не быть корня, не вижу никакой проблемы в этом. Кроме того, и в действительных числах ты для любого числа можешь только построить корень геометрически — то есть указать точку, в которой он находится, но не получить численное значение.
Алсо, можно построить p-адический аналог комплексных чисел и p-адические степенные ряды.
>Ты же реально программу 1 курса не знаешь
Так я и не учусь на первом курсе. А ты недавно закончил, судя по всему.
>произвольном упорядоченном моноиде?
Потому что в произвольном упорядоченном моноиде не все элементы обратимы? Что за вопросы вообще?
Эй, волшебник-эзотерик, как ты относишься к пруф ассистентам? Готов пилить свою математику в проверяемом виде или готов мириться с неверностью / неверностью доказательств половины маня-выводов?
Как к ним можно относиться? За ними будущее.
Какое будущее, лол? Ты или уже пилишь проверяемые док-ва, или пилишь новые ассистенты, или сосёшь хуй. Третьего не дано.
Как насчет аксиомы выбора, кстати?
Не ведитесь на маркетологические визги этого модника.
Ты про эзотерика?
Да.
Я на него и не ведусь. Как он начал втирать про то, что КАЖДЫЙ математик должен быть эзотериком, я понял, что он залётная манька.
>Как насчет аксиомы выбора
Она попросту неверна уже для топоса Гротендика, это давно известно.
Ты чё, ебан что ли?
>неверна
Значение знаешь?
Аксиома выбора нарушается более-менее в любом топосе Гротендика.
Простейший геометрический пример: топос пучков множеств на окружности.
Категория множеств в данном случае — категория этальных накрытий
окружности.
Соответственно, легко построить пример, в котором будет нарушаться
даже слабейшая форма аксиомы выбора.
Например, рассмотрим связное двулистное накрытие окружности
и его отображение в однолистное накрытие.
Это эпиморфизм (= сюръекция) множеств.
Но у этой сюръекции нет сечения.
Так что если вы хотите делать алгебраическую геометрию в семействах
(например, на той же окружности)
(а Гротендик многократно подчёркивал, что именно в семействах и надо её делать)
то от аксиомы выбора придётся отказаться.
А в каком-то нормальном месте и желательно на английском я смогу это прочитать?
В блоге Тоёна.
>Например, рассмотрим связное двулистное накрытие окружности
и его отображение в однолистное накрытие.
>Это эпиморфизм (= сюръекция) множеств.
>Но у этой сюръекции нет сечения.
Ну и бред же я только что прочитал) И где здесь нарушается аксиома выбора, м?
>Это эпиморфизм (= сюръекция) множеств.
>Но у этой сюръекции нет сечения.
Почему нет?
Блядь поясните за бред про накрытия, который шизотерик снёс?! И где говно-блог этого Тоена? И ещё никто эту хуету на mathoverflow не обсуждал.
Сука, как пичот с этого "знатока"
Сука, как пичот с этого "знатока"
ВИНБЕРГ ИЛИ КОСТРИНКИН???
1. Винберг/М. Артин
2. Варден/Зейферт
3. Маклейн/Алуффи
Фундаментальные наброски концепций, оформленных в виде мало-риторических вопросов и элементарных рассуждений:
Во-первых, что людское сознание мета-подразумевает под качествами объекта, традиционно математическими - например, что мета-подразумевается под площадью?
В математике площадь объекта напрямую не связана больше ни с какими другими свойствами этого объекта, то есть, если площадь объекта равна значению Z, это, естественно, не несёт информации, например, о форме объекта. Таким образом математическая модель любого вида - просто набор бессвязных между собой огрызков.
Наша же новая наука должна создать возможность построить связанную по своей внутренней структуре модель всего объекта, и его, снова приводя пример, площадь будет лишь срезом этой модели; площадь будет содержать так называемые "ссылки" на информацию о других свойствах нашего объекта, ссылки, которые будут сами заложены в концепции и площади, и самого объекта! То будут потоки данных, активно изменяющиеся и влияющие друг на друга. Грубо говоря, по типу того, как Эйнштейновские уравнения переходят на нерелятивистских скоростях в ньютоновские, наша общая модель объекта при преобразованиях будет переходить в конкретное значение, например, площади объекта. Эта концепция ключевая.
Во-вторых, нужно продолжить говорить более конкретно: что же есть площадь и что она должна показывать? Меру развёрнутости объекта в пространстве? (таким образом, вообще говоря, сразу же налаживается первый мост - площадь должна иметь конкретные "ссылки" на структуру пространства, в котором она рассматривается, то есть, учитывать всю его метафизическую структуру).
В-третьих, наша новая наука должна иметь непосредственную связь с реальным всё - таким образом за фундаментальную единицу можно будет принять Планковскую длину, а также отказаться от концепции бесконечно малых, бесконечности в целом.
Это первые мысли. Они незрелые. Начальные.
Le Place.
Во-первых, что людское сознание мета-подразумевает под качествами объекта, традиционно математическими - например, что мета-подразумевается под площадью?
В математике площадь объекта напрямую не связана больше ни с какими другими свойствами этого объекта, то есть, если площадь объекта равна значению Z, это, естественно, не несёт информации, например, о форме объекта. Таким образом математическая модель любого вида - просто набор бессвязных между собой огрызков.
Наша же новая наука должна создать возможность построить связанную по своей внутренней структуре модель всего объекта, и его, снова приводя пример, площадь будет лишь срезом этой модели; площадь будет содержать так называемые "ссылки" на информацию о других свойствах нашего объекта, ссылки, которые будут сами заложены в концепции и площади, и самого объекта! То будут потоки данных, активно изменяющиеся и влияющие друг на друга. Грубо говоря, по типу того, как Эйнштейновские уравнения переходят на нерелятивистских скоростях в ньютоновские, наша общая модель объекта при преобразованиях будет переходить в конкретное значение, например, площади объекта. Эта концепция ключевая.
Во-вторых, нужно продолжить говорить более конкретно: что же есть площадь и что она должна показывать? Меру развёрнутости объекта в пространстве? (таким образом, вообще говоря, сразу же налаживается первый мост - площадь должна иметь конкретные "ссылки" на структуру пространства, в котором она рассматривается, то есть, учитывать всю его метафизическую структуру).
В-третьих, наша новая наука должна иметь непосредственную связь с реальным всё - таким образом за фундаментальную единицу можно будет принять Планковскую длину, а также отказаться от концепции бесконечно малых, бесконечности в целом.
Это первые мысли. Они незрелые. Начальные.
Le Place.
Что?
>мета-подразумевается под площадью?
Теория меры.
>отказаться от концепции бесконечно малых,
Интуиционизм, конструктивизм.
Пока не прочитаешь Воеводского, не приходи.
Ответил на твой вопрос, дебил, блядь. Онищик-Зуланке. Шафаревич. Дьедонне. Маклейн-Биркгоф. Ленг. Городенцев. Вавилов.
Сначала изучаешь коммутативную алгебру, потом комплексный анализ, потом гомологическую алгебру, потом пучки, потом алгебраическую к-теорию.
>Теория меры.
Ебать, ты мудак? Я говорю об отказе от этого, тупой проблядок отвечает мне на это очередной мат. теорией. Сгинь в /re.
Теория это просто название, успокойся. Типа "А какая в ваших рассуждениях теория". Все, что самостоятельно изобрел Гротендик, священно и отказываться от него нельзя.
>Категория множеств в данном случае — категория этальных накрытий
окружности.
ЕБАН. Показал какую-то совершенно левую категорию нихуя не множеств, и сообщаешь блядь что переформулировка аксиомы выбора там не работает. Пиздец нахуй.
Блядь ты уебок. Это и есть утверждение. Для этальных накрытий аксиома выбора неверна, ничего другого тут не утверждается. Тупой даун блядь.
Блядь это просто не аксиома выбора, это совершенно левое утверждение, более сильное, чем она.
>Она попросту неверна уже для топоса Гротендика
Уйблядь вот это даун ебучий. "уже для". Ага.
С хуя ли более сильное? Менее.
И тут ты такой показываешь, как из неё следует обычная аксиома выбора. А я ржу над твоим долбоебизмом.
*блядь, как из обычной аксиомы выбора следует она
Почему пока читаешь то все понятно и лохично, а если пытаешься решить примерчик, то обсираешься? Откуда вообще эта иллюзия знания и понимания? Как это обьясняет эвлюционная психология? Неужели наших предков не убивали хищники изза того, что она не смогли найти дискриминант или открыть скобки?
Кстати, да. Тоже этого не понимаю.
>Откуда вообще эта иллюзия знания и понимания?
Ты же на дваче, лол. Подрастёшь - иллюзия исчезнет. Правда, некоторые её на всю жизнь сохраняют.
Ты даун, что ли?
Забавный эффект, психологи изучали.
Мозг путает узнавание с пониманием. Так что чтобы проверить, понял ли ты, нужно обязательно что-нибудь решить.
Нет. А ты - малолетний уебан.
В чем суть обратных функций? Почему их в учебнеики пихают?
Но из чего следует, что величины углов треугольника единственные члены последовательности? Последовательность ведь может состоять из хуй пойми скольки элементов. Об этом в условии не сказано.
Хз, было сказано, что эта задача была во вступительных по матеше в самый престижный хиндустанский вуз.
> мудаки
> пиндостанский вуз
Так всё так.
Не могу я поверить в индукцию. Сил нету уже. НЕ МО ГУ.
Вот врёти, и все тут.
Вот врёти, и все тут.
Ну типа если ты стоишь на первой ступеньке лестнице и на какой бы ступеньке ты ни стоял, ты всегда можешь подняться на следующую, то ты можешь подняться на любую ступеньку. Вроде логично.
Алсо, я не уверен, но вроде можно объяснить индукцию через следующий принцип: "из любого непустого подмножества N можно выбрать наименьший элемент". Берем множество n таких, что P(n) не выполняется. Предположим, что оно непусто. Выберем из него наименьший элемент n. Тогда P(n - 1) верно (потому что иначе n не было бы наименьшим элементом). Значит, P(n) тоже верно. Противоречие.
Я очень сильно хочу учить и читать книжки по математики, так как в школе я пинал хуи, и математика была для меня сложна, но вот уже посмотрел 4 книжки из предложенных в ОП посте, и все для меня сложные, я не мог пройти 10 страниц потому что я не понимал о чем речь, подскажите книжку в которой все намного проще.
Ну, можешь не использовать её в своих рассуждениях.
Хорошо тут у вас, весело, не то что в другом маттреде
В каком?
ТАм анимедауны, туда я не пойду.
Прочитал учебник логики. Охуел. Мировоззрение совершило качественный скачок. Почему от меня это так долго скрывали?
Учебник психологии прочитать не забудь, ещё больше охуеешь.
ПРочитай теперь учебник по НОРМАЛЬНОЙ логике, а не по маняматической и осознай что манямаитика шкварит все до чего дотянется.
Ты чего взорвался то, когомология? Чем тебе матлогика так насолоила?
Пять хвостов на осень по математике просто у него.
БЛЯДЬ АНОНЫ У МЕНЯ БОМБИТ ОТ МОЕЙ ТУПОСТИ
Сука. есть желание понимать, изучать математику, просто по фану, но блядь не идёт.
Школьную программу знаю нормально (учился в обычной мухосранской школе, поэтому каких-то сверхпозаний в теории чисел/множеств и прочих полезных вещах нет) ну умею пересекать и объединять множества, знаю основы комбинаторики, етк. Щитать производные и легкие интегралы тож умею
Я брался за матан, сначала Зорич, застрял на 1-2 главе. Там все через множества, т.е. предполагается ты уже заебись знаешь этот раздел математики. Ладно, думаю возьму что-нибудь полегче,
скачал Фихтенгольца, и тут тоже я застрял на первых главах, где он рассказывает про дедекиндовы сечения и прочую ебань. (Само сечение понятно, уже не помню что именно вызвало ступор, читал где-то полгода назад).
И нет бы пропустить эту главу и читать себе дальше, но нихуя. Если я что-то не понял/не решил упражнение меня это жутко бесит, я не могу двигаться дальше и дропаю учебу.
Недавно искал книжку по теории множеств. Верещагин Шень "Начала теории множеств". О, думаю нормально. Около 100 страниц, упражнения есть.
Но блядь в ней уже после вводного слова автора, он предлагает порешать упражнения для самоконтроля! как на пикрелейтед.
Некоторые задачи (например 10, у меня получается решить, но нестрого, т.е. хотя бы один шаг в доказательстве я не могу доказать, хотя вроде оно и очевидно)
Или ползу на всякие dxdy или сюда, чтоб помогли решить.
Но после этого в душе остается осадок. Все равно решил не я, или хуево решил, что-то пропустил.
А если бы я сам пытался решить, то не факт что решил бы, а может потратил бы на это неделю. И когда я блять с таким темпом прочитаю хоть одну книжку?
Видимо мой предел это чтение популярных книжек для школьников, где все объясняют на пальцах.
Сука. есть желание понимать, изучать математику, просто по фану, но блядь не идёт.
Школьную программу знаю нормально (учился в обычной мухосранской школе, поэтому каких-то сверхпозаний в теории чисел/множеств и прочих полезных вещах нет) ну умею пересекать и объединять множества, знаю основы комбинаторики, етк. Щитать производные и легкие интегралы тож умею
Я брался за матан, сначала Зорич, застрял на 1-2 главе. Там все через множества, т.е. предполагается ты уже заебись знаешь этот раздел математики. Ладно, думаю возьму что-нибудь полегче,
скачал Фихтенгольца, и тут тоже я застрял на первых главах, где он рассказывает про дедекиндовы сечения и прочую ебань. (Само сечение понятно, уже не помню что именно вызвало ступор, читал где-то полгода назад).
И нет бы пропустить эту главу и читать себе дальше, но нихуя. Если я что-то не понял/не решил упражнение меня это жутко бесит, я не могу двигаться дальше и дропаю учебу.
Недавно искал книжку по теории множеств. Верещагин Шень "Начала теории множеств". О, думаю нормально. Около 100 страниц, упражнения есть.
Но блядь в ней уже после вводного слова автора, он предлагает порешать упражнения для самоконтроля! как на пикрелейтед.
Некоторые задачи (например 10, у меня получается решить, но нестрого, т.е. хотя бы один шаг в доказательстве я не могу доказать, хотя вроде оно и очевидно)
Или ползу на всякие dxdy или сюда, чтоб помогли решить.
Но после этого в душе остается осадок. Все равно решил не я, или хуево решил, что-то пропустил.
А если бы я сам пытался решить, то не факт что решил бы, а может потратил бы на это неделю. И когда я блять с таким темпом прочитаю хоть одну книжку?
Видимо мой предел это чтение популярных книжек для школьников, где все объясняют на пальцах.
> И когда я блять с таким темпом прочитаю хоть одну книжку?
Это займет часов 500 на книжку в страниц 300. Я так одну книжку прочитал (и решил > 95% упражнений), а потом понял, что это не стоило потраченного времени. С тех пор при чтении книг просматриваю все упражнения, но решаю процентов 15.
> Если я что-то не понял/не решил упражнение меня это жутко бесит, я не могу двигаться дальше и дропаю учебу.
Это пройдет, когда наработаешь математическую культуру и кругозор. Ты уже будешь осознавать, какую дичь авторы включают в качестве упражнений. В упражнения включаются не только доказательства важных утверждений, которые потребуются в дальнейшем, но и просто что-то хардкорное, чтобы у решающего жопу разорвало. Это делается потому, что учебники предназначены не для self-study, а для занятий с преподавателем, который сам может выбрать упражнения нужной степени сложности. Если кто-то начнет выебываться, что слишком легко, преподаватель даст ему гробовых задач. Вот и все.
У тебя, возможно, возник вопрос: как тогда понять, какие упражнения важные, а какие нет? Никак, это придет с опытом. Пока что можешь пытаться решать все, но пропускать, если долго не получается решить.
Это все про упражнения было. Но текста то же самое касается. Если, например, ты не особо вникая пролистал книгу вперед и уже представляешь че там дальше будет (так делать очень хорошо; я сначала не мог додуматься, что книги можно читать в несколько подходов, каждый раз с большей тщательностью), то ты можешь заранее знать, что вот такая-то теорема не нужна для получения последующих результатов, а автор ее включил, потому что посчитал ее удивительной/красивой/важной для чего-то там. Если у тебя есть желание как можно быстрее разобраться с как можно более глубоким материалом, ты можешь смело ее пропускать.
По поводу упражнений у тебя на пикрелейтед: просто нахуй их. Я тебе обещаю, если ты через несколько месяцев посмотришь на эти задачи, ты уже не вспомнишь как их решал. Можешь быть уверен на 100%, что это тебе никак не понадобится в твоей дальнейшей математической деятельности (если только ты не собираешься дрочить комбинаторику).
В общем, я тебя понимаю, у меня была в точности такая проблема. Научить себя, что не все вещи в математике одинаково ценны и интересны, научить себя отличать хорошие задачи от плохих - это очень важный навык для математика.
Так, аноны, кто может мне по хардкору объяснить, почему все числа Ферма попарно взаимно просты?
> Если я что-то не понял/не решил упражнение меня это жутко бесит, я не могу двигаться дальше и дропаю учебу.
Что будешь делать когда няша вроде Львовского хуйнет тебе в учебнике задачу Рамануджана, которую тот специально придумал чтобы потралить лалок в научном журнале и да ее никто из профессиональных математиков того времени не мог решить?
А можно скрин задачи.
1 картинка
2 картинка - бонус, из серии математики шутят
2 картинка - бонус, из серии математики шутят
> 2 картинка - бонус, из серии математики шутят
В чем проблема-то? Так как это straightforward calculation, ты можешь его сам произвести (ну или вообще забить, если ты считаешь, что совсем уж straightforward). Зачем захламлять текст?
первый математик подорвался
забей пока на книжки, наверни академию хана, начиная с арифметики https://www.youtube.com/user/KhanAcademyRussian/playlists
срань для даунов
Так ты ж подорвался. Уже полгода эту картинку постишь.
Хочу и пощу. Проблемы?
Нет проблем, просто забавляет как у тебя бомбит от неспособности произвести straightforward calculation.
Дибил, дело совсем не в этом.
Да блин, в телеге ещё хуже со степенями/сабскриптами. Формулки хуёво писать. И анонимности никакой.
Ананасы, почему пиндосские учебники по сравнению с руснявскими просто как небо и земля, как японское пирожное мендале и какой то гнусный рахат-лукум.
Там все рассасывается до мелочей и в рот ложится, в то время как каким то зоричем или вербицким можно только жопу подтирать. Почему так, аноны? У меня ангст.
Там все рассасывается до мелочей и в рот ложится, в то время как каким то зоричем или вербицким можно только жопу подтирать. Почему так, аноны? У меня ангст.
Потому что русскоязычный бакалавриат объективнее сильнее западного, поэтому и учебники намного сложнее читать.
И много бакалавров получают неаграды по развитию математики?
Не понял посыла. Немного, есть пару гениев типа Мятисевича, Арнольда, авторов AKS алгоритма, которые в студенчестве вековые проблемы решали, но так-то немного. А что?
Почему тогда с таким мощщным бакалавриатом они пишут такие хуевые учебники?
Потому что учебники на самом деле охуенные, а ты просто неосилятор.
С такими аргументами невозможно спорить без гомерического хохота с разбрызгиванием слюней во все стороны.
Это ты должен аргументировать, почему учебники хуёвые; бремя доказательства лежит на том, кто что-то утверждает - это элементарная эристика, которую знают все образованные люди - а мы тебя будем дружно обоссывать.
Так я аргументировал уже, дорогой мой троллер.
Они говно по определению пиндосских учебников.
>Они говно по определению пиндосских учебников.
Проиграл с аргументов.
Я в другом треде все расписал. Таких как ты в универе пиздить надо, чтоб сразу привыкали и не думали, что вас че-то хорошее в жизни ждет.
Ну че ты сразу начинаешь. Пиздить - это вообще харам, ну.
Как и я с твоей аргументации.
Тебя пиздили или нет?
ты в курсе в каком году это было и какой сейчас год? говорят о сегодняшнем дне.
А какой сейчас год, еслина улице клинтон в президенты идет, все играют в покемонов и ждут новый фильм про поттериаду?!
Обобщенно пиздить же, метафизически, а не ногами.
Долбоёб не могущий в дискуссию.
Метапиздить метаногами.
Спасибо.
То чувство, когда понимаешь, что Рома Михайлов никогда не прочитает тебе лекцию про гомотопический хаос. feels.jpg
Почему не прочитает?
Калькулус томаса, по которому все студенты на западе учатся, годный или нет?
Нет, блядь, это хреновый учебник, и учатся все по нему на западе в рамках правительственной программы по оболваниванию населения.
Совершенно резонный вопрос, почему тогда его не включили в оп пост а натолкали туда говна?
Потому что у автора шапки своя призма и конечные знания.
А калькулус разве математика вообще? Я думал это какая-то хуйня для инженеров, а математики учат анализ.
>конечные знания.
Жидорептилия не палится.
Больше хуйни в тред.
Нет, ну ты мне поясняй давай, почему учебник по которому учились всякие эйнштейны не добавили в оп список?
Спроси у автора шапки. Так понятнее?
Ясно. Опять в маттреде нихуя не за математику поясняют.
Ты какой-то упоротый блять. Эйнштейны у него учились, пишешь хуйню какую-то, агришься на людей. Вообще охуеть.
так чем хорош учебник? ты смотрел сколько стоит Томас? $240. как бы я знаю, что можно украсть. когда вижу книгу за такие деньги, сразу думаю, что обман.
АНОНЫ, ТОЛЬКО ПОСМОТРИ КАКОЙ БОЛЬШОЙ ИНТЕГРАЛ Я НАШЕЛ1!!!
ОХУЕТЬ!!!
ТЫ ВИДЕЛ ТАКОЕ?!!!!
Я НЕТ!!!
УХ И ЗДОРОВЫЙ ОН!!!!!!
ОХУЕТЬ!!!
ТЫ ВИДЕЛ ТАКОЕ?!!!!
Я НЕТ!!!
УХ И ЗДОРОВЫЙ ОН!!!!!!
>Там все рассасывается до мелочей и в рот ложится
И на выходе получается энциклопедичный импотент, неспособный к мышлению. Неплохо.
Я прочитал первые пару десятков страниц в нем, увидел что он все достаточно хорошо, четко и по существу объясняет. Даже харкачер из буэ все поймет, если перевести для него.
Разве это плохой учебник?
Нет определения вещественных чисел, нет многообразий, нет фильтров, упражнения очень простые и не концептуальные (в отличии от Зорича того же). Учебник хороший, если ты в 7 классе, если ты в 10, то уже ножно что-то посерьезнее читать, хуё-моё.
>Нет определения вещественных чисел
А определение N там есть?
Такая-то универсальная паста.
Нет. Если там даже вещественных нет, то N откуда взяться?
Инштейн значит нихуя не созхдал, это через него жидорептилии слили дезу.
Так толсто что джаже тонко.
Psycholgy вообще не наука, а зашквар короче.
Математика тоже.
она из этих
formal sciences
Альзо, поцыки, что там про Мочизуку слышно? Его уже обосцалиперепроверили/опровергли?
он какую-то бамашку очередную настрочил
пока не опровергли
Пусть роботы вон опровергают, вам делать неху чтоли))
Электричество экономить надо.
Да он нас троллит. Стопудово.
Фробениусы какие-то, хуениусы.
Херня какая-то.
В жизни бреда такого не слышал.
- U wanna see some big black lazy integral? lemme show u some integral
та-тарара-тара-тара (музыка играет)
- Look at the size of his integral!
- That's why they call him black salami.
- I wish my integral was that big...
- The other day... dat guy told me to evaluate myself. And u know something? I can. Just watch.
Чего, блеать?
Я правильно понял про частные производные?
Вот возьмем формулу объема цилиндра пиr^2h
Частная производная будет равна Δh+2пиrΔr, так!?
Вот возьмем формулу объема цилиндра пиr^2h
Частная производная будет равна Δh+2пиrΔr, так!?
Нет.
А какая тогда?
А по какой переменной ты берёшь производную?
>частные производные
же.
Изменение объема при изменении высоты и радиуса основания цилиндра.
https://ru.wikipedia.org/wiki/%D0%A7%D0%B0%D1%81%D1%82%D0%BD%D0%B0%D1%8F_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D0%BD%D0%B0%D1%8F
Я надеюсь, это не ты про константу в первообразной спрашивал пару месяцев назад?
Ага, значит правильным ответом будет пиr^2Δh+2пиrΔr!?
>первообразной
Всегда бобмлио от того что неопределенный интеграл называют первобразной.
Как и от того что бесконечно малые/большие называли бесконечными а не неопределенными.
Это полная производная из частных. При взятие частной производной по одной из переменных, другие переменные ты рассматриваешь, как константы.
Я так и сделал же, ну.
Или неправильно!?
Ты частную хотел или полную?
Судя по всему я полную написал.
Но ведь она лучше частной. Тут если изменения радиуса/высоты нету уравнение упрощается до частности.
Просто частная это по одной перемнной r или h.
Ну я понял уже, все.
Надо теперь двигаться в сторону частных производных. Есть какие то книжки для этого? А то википедия мне сказала что надо дифференциальные уравнения в частных производных решать чтобы быть Ъ физеком.
Фихтенгольц.
Устарел и не нужен.
Что то поновее есть?
Зорич.
А еще варианты?
Поясните мне что тут происходит, я не понимаю почему там константа
Арнольд.
Вторая формула они логарифмируют y=x^a по рандомному основанию (э слева направо).
>a^x
>быстрофикс
Арнольд В. И. Обыкновенные дифференциальные уравнения?
Но ведь частные этьо не обычные? Или обычные?
Вот список с википедии. Сам я не в очень силён в диффурах. Можешь тут найти что-то себе.
Тихонов А. Н., Самарский А. А. Уравнения математической физики. — 7-е изд. — М.: Изд-во МГУ; Наука, 2004. — 798 с. — ISBN 5-211-04843-1.
Мизохата C. Теория уравнений с частными производными. — М.: Мир, 1977. — 504 с.
Демидов С. С. Возникновение теории дифференциальных уравнений с частными производными // Историко-математические исследования. — М.: Наука, 1975. — № 20. — С. 204-220.
Поммаре Ж. Системы уравнений с частными производными и псевдогруппы Ли. — М.: Мир, 1983. — 400 с.
>не в очень силён в диффурах.
Этому треду не хватает анонимных ученых мирового уровня.
Первообразная и интеграл соотносятся так же, как дерево и лес. Первообразная для f - любая функция, производная которой равна f. Неопределённый интеграл - множество всех первообразных.
Первообразная и неопределённый интеграл это в ТОЧНОСТИ одно и то же. Бомбит тебе видимо с собственной необразованности.
> antiderivative, primitive function, primitive integral or indefinite integral
>бобмлио от того что неопределенный интеграл называют первобразной
>ТЫ ЧО ДУРАК ШТОЛЕ???? ИТА ЖИ НИАПРИДИЛЕННЫЙ ИНТРОГАЛ НАЗЕВАЮТ ТАК
Так с чего же тебя бомбит тогда? Со слова что ли?)
Как называется хуйня типо большой буквы "П"?
Буква.
Пиздос
Мне одному кажется, что эти списки составляют люди, знакомые с "продвинутой математикой" по википедии и тифаретнику?
>КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
>Теория категорий
>Р. Голдблатт: "Топосы. Категорный анализ логики".
Зачем? Все что нужно знать про топосы (если вообще что-то нужно) есть в SGA 4.1 и в Stack Project; все топосы, появляющиеся "на практике", являются категориями пучков, для них этого более чем достаточно.
>Алгебраическая геометрия
>В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
>В. И. Арнольд: “Вещественная алгебраическая геометрия”.
И то и другое - книжки для школьников, это даже не преувеличение. Продвинутый материал, ничего не скажешь...
>Ю. И. Манин: Введение в теорию схем и квантовые группы“.
Это вообще как-то не в тему. Ну т.е. к предмету это имеет отношение, но не более того.
>R. Vakil: "Foundations of algebraic geometry".
>U. Gotz, T. "Wedhorn: Algebraic Geometry".
>E. Harris: "The Geometry of Schemes".
>Д. Мамфорд: "Красная книга о многообразиях и схемах".
Более менее нормальные учебники, вот только Мамфорд как-то устарел, даже неотделимые схемы еще предсхемами называет.
Плюс к тому ничего нет про комплексную алгебраическую геометрию, про коммутативную алгебру (а АГ без нее никуда), ничего нет про приложения (если не считать книг для школьников). Плюс совершенно любопытным образом отсутствует Хартсхорн и Qing Liu - два главных учебника по схемам помимо U. Gotz, T. Wedhorn.
>Топология
>Много ненужного для других областей математики.
Ну и зачем было про нее тогда писать?
>А. Хэтчер: "Алгебраическая топология".
Как-то совсем жиденько получилось, хоть бы у тифарета списал.
Да список ебанат полный делал, ему уже 3 или 4 анона об этом говорили.
Сделай свой, как раз на бамплимите уже.
Кстати, раз ты такой умный, скажи, какие применения у когомологий за пределами топологии? Почему на них все молятся? Я даже близко не понимаю, как они могут применяться за пределами топологических вопросов.
??!
>Кстати, раз ты такой умный, скажи, какие применения у когомологий за пределами топологии? Почему на них все молятся? Я даже близко не понимаю, как они могут применяться за пределами топологических вопросов.
Гомологии, про которые ты говоришь это почти наверняка сингулярные гомологии, те гомологии топологических пространств, что определяются во вводных курсах по топологии.
Существует целая наука - гомологическая алгебра, в которой изучаются чисто алгебраические аналоги этого объекта в т.н. абелевых категориях (есть еще обобщенное понятие "теории гомологий" в топологии - см. аксиомы Стинрода — Эйленберга ). Ее методами можно для достаточно хорошего функтора построить производный функтор, который можно рассматривать как некие "когомологии".
В частности таким образом строятся когомологии групп, алгебр Ли, когомологии пучков. Последние имеют огромное значение для алгебраической геометрии и являются частью современных оснований этой науки, этальные когомологии являются частным случаем этой конструкции.
В алгебраической геометрии также имеется понятие когомологий Вейля, т.е. когомологических инвариантов алгебраического многообразия, которые обладают достаточно хорошими свойствами. Частные случаи - сингулярные когомологии (или когомологии Бетти, для многообразий над комплексными числами), когомологии де Рама ( для полей характеристики 0), l-адические когомологии (для полей характеристики отличной от l) и кристаллические когомологии - аналог де Рама в простой характеристике. Идея о том, что эти когомологии должны быть неким образом связаны друг с другом для одного многообразия и являться по сути различными реализациями одного объекта породила идею мотива в алгебраической геометрии.
Как следует из вышесказанного, когомологии применяются повсюду в математике. В качестве базового введения в это понятие могу порекомендовать weibel introduction to homological algebra. Хорошее введение в когомологии в алгебраической геометрии содержится в Хартсхорне, да и в любом учебнике по АГ. Незаменимость этого аппарата станет очевидеой при дальнейшем изучении теории.
ЧТО ТАКОЕ ФУНКЦИЯ?
А зачем об этом спрашивать на форуме?
Это когда тебя препод по вышке на паре в жопу ебет
Давай вместе создавать.
Вот к первй части, для самых маленьких, у меня претензий нет.
Давай дальше, что ты конкретно предлагаешь?
t.великий математик
Мы говорим, что буквы языка делятся на обычные и специальные.
Мы говорим, что у специальных букв есть вес. Вес - это количество термов, которые должны быть записаны за специальной буквой (их мы называем аргументы). Терм - это, в простейшем случае, обычная буква. Аргументы мы нумеруем: первый, второй, третий и так далее.
Функция - это специальная буква, обозначим её как f, такая, что она имеет вес 2 и для любых термов, обозначенных буквами a, b, c, из fab & fac следует b=c.
Это определение функционального символа, а не функции.
Функция = функциональный символ.
А какие применения когомологий за пределами топологии и алгебраической геометрии?
Не, если великий математик тебя ебать будет это топология будет
Не так уж много областей математики находятся полностью за пределами топологии и алгебраической геометрии. Опять же, я уже сказал, что есть когомологии алгебр Ли, которые применяются в теории представлений, когомологии групп, которые применяются более менее везде. Частный случай - когомологии Галуа - лежит в основе теории полей классов в теории чисел. Это все сложные примеры - из простых, группы Ext и Tor, регулирующие классы расширений и точность тензорного произведения, встречаются повсюду в математике. В целом, с определенного момента появление когомологий в математическом тексте начинает восприниматься естественнее, чем, например, интеграла.
Я еще раз рекомендую ознакомиться с основами гомологической алгебры по хорошему учебнику - это в любом случае эффективнее, чем читать непонятные слова на анонимном форуме.
Какие есть хорошие учебники по (ко)гомологиям?
А Рамануджан знал (ко)гомологии?
Рамануджан больше угорал по дроблению чиселок по-моему, чем по каким-то абстрактным идеям и концепциям. Вот есть же там дети-аутисты, которым нравится складывать кубики, считать песчинки и всё такое. Мне кажется, у него было нечто подобное. Тоже своего рода (ко)гамалогии в том смысле, что фиг поймёшь, кому и зачем это нужно вообще, но ему вот нравилось.
Звучит больше как "я не знаю никакой другой математики, кроме топологии и алгема".
>появление когомологий в математическом тексте начинает восприниматься естественнее, чем, например, интеграла.
Больше выглядит, как какая-то искусственная надстройка, не нужная тем же группам Ли или интегралам. Я не знаю, как связана теория Галуа и когомологии Галуа, но есть ощущение, что ты подменяешь теорию Галуа когомологиями, и на этом основании пытаешься увеличить их значимость.
>Я еще раз рекомендую ознакомиться с основами гомологической алгебры по хорошему учебнику
Ну и понятно, что можно посвятить всю жизнь чтению хороших учебников, вот только пока не понятен даже смысл.
Ну т.е. вокруг нас двсы, компы на полупроводниках, гпсы - понятные осязаемые вещи, из них непосредственно возникает мотивация ботать физику. Не теорию струн, конечно, а нормальную физику. Аналогично вокруг поисковики, системы управления ядерными реакторами, логистика, есть мотивация ботать теорверы, дифуры с тау, теорию графов.
А в чем смысл ботать когомологии, если на вопрос "а нахуйа оно вообще" отвечают "просто читай учебник, не задавай вопросов"
Твоё определение не согласуется с общепринятым.
С моей т.з. только один - который я уже рекомендовал (Weibel). В нем больше материала, чем в любых других, и он современнее. Но объективно он довольно сложный, поэтому многие до сих пор читают Маклейна или Картана Эйленберга. В принципе есть еще Ротман, но мне он сильно не понравился затянутостью и обилием элементарных упражнений. Есть еще Гельфанд Манин "Методы гомологической алгебры" том 1 (том 2 никогда не вышел). В нем больший упор на симплициальные методы, производные и триангулированные категории и т.п. умные вещи. Они весьма в принципе весьма полезны, о большим его недостатком является практически полное отсутствие базового материала, так что я не назвал бы его учебниеом, хотя книга сама по себе забавная.
> Звучит больше как "я не знаю никакой другой математики, кроме X".
> А в чем смысл ботать X, если на вопрос "а нахуйа оно вообще" отвечают "просто читай учебник, не задавай вопросов"
Welcome to pure mathematics
>Ну т.е. вокруг нас двсы, компы на полупроводниках, гпсы - понятные осязаемые вещи, из них непосредственно возникает мотивация ботать физику. Не теорию струн, конечно, а нормальную физику. Аналогично вокруг поисковики, системы управления ядерными реакторами, логистика, есть мотивация ботать теорверы, дифуры с тау, теорию графов.
Это всё математика первого курса. Для изучения математики второго курса нужны другие мотивации.
Слово "чистая" имеет какие-то слишком положительные коннотации.
Правильнее было бы "искусственная", "бессмысленная", "ненужная".
Крайне наивная технарьская точка зрения. Ты, наверное, еще и атеист?
А мы что, задели религиозную тему? Похоже на то.
В таком случае какая польза от твоих молебнов уродливым идолам из категорий и топосов стране и почему она должна платить тебе зарплату? У нас светское гос-во, кто хочет, молет кому и чему захочет у себя дома. Но какое отношение это имеет у математике, университетам и по какому праву вы свой опиум для народа толкаете на матфаках детям?
Для государства - очевидно. На уровне государства, количество выдающихся учёных - фаллометрическая игра повышающая престиж на мировой арене. Ровно как и количество вооружения и спортивные достижения. Даже странно, что такие простые вещи приходится объяснять.
> по какому праву вы свой опиум для народа толкаете на матфаках детям?
Что значит "по какому праву"? Нет никакого "права". Есть просто группы людей, которые приследуют свои интересы. Каждая группа "толкает" детям свои ценности. Ты вот навязываешь свой технофашизм и совковый образ мышления.
>А мы что, задели религиозную тему? Похоже на то.
Просто это местный шизик-этотерик, которой утверждал, что каждый математик должен быть мистиком. Проходи мимо него, пусть обмазывается своим категорным говном без задач.
Они не уродливые, а вполне няшные. Никто никому ничего не должен на самом деле. Ни за топосы, ни за интегральчики.
> праву вы свой опиум для народа толкаете на матфаках детям?
Я был бы не прочь, если бы мне толкнули, но всё приходится самому.
Просто есть вещи, интересные людям. А государство и прочее там общество идут лесом. Если государство не прочь выебнуться хиршами/учёными щкалами, подкормить грантами - ну так это не маняматическая проблема, а государства. Зачем из-за этого ругать гамалогии? Они ни в чём не виноваты.
Так вся наука имеет глубоко эзотерическую структуру.
Пруф.
А разве это не чувствуется? Любой завершённый рассказ, будь-то о Вселенной или о жизни, начинается с некоторого мифа - большой взрыв, первичный бульон. Постоянно возникают новые трактовки, а старые "увядают", постоянно идёт процесс сотрясания основ и перестройки всего унивёрсума (Ньютон -> Эйнштейн -> Виттен(?) ), это очень типичное поведение для эзотерических и философских учений европейского типа; отсутствие "начала" в логической структуре - сколько бы не говорили о большом взрыве или чём-то таком, всегда можно "двинуться дальше" и рассказывать всё более и более фантастические (здесь это слово сказано без всяких отрицательных коннотаций) истории.
То есть я должен поверить тебе только из-за того, что ты что-то там почувствовал? А если какой-нибудь гуманитарий почувствует, что математика говно и не нужна, то он будет прав?
из того, что элементы рядов a_n ≤ b_n и ряд с элементами b_n сходится, следует, что ряд с a_n сходится.
ошибка в книге или почему в примере рядов:
1/(n(n + 1)) < 1/n^2 < 1/(n(n - 1))
доказываем сходимость 1/n^2 по 1/(n(n + 1)), а не по 1/(n(n - 1))? см. картинку.
ошибка в книге или почему в примере рядов:
1/(n(n + 1)) < 1/n^2 < 1/(n(n - 1))
доказываем сходимость 1/n^2 по 1/(n(n + 1)), а не по 1/(n(n - 1))? см. картинку.
Посоветуйте книгу/сайт, где были бы хотя 100 примеров линейных операторов в разных векторных пространствах и возможно рассматривались их свойства. Абстрактные теоремы не нужны. Ересь теории категорий не нужна. Нужно как можно больше вычислительных примеров. Приложения желательны, но не обязательны. Может быть это будет книга по экономике или еще чему-то такому. Или задачник по численному анализу. Хрен знает где такое бывает.
Задачник Проскуряева.
> я ничего не знаю но по моиму фигня какаято!
Ты из тех людей, которые triggered на слово "чувствуется"? Хорошо, хоть никакой аллюзии на религию не привёл.
Окей, а что в твоём понимании должно быть пруфом в этом случае? Лингвистический анализ структур эзотерических и научных текстов? Или ссылка на авторитетного социолога/текстолога, который говорит "да, хуё моё, что-то в этом есть, бля"?
>А если какой-нибудь гуманитарий почувствует, что математика говно и не нужна, то он будет прав?
Нормальный гуманитарий, в отличии от тебя, знает, что категории "нужна/не нужна" оценочные и имеют смысл только в рамках некоторой системы ценностей / языковой игры.
- >
Тебя нельзя заниматься математикой. Иди в /mg!
>Ты из тех людей, которые triggered на слово "чувствуется"? Хорошо, хоть никакой аллюзии на религию не привёл.
Чувства не доказательства и не могут ими быть.
Чувства не доказательства и не могут ими быть.
Глупости. Эти фантазии со временем подтверждаются экспериментально, а в те фантазии, которые еще не подтверждены, люди верят в том случае, если видны какие-то веские причины, по которым они могут быть верны. Эксперимент характерен тем, что его можно повторить, это не какое-то чудо, которое якобы кто-то когда-то видел и записал в эзотерическую книгу. Конечно, эксперимент может быть ошибочным и выводы могут быть неправильными, но отличия от эзотерики очевидны. В математике для верификации есть доказательства. Они могут содержать ошибки, но все-таки доказательства это не просто какие-то маняфантазии.
Когда я спрашивал того анона, не атеист ли он, я имел в виду, что думать, что мир можно описать какой-то формальной системой, и все люди, у которых есть соответствующие способности, должны работать над этой системой - это полная глупость. Я не утверждал, что математик должен жрать грибы и думать, что он превращается в животных (хотя, ничего плохого в этом не вижу).
Ряд 1/n(n - 1), n от 2 - это все равно что ряд 1/n(n+1), n от 1.
Это очень наивная точка зрения.
Экспериментально можно подтвердить предсказательную силу какого-то форализма, а не его интерпретацию. К тому же в физике нередки ситуации, когда формализм даёт хорошую предсказательную силу в одних ситуациях и совершенно плох в других. Грубо говоря, в первом классе мы все хуярили все задачи - про количество воды в бассейне, книг на полочке и птичек на дереве линейным уравнением. Но это совершенно не значит, что полное понимания "теории линейного уравнения" приведёт к пониманию того, что такое книги на полочке и птички на дереве.
>это не какое-то чудо, которое якобы кто-то когда-то видел и записал в эзотерическую книгу.
Но вот большой взрыв и образование первичного бульона нельзя повторить - это миф, удобная метафора, служащая воспомогательной для освоения какой-то формальной знаковой системы, которая может прекрасно согласовываться с определённой группой экспериментов, что, как по мне - не "подтверждает" первичный бульон или большой взрыв в каком-то онтологическом качестве.
> Конечно, эксперимент может быть ошибочным и выводы могут быть неправильными, но отличия от эзотерики очевидны.
Я не говорю, что их нет, я только говорю, что не нужно отрицать очевидные сходства.
> В математике для верификации есть доказательства. Они могут содержать ошибки, но все-таки доказательства это не просто какие-то маняфантазии.
Это могут быть "маняфантазиями" в рамках одних научных школ и доказательствами в рамках других. Например, алгебраисты не принимают proof by pictures - ты ни найдёшь ни одного уважающего себя алгебраического научного журнала, в котором такое бы было, а топологи вот принимают. При этом даже не вполне очевидно, что их принципиально можно формализовать до уровня исчисления предикатов. Но живут же как-то.
Согласуется. Я ведь не отображение определяю.
В большинстве учебников это одно и то же.
В большинстве учебников не начинают изложение с языка предикатов, но это не делает ZFC несуществующей. А в аксиомах ZFC термин "функция" нужен при формулировании аксиомы преобразования.
В большинстве учебников по логике различают ункциональный символ и функцию.
Пруф: Клини, Cori Lascar, Манин.
Проиграл с этого бурбакиста.
Учебники Клини малоизвестны. У Манина вообще не учебник, а так, подшивка лекций. В оригинальных работах основателей, например у Цермело и Хаусдорфа, функция понимается именно как функциональный символ (например, в определении упорядоченной пары).
Оригинальные работы основателей вторичны при обсуждении актуальности той или иной терминологии. Неужто неочевидно?
>Учебники Клини малоизвестны.
Лол.
Это тебе нельзя. Математик, который не умеет работать на мистическом уровне, а умеет только на техническом и на фактическом - не математик.
Я не согласен с этим.
Именно так, судя по вузовским библиотекам.
>Я не согласен с этим.
Ну дурак ты тогда, чего ещё сказать можно.
Фи.
Функция — это гомоморфизм в категории множеств.
Функция — это функтор в дискретной категории.
Функция — это терм функционального типа.
Функция — это упорядоченная тройка из множества упорядоченных пар, множества определения и множества значений.
Продолжение банкета
Аноны, спасибо за все что собрано в шапке! Спасибо! Я вас обожаю
Аноны, спасибо за все что собрано в шапке! Спасибо! Я вас обожаю
Там куча неструктурированного говна. Не за что!
Не за что, старались высрать туда говна как можно больше.













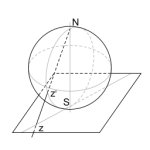







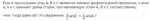












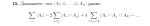















Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Геометрия
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
Начала анализа
Б. М. Давидович: “Математический анализ в 57 школе“.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec