сажаскрыл
ОП, а почему теории Монтидзуки тред не посвятил? Это же самая актуальная и насущная проблема современной математики. Поразбирались бы всем тредом. Как-то шкурнически поступил.
Натуральные числа в хату посоны. Тому кто не даст нормального определения нож под ребро да хуй в рыло.
> Этот тред будет посвящен алгебраической K-теории
Когда будет тред посвященный определению N?
я сделяль
Предлагаю тред посвятить обсосу и пропердоливанию математического лайфхака из прошлого треда, что-то из области фокусов
Мне он показался прикольным и доступным для пониманию любому, проходившему матан.
Я своё ыкспердное заключение + дал - кто даст больше?
Еще поясните за , если поконкретнее то
>Еще ассоциация в связи с этим вопросом - сумма ряда ассоциативна но не коммутативна(перестановкой слагаемых сходящегося ряда можно добиться любой суммы на выхлопе), сей факт я не смог осознать до сих пор по-видимому.
Также был проигнорен мой пост(в связи с перекатом)
Простите за вниманиеблядство, если чё.
ЗЫ. Как же меня бесит новая быдлокапча
Мне он показался прикольным и доступным для пониманию любому, проходившему матан.
Я своё ыкспердное заключение + дал - кто даст больше?
Еще поясните за , если поконкретнее то
>Еще ассоциация в связи с этим вопросом - сумма ряда ассоциативна но не коммутативна(перестановкой слагаемых сходящегося ряда можно добиться любой суммы на выхлопе), сей факт я не смог осознать до сих пор по-видимому.
Также был проигнорен мой пост(в связи с перекатом)
Простите за вниманиеблядство, если чё.
ЗЫ. Как же меня бесит новая быдлокапча
Спасибо.
Давайте вьебем по рамануджанчику для затравки. Либо просто попиздим о ходе обоснования
http://репетитор-по-математике.рф/penemumop-no-MATEMATuKE/3.html
Я думаю там используется рекуррентное соотношение, по которому берется предел и решается уравнение - это еще смутно из учебника матана всплывает. Откуда там 5 страниц - в душе не ебу, может я недостаточно строго всё представил.
Какие ваши предложения?
http://репетитор-по-математике.рф/penemumop-no-MATEMATuKE/3.html
Я думаю там используется рекуррентное соотношение, по которому берется предел и решается уравнение - это еще смутно из учебника матана всплывает. Откуда там 5 страниц - в душе не ебу, может я недостаточно строго всё представил.
Какие ваши предложения?
С выселением N-петухов, первое время тут будет тухло.
Кто-нибудь хочет порешать Topology - J. Munkres? Солюшн мануала вроде как нет, поэтому хочется с кем-то скооперироваться и показывать друг другу доказательства.
сорян, я шизопрограммист мамкин - топологию мы не проходили, хотя в принципе мне это интересно, но лень. Дефолтные инженерные матдисциплины(матан, линал, дифуры, дискретка) я себе хотя бы как-то представляю. Так-то я хотел как-то самостоятельно изучить основы тензоров - но в итоге прокрастинировал пока не положил хуй.
Я, но не прямо сейчас, где-то осенью начну её читать.
Анон, поясни за
http://homepages.math.uic.edu/~acamer4/math300/aluffi.pdf
учебник по алгебре. Хороший, годный? Какие варианты еще есть, чтобы можно было читать без бэкграунда?
http://homepages.math.uic.edu/~acamer4/math300/aluffi.pdf
учебник по алгебре. Хороший, годный? Какие варианты еще есть, чтобы можно было читать без бэкграунда?
Хороший, годный, современный. Из вариантов Ван дер Варден и Лэнг, но им уже много лет.
Мишин учебник уже прорешал?
Не, чет не хочется. Во-первых, он там в предисловии написал, что в его учебнике много опечаток, во-вторых, судя по твиттеру, он ебнутый, поэтому я ему не доверяю.
Твиттер ведёт какой-то посторонний хуй, Вербит ведёт только жежешку.
И после вот такого http://lenta.ru/articles/2012/04/13/boroda/ он имеет полное право беспощадно ненавидеть Россию.
Ну и дурак, раз такие причины.
По-моему - это эпохальный конец маттредов
Халп. Есть задача - найти как можно больше предельных циклов в динамической системе. Подскажите возможный алгоритм для их поиска. На вход будет даваться система, например уравнение Ван дер Поля (1 предельный цикл) или системы с полиномом справа (несколько циклов), какие необходимо сделать проверки/операции перед использованием метода Рунге-Кутта? И как найти неустойчивые циклы в данной системе?
Здравствуй, петушочек. Как жизнь?
Завтра запилю тред в д с жалобой на дегенерата-аватаркофага.
Где ты видишь аватаркофага?
Вы только посмотрите, что ваш кумир пишет. Это же чистый экстремизм!
https://twitter.com/misha_verbitsky/status/639676540939304960
https://twitter.com/misha_verbitsky/status/639676540939304960
>Твиттер ведёт какой-то посторонний хуй, Вербит ведёт только жежешку.
Религию он запретить хочет, вот же уебок. А математика это как будто не религия. Кризис основ математики, а также торема Геделя ясно показывают, что нихуя в математике не определено, что все на чем строится математика - противоречиво. Это такая же религия, разве что бабахов в ней нет.
Среди посетителей тифаретника это теперь такой мемчик притворяться что твитер вербита пишет вербит?
Сказано-сделано. Будем ждём ответа. Sci - не место для анимедебилов-аватаркофагов. Первые треды начинались с портретов великих. А теперь какой ублюдок использует их для постинга своей блевотной нерелейтед хуеты.
Ответил.
Основы в математике может кризятся и противоречатся, только математика работает(в том числе на реал-лайф моделях через физику) и развивается, а религия - нет. Если не брать в расчёт бабахи и резню ИГИЛа.
Ну посмотри в тифаретнике такой же пост
Но это офтоп
Что такое когомология, почоны?
Математики, кому не лень, объясните унтерменшу как можно проще и доступнее, что это за такие пространства. Вкратце о каждом: что из себя представляет, где применяется, какие-то может отличительные особенности, которые могут быть интересны для общего развития, человеку далекому от математики. А то увидел красивую картинку, а что это такое не представляю себе даже примерно.
отклеилась
Только, если можно прям как для самых маленьких. Как будто 11-класснику.
>что это за такие пространства
Множества, с определенными аксиомами, и операциями, которые на них определены. Например, линейным пространством называется непустое множество X, с элементами произвольной природы, для которых определены 2 операции: сложение и умножение на число, так, что оказываются выполненными 8 аксиом для этого пространства. Поле (множество) действительных чисел тоже может быть рассмотрено как евклидово пространство (т.е такое, на котором определена операция скалярного умножения). В общем случае пространство - это абстракция, и нарисовать мы его не сможем ( и представить, в общем то тоже. ). Как пример - бесконечномерные Гильбертовы пространства. Применений дохуя - от всяких задач вариационного исчисления, до квантовых компьютеров, и.т.д и.т.п
> что это за такие пространства
Это множества с определенными свойствами.
Я сам погуглил чуть-чуть. Но мне никогда нигде не объясняли про множества. Я наверное совсем тупенький, но я не смог найти как перевести на русский предпоследнее с картинки. Про последнее в какой-то научно-популярной статье читал, что-то вроде- одно из основных свойств "АВ не равно ВА"- для гсм норм объяснение, или наглый пиздеж?
>но я не смог найти как перевести на русский предпоследнее с картинки
Measure space - пространство с мерой. На рисунке изображено канторово множество.
> что-то вроде- одно из основных свойств "АВ не равно ВА"- для гсм норм объяснение, или наглый пиздеж?
Да. Операция умножения не является коммутативной, но там всё намного сложнее.
Я прекрасно понимаю, что в действительности мой уровень знаний ОЧЕНЬ далек от необходимого, чтобы все это понять. Я и прошу простейших объяснений. На уровне "вот в этом случае АВ не равно ВА из этого следуют такие-то приколные штуки(второе-опционально)" Почему-то особенно интересует как раз последнее, но про остальные тоже любопытно узнать
Ну, вот смотри. У нас есть вещественные числа. Для того чтобы некоторое множество было линейным векторным пространством, необходимо выполнение 8 аксиом.
1) x+y = y+x для любых x,y из этого пространства. Пример: 4+12=12+4
2) (x+y)+z=x+(y+z). Пример: (5+2)+7=5+(2+7)
3) В множестве существует нулевой элемент 0_L такой, что x+0_L = x. Пример: 11 + 0 = 11
4) Для любого элемента множество существует противоположный элемент (-x) в том же множестве, такой, что x+(-x) = 0_L. Пример: 18+(-18) = 0_L
5) 1x = x для любого x.
6) A(Bx) = (AB)x
7) (A+B)x = Ax+Bx
8) A(x+y) = Ax+A*y
Это верное и для векторов, и для матриц, и.т.д.
Теперь о (не)коммутативности умножения как пример:
Возьмем кольцо всех матриц (множество) размерности n на n.
Возьмем две матрицы {{1,1},{0,1}} и {{0,1},{0,1}}. Если будем умножать первую на вторую - то выйдет {{0,2},{0,1}}, если наоборот - {{0,1},{0,1}}, т.е умножение матриц - не коммутативно AB != BA.
С первой частью все понятно, спасибо. Со второй хуже. "кольцо всех матриц"- это по ходу для подростков, а я еще маленький. Как именно производится умножение матриц посмотрю на досуге, думаю, что смогу понять. Когда мы определяем это пространство(можно так сказать?) фишка с некоммутативностью единственная, которой отличает его от того же векторного? Это же банально выкинутая на мороз шестая аксиома, я правильно понял?
Т.е. я могу запилить любой набор аксиом, лишь бы они не противоречили друг другу и это буде мое пространство с блекждеком... ? ...если только кто-то не запилил его раньше
Т.е. я могу запилить любой набор аксиом, лишь бы они не противоречили друг другу и это буде мое пространство с блекждеком... ? ...если только кто-то не запилил его раньше
Допустим, есть несколько теорем. Для того, чтобы они были верны для какого-то множества, нужно, чтобы это множество обладало определенными свойствами и с элементами этого множества можно было делать определенные операции. Эти свойства и операции мы можем выделить и как-то обозвать все подобные множества.
Пример. Если для любых двух элементов множества мы можем вычислить расстояние между ними и выполняется еще несколько свойств, которые тебе неинтересны, такое множество называется метрическим пространством. Например, обычное трехмерное пространство R3, будет метрическим, если мы правильно определим функцию, вычисляющую расстояние между точками. Есть больше 1 способа определить эту функцию так, чтобы выполнялись всякие интересные свойства. Именно поэтому мы не говорим, что метрика - это функция distance(p, q) = sqrt((xq - xp)^2 + (yq - yp)^2 + (zq - zp)^2), а говорим, что это функция, обладающая такими-то и такими-то свойствами.
ой, не 6-ая, ну ты понял
Я могу запилить свое пространство и сказать, что... ну, например... существуют элементы расстояние между которыми и любым другим элементом отрицательное? (просто, что первое в голову пришло)
Метрика всегда положительна. Так как 0 = p(x,x) <= p(x,y) + p(y,x) = 2*p(x,y)
Можно на пальцах объяснить что такое метрика? А то я не совсем уверен, что правильно понимаю этот термин. На этом закончу доебываться и уйду.
Ты можешь открыть здесь https://ru.wikipedia.org/wiki/Метрическое_пространство раздел "примеры" и проверить, что для метрик, которые там приведены, выполняются свойства, которые написаны в определении. Можешь и свою метрику придумать.
ТОЧНО последний вопрос. Из аксиом выше, есть ли такие, которые актуальны вообще ДЛЯ ВСЕХ пространств?
Расстояние между элементами пространства. Для вещественных чисел метрика будет p(x,y) = |y-x|
Это функция, удовлетворяющая свойствам, которые написаны в определении.
Нет. Пространства Соболева или L_p как пример.
Нет, в метрическом пространстве нет операций сложения и умножения элементов. Однако, ничто не мешает множеству одновременно являться линейным и метрическим пространством, если ты придумаешь метрику и способ складывать и умножать элементы этого множества. Самый простой пример
> Для вещественных чисел метрика будет p(x,y) = |y-x|
а складывать и умножать можешь как обычно. Тогда множество вещественных чисел с операциями умножения и сложения будет линейным пространством, а с описанной выше функцией p - метрическим.
Спасибо благородным донам за просветительскую деятельность. Если вдруг кто-то знает, где можно прочитать хоть что-то про некоммутативное пространство на научно-популярном уровне, а не на "языке формул", то буду премного благодарен.
Думаю, что нигде. Да и зачем тебе оно нужно, если ты не математик(околоматематик)?
Любопытство, ничего более. В школе математику любил. Уровень неплохой, но не профильной математической школы. Но корка юриста гарантировала мне сытую жизнь, поэтому теперь мозг малость атрофировался.
Ооо... раз тут такое дело, то еще один любознательный гсм-нутый врывается в тред. Есть ли разделы математики, которые появились совсем недавно? Или же изучают все те же яйца, что были известны еще дедам, только теперь в профиль? Если есть- киньте пару-тройку названий того, что как можно новее.
>Есть ли разделы математики, которые появились совсем недавно
Arithmetic deformation theory
Derived algebraic geometry
ну и прочая Мочидзука там с её Inter-Universal Teichmuller Theory
Ради того, чтобы называться Мочидзукистом я готов бросить все и начать познавать математику с нуля, лишь бы настал тот час, когда моих знаний оказалось бы достаточно, чтобы понять Мочидзуку и всю ее силу и мощь
Я, пожалуй, начну с того, что восстановлю в памяти материал школьного курса. Вроде как в школе любимым предметом была геометрия.
Мочидзуку-то не осилишь, один хуй
никто не осилит
Ну чё, Фесенко осилил же.
Эта ваша некоммутативная геометрия изучается студентами где-то кроме мехмата и аналогичных факультетов других шараг? Мочидзука вообще где-то изучается?(путь даже и как опциональные дисциплины)
>Мочидзука вообще где-то изучается?
Совсем нигде. Но возможно Мочикудза дает лекции в RIMS
http://www.kurims.kyoto-u.ac.jp/en/index.html
>некоммутативная геометрия изучается студентами где-то кроме мехмата и аналогичных факультетов других шараг?
Наверное только на кафедре дифференциальной геометрии и приложений МГУ, и то вряд ли.
Будущий Мочидзукист возвращается в тред. За чашкой чая решил спросить у гугла ху из миситер Мочидзука. Дошел до статьи в википедии abc-гипотеза. Со временем подтяну свои знания, чтобы понять о чем она. Но почему-то есть подозрение, что это что-то такое, что можно в общих чертах объяснить такому как я на пальцах, или нет?
Для любого действительного числа r > 1 существует не более конечного числа троек натуральных чисел a, b, c таких, что для них выполнены одновременно три условия:
1)a + b = c
2)a, b и c взаимно просты в совокупности (то есть у них нет общих делителей)
3)c > rad (abc)^r
Радикалом rad натурального числа N называется число, которое представляет собой произведение всех различных простых (простым называется отличное от единицы число, которое делится только на себя и на единицу) делителей числа N. Например, rad(15) = 15 потому, что у этого числа простые делители 3 и 5, а rad(18) = 6, так как простых делителей у числа 18 ровно два — это 3 и 2.
Ну и великая теорема Ферма, наряду с еще 13 проблемами, кажется, является частным случаем этой теоремы. (Которые автоматически будут считаться решенными, в случае доказательства abc-гипотезы)
>Но почему-то есть подозрение, что это что-то такое, что можно в общих чертах объяснить такому как я на пальцах, или нет?
Абсолютное большинство недоказанных гипотез из теории чисел, формулируются на уровне, доступном пятикласснику, но только доказательство таких теорем - совершенно нетривиальное. Подумай на досуге, почему так.
Матаны, пиздец. Опоздал на 30 минут на свою первую в жизни лекцию по матану, так еще и не понял больше половины того, что было сказано потом. Еще и препод не супер для ньюфага, как-то быстро объяснял + приводил дурацкие примеры про мячи. Спросили насчет литературы - сказал, что нормальных учебников нет, но таки написал фамилии Фихтенгольца, Кудрявцева и Зорича, при этом утверждая, что лучше все сразу не читать и вообще начните с чего-нибудь попроще. Может быть хоть анон поможет мне. Что читать кароч?
Читай Фихтенгольца Если дебил. Зорич для математиков больше подойдет Можешь читать его, если не дебил.. Кудрявцев - хрень как по мне.
>Но мне никогда нигде не объясняли про множества.
Прочитай книжку "Рассказы о множествах", написал Виленкин. Там и про пространства есть.
Просто пока ты не разобрался в том, что из себя представляют множества, бессмысленно объяснять тебе, что такое операции на множестве - вовсе не потому что ты глупый, просто вместо объяснения получится размахивание руками.
Если не ориентируешься в теории множеств, то тоже советую Виленкина. Книжка Зорича - лучший учебник матана на русском языке для начинающих. Не потому что эта книжка очень хорошая; она объективно плохая, обозначения в ней громоздкие, а изложение слабо логичное. Вторая половина первого тома (начиная с кеплеровой задачи) вообще треш. Просто все остальные учебники ещё хуже.
Спасибо. Найду, прочитаю. На данный момент я себе представляю множество как набор элементов(пофигу каких именно) лишь бы они все подчинялись каким-то общим для всех этих элементов правилам
Я смотрю, теперь этот тред захвачен любопытными нубами, внесу свои 5 копеек. Есть такое заведение ИППИ РАН, так вот оно очень гордится тем, что среди его сотрудников 3 Филдсовских лауреата. Как бы понятно, что исходя их специализации института, математики ему нужны... но правильно ли я понимаю: этому заведению интересны математики, специализирующиеся на каком-то ДОВОЛЬНО УЗКОМ наборе дисциплин, актуальных для его тематики? И если ты занимаешься какой-то другой областью, то ты этому заведению не интересен?
Маргулис специалист в области эргодической теории, Концевич работает во Франции и связан со струнной теорией, Окуньков - занимается теорией представлений ( опять же работает в США вроде). Сам институт занимается какой-то хуитой в области геномики.
Вот вы тут говорите, что 21 век на дворе, вся вычислительная хренотень должна делаться нормальными людьми в матпакетах на комплюхтере, а не на бумаге. Как мне узнать разрешимость группы Галуа многочлена? В каких продуктах это реализовано и как юзать?
Собственно, вопрос на пике.
Почему определение непрерывности выглядит не вот так?
Почему определение непрерывности выглядит не вот так?
Анон, среднеквадратичная сходимость функций (сходимость в C_2[a,b] влечёт равномерную сходимость или наоборот?
Господа, а тут есть кто-нибудь, кто угорает по теории чисел?
Меня, например, приятно удивила явная формула(пикрилейтед) для счастливого билета - или это уже комбинаторика? Как вообще из такой хуйни могут появиться подобные интегралы?
Также вопрос олдфагам мат. тредов - вы студенты/выпускники мат. факультетов или хуи простые, как я лол? Я в своё время мог на прикладную математику поступить(потом раздумывал переводиться на неё), но пошёл на погромиста - о чём не жалею, т.к. математику в качестве хобби можно самому изучать/решать задачи, а погромирование как способ заработка мне представляется более предпочтительным - тем более оно тоже интересно и переплетается с математикой.
Меня, например, приятно удивила явная формула(пикрилейтед) для счастливого билета - или это уже комбинаторика? Как вообще из такой хуйни могут появиться подобные интегралы?
Также вопрос олдфагам мат. тредов - вы студенты/выпускники мат. факультетов или хуи простые, как я лол? Я в своё время мог на прикладную математику поступить(потом раздумывал переводиться на неё), но пошёл на погромиста - о чём не жалею, т.к. математику в качестве хобби можно самому изучать/решать задачи, а погромирование как способ заработка мне представляется более предпочтительным - тем более оно тоже интересно и переплетается с математикой.
Вангую тебя щас хуями обложат за эпсилон-дельта.
Мой ответ - в определении непрерывности из условия на аргумент должно следовать условие на функцию(т.к. определение можно записать через пределы), возьми определение предела по Гейне для сравнения. Мы же "стремимся" к x0 по аргументу и смотрим на значения функции а не наоборот. Это как с пределом последовательности - мы стремимся к бесконечности по N(это как бы аргумент функции, задающей последовательность), а не по значению a_n.
GAP вроде умеет.
http://www.gap-system.org/
Это комбинаторика.
http://ega-math.narod.ru/Quant/Tickets.htm
>среднеквадратичная сходимость функций (сходимость в C_2[a,b] влечёт равномерную сходимость
Да.
Советую Magma Online Calculator.
В Maple ещё функция есть, там совсем просто, но там поддерживаются многочлены только до 9 степени.
>Подумай на досуге, почему так.
Правильный ответ: потому что тч говно, да ещё и без задач к тому же?
Может оно и без задач - зато может играть роль полигона для применения теории из других разделов и интеллектуальной игры для мозгоёбов-извращенцев.
ОП, поясни за (алгебраическую) К-теорию - чё от неё все прутся так? Для чего она нужна ваще? Просто какую книгу ни открою - везде, блин, надо знать алгебраическую геометрию на уровне харстхорна, а это ойтакещёнескоро. Можешь на пальцах рассказать, чо да как, в чём там ништяк?
Все Sage в этом треде!
http://www.sagemath.org/
http://www.sagemath.org/
А может всё-таки равномерная влечёт среднеквадратичную?
По ссылке же подробнейшим образом написано, что это такое и где это нужно.
Есть штуки, которые называются топологические многообразия. Это известные тебе геометрические фигуры - шар, тор, лента Мёбиуса, поверхность Земли и так далее.
Берём какое-то топологическое многообразие и каждой его точке сопоставляем векторное пространство так, чтобы локальная топологическая структура многообразия наследовалась в векторном пространстве. Простейший пример - с каждой точкой нашей планеты связываем локальную плоскую карту, т.е. двумерное векторное пространство. Локальная карта произвольного многообразия может быть и двумерной, и трёхмерной, и вообще многомерной, конечно. Топологическая структура наследуется - значит, точки, близкие на многообразии, близки и в векторном пространстве. В этом случае говорим, что многообразие расслаивается на векторные пространства. Набор данных многообразие+векторные пространства в каждой точке называем тогда векторным расслоением.
Далее рассматриваем все возможные векторные расслоения на многообразии, то есть все возможные покрытия многообразия картами. Оказывается, они формируют категорию. Объекты в ней - это векторные расслоения (т.е. разбиение многообразия на карты), а стрелки - это, грубо говоря, функции, представляющие карты одного расслоения в картах другого расслоения.
Некоторые векторные расслоения оказываются изоморфными, то есть бывают, в некотором смысле, эквивалентные покрытия многообразия картами. Мы тогда проводим факторизацию. Каждому классу эквивалентности расслоений мы сопоставляем один и только один объект, называемый попросту "класс". Множество всех классов расслоений многообразия X обозначается тогда просто K0[X].
У многообразий могут быть свойства - например, эйлерова характеристика. Эйлерова характеристика управляет формой многообразия. Например, эйлерова характеристика сферы равняется двум, поэтому если правильный футбольный мяч сшит из пятиугольников, то их должно быть двенадцать. Эйлерова характеристика, и вообще топологические характеристики, чрезвычайно полезны для изучения этих ваших графенов, фуллеренов и так далее. Впрочем, химики пока что редко это используют.
Некоторые свойства многообразий могут быть эквивалентными. Например, возможны два совершенно не похожие друг на друга многообразия, которые обладают одной и той же эйлеровой характеристикой. Это полезно, потому что вместо изучения сложных многообразий можно изучать простые. Однако очень трудно выяснить, какие свойства являются у двух произвольных многообразий общими. Оказывается, что если есть два многообразия, X и Y, то если построить их классы K0[X] и K0[Y] и специальным образом отобразить их друг в друга, то можно будет довольно простой проверкой, чуть ли не тупыми вычислениями, находить у многообразий общие свойства.
Это специальное отображение между K0-классами многообразий называется функтором K0. Кроме K0, существуют ещё функторы K1, K2 и даже Kn, чем больше n, тем навороченнее. Изучение функторов K называется K-теорией. Грубо говоря, K-теория - это изучение соотношений между разбиениями многообразий на карты.
Алгебраическая K-теория изучает функторы K, используя их чисто алгебраические свойства. Например, K0[X] является абелевой группой, что даёт возможность использовать теоретико-групповые инструменты. Ещё есть топологическая K-теория, использующая методы из общей топологии.
В частности, с помощью K-теории можно выяснить, насколько форма вселенной напоминает жопу твоей мамаши, путём изучения отношений между картами вселенной и картами жопы.
Есть штуки, которые называются топологические многообразия. Это известные тебе геометрические фигуры - шар, тор, лента Мёбиуса, поверхность Земли и так далее.
Берём какое-то топологическое многообразие и каждой его точке сопоставляем векторное пространство так, чтобы локальная топологическая структура многообразия наследовалась в векторном пространстве. Простейший пример - с каждой точкой нашей планеты связываем локальную плоскую карту, т.е. двумерное векторное пространство. Локальная карта произвольного многообразия может быть и двумерной, и трёхмерной, и вообще многомерной, конечно. Топологическая структура наследуется - значит, точки, близкие на многообразии, близки и в векторном пространстве. В этом случае говорим, что многообразие расслаивается на векторные пространства. Набор данных многообразие+векторные пространства в каждой точке называем тогда векторным расслоением.
Далее рассматриваем все возможные векторные расслоения на многообразии, то есть все возможные покрытия многообразия картами. Оказывается, они формируют категорию. Объекты в ней - это векторные расслоения (т.е. разбиение многообразия на карты), а стрелки - это, грубо говоря, функции, представляющие карты одного расслоения в картах другого расслоения.
Некоторые векторные расслоения оказываются изоморфными, то есть бывают, в некотором смысле, эквивалентные покрытия многообразия картами. Мы тогда проводим факторизацию. Каждому классу эквивалентности расслоений мы сопоставляем один и только один объект, называемый попросту "класс". Множество всех классов расслоений многообразия X обозначается тогда просто K0[X].
У многообразий могут быть свойства - например, эйлерова характеристика. Эйлерова характеристика управляет формой многообразия. Например, эйлерова характеристика сферы равняется двум, поэтому если правильный футбольный мяч сшит из пятиугольников, то их должно быть двенадцать. Эйлерова характеристика, и вообще топологические характеристики, чрезвычайно полезны для изучения этих ваших графенов, фуллеренов и так далее. Впрочем, химики пока что редко это используют.
Некоторые свойства многообразий могут быть эквивалентными. Например, возможны два совершенно не похожие друг на друга многообразия, которые обладают одной и той же эйлеровой характеристикой. Это полезно, потому что вместо изучения сложных многообразий можно изучать простые. Однако очень трудно выяснить, какие свойства являются у двух произвольных многообразий общими. Оказывается, что если есть два многообразия, X и Y, то если построить их классы K0[X] и K0[Y] и специальным образом отобразить их друг в друга, то можно будет довольно простой проверкой, чуть ли не тупыми вычислениями, находить у многообразий общие свойства.
Это специальное отображение между K0-классами многообразий называется функтором K0. Кроме K0, существуют ещё функторы K1, K2 и даже Kn, чем больше n, тем навороченнее. Изучение функторов K называется K-теорией. Грубо говоря, K-теория - это изучение соотношений между разбиениями многообразий на карты.
Алгебраическая K-теория изучает функторы K, используя их чисто алгебраические свойства. Например, K0[X] является абелевой группой, что даёт возможность использовать теоретико-групповые инструменты. Ещё есть топологическая K-теория, использующая методы из общей топологии.
В частности, с помощью K-теории можно выяснить, насколько форма вселенной напоминает жопу твоей мамаши, путём изучения отношений между картами вселенной и картами жопы.
Упс, линк поставить забыл.
->
->
Например потому, что по твоему определению функция 1/x непрерывна в нуле.
> доопределённая чем-нибудь в нуле
Немного пофиксил.
Вроде, надо детей учить, но уже блевать тянет от этих глупых уженешкольников, набежавших на раздел с началом учёбы.
В конце обязательно надо было добавить незрелую идиотскую шутку. Гыгыгыг, как смищно.
Опчик, а поясни зачем вообще рассматривать векторные расслоения и что они могут сказать о многообразии без K-теории? И задачник по топологии, касающийся всей этой темы с накрытиями, расслоениями и как с помощью них можно считать фундаментальную группу?
Начнём с того, что это охуенно.
Смысл примерно такой же, как изучать карты земной поверхности вместо непосредственного изучения самой Земли. Изучение векторных расслоений - это способ изучать топологические (и не только) инварианты многообразий, которые, концептуально, объясняют, какие вообще многообразия возможны, а какие - нет. У этого могут быть самые разные приложения - описание того, какие решения у систем уравнений могут быть, какой формы молекулы могут существовать в реальности. Пока что этих приложений мало, но, возможно, в будущем будет больше.
Для начала полезно прочитать книжку Вербита по топологии, а потом книжку Атьи по K-теории.
Рудин
Возьмем функцию f(x) = x^2 в точке 2. Из того, что f(x) рядом с 4, не следует, что x рядом с 2, он может быть и рядом с -2.
Я тут задачу принес.
> Пока что этих приложений мало, но, возможно, в будущем будет больше.
Дооооо-дооооо.
В смысле? Касательное расслоение, кокасательное векторные расслоения, внешние степени кокасательного являются векторными расслоениями. Когерентные пучки являются обобщением векторных расслоений, а это уже пуп земли.
>И задачник по топологии, касающийся всей этой темы с накрытиями, расслоениями и как с помощью них можно считать фундаментальную группу?
Виро.
Не совсем в тему, но все же. Математическое образование в Европе(особенно интересуют Франция и Германия). Какие учебные заведения лучшие в этой сфере? (только pure, applied не рассматривается)
Во Франции эколи (Normale, Polytechnique). В Германии зависит от того, в чем хочешь специализироваться.
Но вообще, видимо, лучше в Бонн, там сразу институт Макса Планка и центр Хаусдорфа.
А эта эколь... как ее... Горная Школа... там же чистой математики нет?(вообще какое-то мутное, как по мне, заведение, которое почему-то считается престижным)
Оно Европейское, а значит не может быть мутным по определению Европейского.
Смущает то, что по ходу там ОЧЕНЬ мало студентов и почти все они postgraduate. на рейтинги не ориентируюсь, но в некоторых оно просто-напросто отсутствует. Математика там вроде как есть, но только в сугубо прикладных вариантах, а может и ошибаюсь....
А Техническая Школа Цюриха? Существенно хуже Бонна и Эколей?
И заодно... кроме мехмата и матфака вшэ, в этой стране жизни вообще нигде нет?
SUP, /math/. Поясни мне пожалуйста где я ошибаюсь. На пике я попытался посчитать значение преобразования Фурье от синуса в точке омега = 0, однако получил расходящийся интеграл. Что я сделал не так?
Кому не сложно, перечислите самых-самых из ныне живущих и российских математиков. Живущих и у нас и за рубежом- не принципиально.
Перельман.
Воеводский, Окуньков, Концевич
Кек, тут скорее не по лучшести смотреть надо. Бонн - новый Стамбул (тот же Мюнхен намного менее занят турками), Париж - новый Алжир, Цюрих в этом планее выгоднее смотрится, хоть и жить там охуеть как дороже.
Вербитский, Каледин, Манкунян.
Помогите с этим, посоны.
>Манкунян
>Прочитал сперва как маня-кун
Чёт я обдвачивался совсем
Вроде там часто интеграл понимают этот "в смысле главного значения". Т.е. берут предел не по всем отрезкам, а толька вида [-a, a]. По таким у синуса ноль при любом a.
Ноль и получается, в чем проблема?
А, ну типа интегрируют кусками равными периоду синуса? А если там sin(1.1x) + sin(x) под интегралом стоять будет? По какому периоду интегрировать?
В том, что интрегал от синуса по бесконечной области не сходится. Даже вольфрам об этом знает.
Так, про главное значение я прочитал http://femto.com.ua/articles/part_1/0807.html
Для синуса все норм, если интегрировать по [-а, a]. Что насчет косинуса и функций не четных и не нечетных? Для каждой свой предел выдумывать, чтобы интеграл сходился? Как-то это костыльно выглядит.
Может дело в том, что у некоторых(периодических) функций - спектр дискретный(юзаем ряды, а не интеграл), а у непериодических - непрерывный?
Вот и получается - что интеграл для "непрерывного" Фурье неопределен - юзай ряды Фурье, сцуко(там получится должен голый синус, что и подал на вход).
Простите, если хуйню спизданул.
>sin(1.1x) + sin(x)
Разбей на сумму интегралов.
> Что насчет косинуса и функций не четных и не нечетных?
Не нечетная и не четная представляется в виде суммы четной и нечетной.
>Для каждой свой предел выдумывать, чтобы интеграл сходился? Как-то это костыльно выглядит.
Не костыльно - используй свойства преобразования. На википедии из этого выводится.
>Не нечетная и не четная представляется в виде суммы четной и нечетной.
На счет четной функции не понял. Интеграл косинуса даже на [-а, a] не определен.
>На википедии из этого выводится.
Можно ссылочку?
>Не костыльно - используй свойства преобразования.
Нет костыльно. Вместо определения общего понятия для всех случаев, вы математики говорите, что тут надо делать так, там по другому, а в третьем случае по третьему. Говно короче какое-то.
>Можно ссылочку?
https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A4%D1%83%D1%80%D1%8C%D0%B5#.D0.92.D0.B0.D0.B6.D0.BD.D1.8B.D0.B5_.D1.84.D0.BE.D1.80.D0.BC.D1.83.D0.BB.D1.8B
Как видишь, там сначала ищется куча свойств этого интеграла, а из них уже быстро находится нужные, в т. ч. синусы и косинусы. Интеграл самому при этом брать вообще не нужно.
Точно так же, как производные ты находишь не через определение производной, а используя определенные символьные преобразования.
>Нет костыльно. Вместо определения общего понятия для всех случаев, вы математики говорите, что тут надо делать так, там по другому, а в третьем случае по третьему. Говно короче какое-то.
Такое часто бывает с бесконечностями, правило Лопиталя, к примеру. Не просто так некоторые их не переваривают. А я не математик, а инженер, мне достаточно того, что это работает.
Поясню - у синуса частотой 1 образом являются две точки для w=1 и -1. Для прочих частот(включая 0), амплитуды не определены.
Это, видимо, потому что при значениях 1/-1 там получается магия Эйлера(используй представление для синуса) - экспоненты рассасываются и получается интеграл, имеющий численное значение, а не неопределенность aka NaN.
Проверь на листочке мою гипотезу.
Почему не определены? Они строго нулю равны.
Дельта-функция является магической, потому что это https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D0%BE%D0%B1%D1%89%D1%91%D0%BD%D0%BD%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F
Может там с помощью какой-то высокоуровневой поеботы невычисляемый интеграл превратили в дельта-функцию в обобщенном смысле? Можно же сумму несходящегося ряда(сумма натуральных чисел) с помощью магии привести к -1/12(через функцию Римана или как там). Формально будет правильно.
тем более, что "локально"(на конечных числах) интеграл имеет смысл, на бесконечностях - нет. Там-то и нужна магия.
Вот я что подумал - т.к. синус периодический, мы можем перейти к конечным пределам интеграла с шагом его периодичности - тогда всё будет нормально. А если не юзать это свойство - получится неопределённость. Для нас лучше когда её нет, поэтому наше решение правильней и лучше ха-ха.
Неопределенность - это не решение. В отличие от бесконечности, к примеру.
Для предела(а значит и для несобственного интеграла) - это решение. Т.е. предела функции просто не существует - что верно для косинуса/синуса бесконечности - они болтаются вокруг 0 до бесконечности и никуда не сходятся.
Дак чего получается, посоны? Говно это ваше непрерывное преобразование Фурье? Срочно перекатываемся на его дискретный вариант?
Не говно, но из него подтекает нехорошая жидкость коричневого цвета.
Я вот тут подумал. А нет-ли какого-нибудь неподтекающего оператора, действующего на f(t) и на e^-jwt? Ну чтобы по нормальному ноль получался.
Так чем тебя не устроил этот вариант? Формально это будет выглядить так - возьмем интеграл по переменным пределам и перейдем к интегралу с ограниченными каким-либо отрезком(его длина=периоду) пределами(н-р 0<=x<2pi). Пределы вычисляются по тривиальным формулам(отбрасываются полные периоды по которым интеграл=0). Тогда мы "обобщим" интеграл по бесконечностям(неопределенный) до нашего определения(как делают с прерывными функциями в точке - дополняют в этих точках значением). Значение интеграла будет зависеть только от остатка деления длины отрезка интегрирования на период синуса/косинуса 2pi.
Т.е. несобственный интеграл мы будем считать для пределов 0 и 2*pi(т.е. считаем что пределы интеграла ходят от фиксированной точки=0 с шагом=периоду, иначе будут получаться разные значения). Тогда у нас всё будет ОК.
> Интеграл косинуса даже на [-а, a] не определен.
В каком смысле? Очень даже определен и численно равен 2*sin(a).
тред не читай сразу отвечай
В каком смысле? Очень даже определен и численно равен 2*sin(a).
тред не читай сразу отвечай
а на бесконечностях? В определении фигурируют они. Тут в этом вся соль.
При a -> inf я имел в виду
>Пределы вычисляются по тривиальным формулам(отбрасываются полные периоды по которым интеграл=0). Тогда мы "обобщим" интеграл по бесконечностям(неопределенный) до нашего определения(как делают с прерывными функциями в точке - дополняют в этих точках значением). Значение интеграла будет зависеть только от остатка деления длины отрезка интегрирования на период синуса/косинуса 2pi.
Почему это натуральным образом не появляется при выводе формулы для преобразования Фурье? Почему эти нюансы приходится обходить искусственно? Мне кажется это странным.
Я тут чего подумал-то, посоны. А ведь в ПФ t - комплексная величина в общем случае. Не расширяет-ли это понятие интеграла каким-либо образом? Я в универе проебал все лекции по интегралам комплексных функций, кажется.
помогите решить
>t - комплексная величина в общем случае
нет, действительная и интергал берется в смысле Коши/в смысле главного значения
>нет, действительная
Врёти https://en.wikipedia.org/wiki/Fourier_transform#Complex_domain Но чаще она конечно действительная, да.
> В том, что интрегал от синуса по бесконечной области не сходится.
Может я че-то не так понимаю?
Кто тебе сказал, что сумма последних двух членов равна нулю? Алсо, попробовал бы ты сделать это в мечети с косинусом!
Самое первое равенство не верно: слева интеграл сходящийся в смысле главного значения офк, а справа два расходящихся интеграла.
Так что такое "тензор" на самом деле?
>интергал берется в смысле Коши/в смысле главного значения
Ок, с синусом такая хуйня прокатывает. Про косинус что скажешь?
>can be studied for complex values of its argument "E"
переменная интегрирования "t" а не "E" действительная, иначе не имеет смысла запись пределов интегрирования от -inf до +inf
Расходится
набор функций
И что делать теперь? Должен быть ноль при омега = 0, а у нас интеграл расходиться. Вообще охуеть. Пиздят получается математики-то?
Ну да, а нашем-то случае это так. Только мне всё-равно от этого не легче.
>в нашем случае
А в каком случае в ПФ другие пределы интегрирования? ни в каком
Этот переход верен, только если все интегралы сходятся, а не абы когда.
>А в каком случае в ПФ другие пределы интегрирования?
В случае комплексной функции у него на входе?
функция под интегралом может принимать комплексные значения, но интегрирование идет по действительным числам
Ну ладно, просто у меня получается, что F(sin(0)) = 0, а у тебя получается, что F(sin(0)) не определено.
элемент тензорного произведения
Я попутал, кароч. Линк тебе неправильный дал. Там о частоте комплексной речь идет. А есть еще вариант, когда именно сигнал на входе комплексный. ЦОСовики даже применять это где-то умудряются. Модуляция у них там какая-то, хуё моё.
Знаю, что платина, но почему математики верят в результат 1 + 2 + 3 + ... = -1/12? Как они определяют сумму ряда? Я знаю только одно определение суммы ряда (предел последовательности частичных сумм), но оно, очевидно, здесь не подходит.
Ещё один. Рудин, блядь, для новичка. Что бы там эстетствующие бляди не говорили, но Фихтенгольц - лучший учебник по математическому анализу на русском языке.
А в чем проблема Рудина? Теория там дается вполне понятно. Сложность упражнений высокая, это да, но, во-первых, есть солюшн мануал, а во-вторых, можно читать только теорию, а задачи решать те, которые дают в универе.
тоже 0 получается, просто нужно интеграл от -inf до +inf не разбивать на два, а брать в смысле главного значения
не знаю, чтобы разобраться время надо
Сигнал - это f(x) может быть комплексным вполне как функция из R в С и интегрировать всеравно будем от -inf до +inf
>Теория там дается вполне понятно.
Для ньюфага-первокура нихуя непонятно. Сравни введение вещественных чисел у Фихта и Рудина. Также Рудин некоторые "мелкие" теоремы не доказывает ( ведь "очевидно"), делает скачки в доказательствах. Я вообще не пойму, схуя эту книжку считают учебником. Традиция непрерывного мат образования со школьной скамьи у нас прекратилась и поступают на математику люди вообще лишённые какой-лидо мат культуры.
>всеравно будем от -inf до +inf
Похоже ты прав.
>не знаю, чтобы разобраться время надо
Давай вместе разбираться, няша.
Поясните за пикрелейтед (это из учебника Munkres: Topology). Тут опечатка или че? Наверное, у меня просто проблемы с переводом. Я так понимаю,
> Let X and X' denote a single set in the topologies T and T', respectively
означает, что X ∈ T и X' ∈ T'. Но это не дает никакой информации о топологиях на X и X'. Аналогично, у нас нет никакой информации о топологиях на Y и Y'.
> Let X and X' denote a single set in the topologies T and T', respectively
означает, что X ∈ T и X' ∈ T'. Но это не дает никакой информации о топологиях на X и X'. Аналогично, у нас нет никакой информации о топологиях на Y и Y'.
я подумаю, вечером поспрашиваю людей, если что узнаю отпишу
Спасибо тебе
> Для ньюфага-первокура нихуя непонятно. Сравни введение вещественных чисел у Фихта и Рудина
Ньюфагу-первокуру можно не знать о построении вещественных чисел. Пикрелейтед - то, что написано у Рудина. Построение вещественных чисел вынесено в апендикс, потому что это чисто формальное упражнение для любителей оснований, польза от такого построения сомнительна.
Алсо, Фихтенгольца я не читал, не знаю хороший ли это учебник.Я просто предлагаю то, что мне самому понравилось. Кроме Рудина пробовал читать Спивака, но очень быстро заебался, потому что упражнений там очень много, упражнения однотипные, а теория дается как-то некрасиво, по-инженерному.
> Традиция непрерывного мат образования со школьной скамьи у нас прекратилась и поступают на математику люди вообще лишённые какой-лидо мат культуры.
Ну тогда надо сначала решать листки для 8-9 класса, которые называются "Элементы математики в задачах". Годнота же.
Я надеюсь ты понимаешь, что тензорность объекта следует жесточайшим образом отличать от его числовых значений. Это именно то место, которое множится в хреновых книжках, когда пишут заклинания про типа "тензор - это набор чисел, преобразующихся ...". За такие фразы пора давно руки отсекать. Также как и про "набор функций, преобразующихся ...". Аналогичную "ахинею" можно воочию наблюдать про эпсилон- тензор у ландавшица. Это утверждение, конечно не объявляет, что они не понимали, что такое тензор. Но то, что они пропопугайничали типично оканемевшие заклинания про его определения - это точно.
Похоже, тред заметно оживился. Здорово.
сейчас будет немного(а кому-то может и много) теории из матана, часто про такие вещи забывают
Во первых интеграл Фурье и преобразования Фурье вводятся для "абсолютно интегрируемых функций"(обозначается как "L").
Давай разберем, что это значит: (рис. 1 верхняя чать) я поясню кратко, если определение непонятно, могу полностью его словами написать
Мы берем некий отрезок [a b] из расширенной числовой прямой (R плюс +inf и -inf), второе условие требует, чтобы на этом отрезке сходился необходимый интеграл (рис 2.)
Если мы возьмем отрезок [-inf,+inf], найдем особые точки: {-inf;+inf}, вычтем из отрезка особые точки: [-inf,+inf]\{-inf;+inf}=(-inf,+inf), зададим функцию f(x)=sin(x) или f(x)=cos(x), как функции из (-inf,+inf) в R.
Мы получим функция, которая НЕ является абсолютно интегриреумой на отрезке [-inf,+inf], т.к. интеграл из 2-го условия не будет сходится (прошу обратить внимание на то, что под интегралом функция по модулю), сходиться интеграл не будет потому, что он будет неограниченно расти при уменьшении дельта-окрестности особой точки.
Теперь разрешение вопроса: в жизни не рассматриваются функции из (-inf,+inf) в R, а обычно рассматриваются промежутки, например сигнал принимался 10 минут, т.е. функция сигнала определена как функция из отрезка [0, 10 минут] в R. Если мы берем обычный отрезок и реальную функцию, то она всегда является абсолютно интегрируемой. Тот же cos или sin всегда будет абсолютно интегрируемый если рассмотреть конечный отрезок.
P.S. пришлось поднимать записи лекций по матану, освежил память немножк :3
Когда речь зашла об анализе. Совпадение?
Здесь X,Y и X',Y' это одни и те же множества (соответсвенно), но с разными топологиями. Ничего кроме этого тебе знать не надо.
>Теперь разрешение вопроса
>в жизни не рассматриваются функции из (-inf,+inf) в R, а обычно рассматриваются промежутки
Ну охуеть ты вопросы решаешь. Если уж переходить к жизни, то и непрерывным преобразованием Фурье никто не пользуется - везде ДПФ считают. Алсо в определении ПФ нет ничего про интегрирование по отрезку. Там ясно и четко проставлены бесконечности в качестве пределов.
Да, пределы интегрирования от -беск до беск, лишь бы функция была абсолютно интегрируема.
Но косинус-то у нас не абсолютно интегрируемый. А его фурье-образ существует. Как так?
Короче, видимо подставлять omega=0 и далее считать интеграл - неправильно. Тогда
http://dsp.stackexchange.com/questions/11554/obtaining-the-fourier-transform-of-cosine-and-sine
Тфу. Блядский харкач. Короче, поставлять omega=0, и считать интеграл методами школьного матана неправильно. Так ничего не насчитаешь. Вся магия находится в дельта-функции, которая вовсе не функция (impulses are defined only in terms of how they behave as integrands in an integral). Поэтому результат преобразования Фурье от косинуса - не функция, а обобщенная функция. И вот в нее уже можно подставить omega=0 и получить результат.
Вот здесь на пикрелейтед преобразование Фурье косинуса вычислено как сумма двух дельта-функций. Вроде бы мы можем подставить a=1, omega = 0 и получить ответ (0). Но на самом деле нет.
From a purely mathematical viewpoint, the Dirac delta is not strictly a function, because any extended-real function that is equal to zero everywhere but a single point must have total integral zero.[6] The delta function only makes sense as a mathematical object when it appears inside an integral.
То есть брать преобразование Фурье косинуса и подставлять omega = 0 - это нонсенс. А сам такой интеграл невычислим.
From a purely mathematical viewpoint, the Dirac delta is not strictly a function, because any extended-real function that is equal to zero everywhere but a single point must have total integral zero.[6] The delta function only makes sense as a mathematical object when it appears inside an integral.
То есть брать преобразование Фурье косинуса и подставлять omega = 0 - это нонсенс. А сам такой интеграл невычислим.
>И вот в нее уже можно подставить omega=0 и получить результат.
Не, нельзя.
Не, нельзя.
Пытаюсь решить пикрилейтед. Какий матрицы (в явном виде) удовлетворяют учловию X=X^-1? Интуиция (лол) подсказывает, что это - единичная матрица. Если это верно, то как доказать формально? Подозреваю, что в условии не зря сказано про вещественные матрицы. Нужно рассматривать группу (кольцо? поле?) и из ее свойств выводить следствие, что если X=X^-1 то X=E. Помогайте, знатоки линейной алгебры. Просьба в ответе кинуть ссылкой на литературу, если не затруднит.
Анализ тут не причем. Просто сентябрь, учебный год начался. Школота и студентота подтянулись в тред со своими УМОЛЯЮ РЕШИТЕ!!11
>X=X^-1
Мне лень чего-то думать, но разве любое вращение на пи (вокруг любой оси) не подойдёт?
Просто немножко обобщили и оформализовали, поразмахивали руками(как в случае с несходящимися рядами) - и стало всё аккуратно и ничего не подтекает.
там объясняется что можно посчитать наоборот(из дельта-функций в косинус). Любопытно стало, можно ли "впилить" дельта-функции при прямом преобразовании(наверняка какое-то простое тождество для функции Дурака(цитируя отечественного классика) нужно)?
Ловкость рук и никакого мошенничества©.
>нужно рассматривать группу кольцо
можешь еще алгебру рассмотреть или вспомнить 8ой класс и простые методики доказательства.
Лел, а с чего ты взял, что X^-1 вообще существует?
>X=-X^-1
>X=(-1)^(-1)X^(-1)
>X=X^(-1)
Вот с этого проиграл.
Тааакс что тут у нас? Смотрим на второе равенство - протранспонируем его, получим что X транс. тоже удовлетворяет уравнению - значит матрица X симметричная.
Докажем, что матрица X - диагональная. Допустим, что это не так(существует не-0 диагональный элемент - допустим на ячейке i, j). Запишем элемент матрицы X^2 для ячейки i, j - т.к. матрица симметричная у нас там будут квадраты элементов X которые больше 0.
Дальше продолжать, курсант?
X = -X^-1.
Это вращения на pi/2 вокруг всевозможных осей.
Тащемта достаточно определители от обеих частей X^2=-E взять.
> т.к. матрица симметричная у нас там будут квадраты элементов X которые больше 0
Умножение матриц на скиле.
Кстати, я забыл упомянуть, что я оперся на факт X^2=Y^2 => X=Y, уверь меня в этом - или всё доказательство летит к чёрту.
>Смотрим на второе равенство - протранспонируем его, получим что X транс. тоже удовлетворяет уравнению - значит матрица X симметричная.
Вообще непонятно это «значит», кстати. А если бы были матрицы 2х2 твоё рассуждение как бы изменилось?
Вообще непонятно это «значит», кстати. А если бы были матрицы 2х2 твоё рассуждение как бы изменилось?
А, не, не то.
Поясняю (X_t)^2=-E=X^2. Отсюда пытаемся делать вывод что X=X_t
Поцчему? То. Только вопрос в том, есть ли другие решения.
На каком основании?
Вывод x^2=a=y^2 -> x=y даже в вещественных числах не верен.
>1
>>>296408
>Поясняю (X_t)^2=-E=X^2. Отсюда пытаемся делать вывод что X=X_t
Видимо для благороднох донов определитель от обеих частей взять () — импосибиру проблем, ну что же, ладно.
Это было бы тем, но только над комплексными, и то если чуть-чуть подправить домножением на i векторов оси. Как выше заметили, над вещественными таких матриц нет конечно же.
Обратная матрица существует т.к. если взять определитель X^2=E => определитель X=1. Что полезного можно извлечь из неё?
Но ведь из x^2=y^2 -> для модули x и y. Может тогда верно что из X^2=Y^2 => для модулей элементов X=Y?
Определитель это мемы. Тогда уж можно и собственными векторами ебануть сразу.
да, обосрался слегка
ок, буду копать в сторону симметических матриц
Не понял при чём тут мемы и собственные вектора.
»»»_««« Ну что же, удачи.
>симметических
симметричная, офк
бля, ати
Определитель это типа чит прост, так неинтересно.
Понятия не имею что такое модуль матрицы. Но если матрица nxn (над полем комплексных чисел) диагонализируема, то она имеет 2^n корней.
Это всё хорошо, только в задаче было написано найти те, которые X^2=-E (что сути не меняет конечно, ибо об элементах пустого множества любое утверждение верно).
|X| это все Y такие что Y*Y=X
>YY=XX
я имел в виду то, что модули элементов матриц на ячейках i,j равны для матриц у которых X^2=Y^2. Всего лишь догадка.
А если в лоб записать квадрат матрицы? Там нужно чтобы для любых недиагональных элементов были = 0. Допустим, что где-то один не-0 элемент. Тогда у нас при одном и только 1 не-нулевом элементе на том же месте будет не-ноль. Добавим по приколу еще один элемент - пронюхивается математическая индукция. Если элемент будет на другом столбце-строке добавится еще 1 не-ноль в результирующую матрицу. Если же на ту же строку-столбец - то...
> А если в лоб записать квадрат матрицы?
Хинт: запиши любой элемент на диагонали квадрата симметричной матрицы.
Я вообще не в терминах определителей рассуждал, а в терминах ориентаций: дескать любое линейное невырожденое преобразование либо сохраняет ориентацию, либо меняет её. Если X меняет ориентацию, то X^2 сохраняет (меняет два раза), а -Е, очевидно, меняет.
Но это тоже самое, конечно.
Странное какое-то определение, у тебя модуль — это множество? В любом случае у матриц {{0,0},{0,0}} и {{0,1},{0,0}} равны и «модули» и квадраты.
Тот же самый пример, что и выше.
В общем, с симметричностью чё-то проблемы - может если покопаться получится.
Кстати на - ошибка. Минус вынесен из-под обращения матрицы, хотя он применялся после обращения матрицы. Так что там будет X=-X^-1. Единичная матрица не подходит, по оригинальному условию, но матрица с мнимыми единицами по диагонали вполне - но это уже выход из действ. чисел.
Решений в действительных числах нет и надо это доказать.
По условию т.к. определитель X = 1, то в ней нет нулевых строк/столбцов.
твой пример опровергает гипотезу для всех матриц. А если попробовать найти контрпример среди матриц без нулевых строк/столбцов?
Также можно попробовать записать обратную матрицу явно через алгебраические дополнения и воспользоваться тем фактом, что нулевых строк/столбцов нет.
В общем, самое простое(и пока единственное) решение - - простое доказательство того, что таких матриц нет в действительных числах(квадрат определителя = отриц. числу для нечетной размерности).
Кстати на - ошибка. Минус вынесен из-под обращения матрицы, хотя он применялся после обращения матрицы. Так что там будет X=-X^-1. Единичная матрица не подходит, по оригинальному условию, но матрица с мнимыми единицами по диагонали вполне - но это уже выход из действ. чисел.
Решений в действительных числах нет и надо это доказать.
По условию т.к. определитель X = 1, то в ней нет нулевых строк/столбцов.
твой пример опровергает гипотезу для всех матриц. А если попробовать найти контрпример среди матриц без нулевых строк/столбцов?
Также можно попробовать записать обратную матрицу явно через алгебраические дополнения и воспользоваться тем фактом, что нулевых строк/столбцов нет.
В общем, самое простое(и пока единственное) решение - - простое доказательство того, что таких матриц нет в действительных числах(квадрат определителя = отриц. числу для нечетной размерности).
Довольно простое решение без определителей, но с транспонированием и симметричными матрицами
Не, не множество, там еще есть ограничение на вид матрицы. Короче модуль - это корень из квадрата матрицы.
>твой пример опровергает гипотезу для всех матриц. А если попробовать найти контрпример среди матриц без нулевых строк/столбцов?
{{1,1},{0,1}} {{1,0},{0,1}}
Пока нет, по хинту его востановить не смог (не исключаю, что я тупой).
Корень из квадрата матрицы не определён однозначно.
Если X = X^(-1), то X^2 = XX = XX^(-1) = E, а нам нужно -E.
>{{1,1},{0,1}} {{1,0},{0,1}}
Прошу прощения, протупил слегка во всяком случае над комплексными числами пример легко строится, над вещественными — ещё подумаю.
я уже указал на ошибку
, там будет X = -X^(-1)
как докажешь что X - симметрична?
>Поясняю (X_t)^2=-E=X^2. Отсюда пытаемся делать вывод что X=X_t
>Вывод x^2=a=y^2 -> x=y даже в вещественных числах не верен.
>Но ведь из x^2=y^2 -> равны модули x и y. Может тогда верно что из X^2=Y^2 => модули элементов матриц X и Y равны |x_ij|=|y_ij|?
Необосновано - надо обосновать либо симметрия идёт лесом.
Или я чего-то не понимаю?
Допустим, определил ты квадратный корень из матрицы и он однозначно определен. Но как его считать? Можно конечно загнаться и попробовать перенести численный метод Ньютона для вычисления корня с вещественных чисел но хз - получится ли и будет ли толк.
(XY)^t = (Y^t)(X^t)
Фуф, даун-первокур ворвался.
Задание - выделить действительную и мнимую часть. У меня говно какое-то выходит. Хелп.
Задание - выделить действительную и мнимую часть. У меня говно какое-то выходит. Хелп.
Настало время охуительных чудес!
Чет не понял. Надо двойку заменить или что?
Решение по идее должно быть совсем простое, так как это задание номер 1, лол.
Домножь на комплексно сопряженное (2+5i) числитель и знаменатель, избавишься от i в знаменателе. 2. Распиши экспоненту через формулу Эйлера еxp(x)=cos(x)+isin(x). Далее раскрой скобки и выдели часть без i и
Спасибо. Вроде и понятно было, но тупил.
Какая есть очень мягкая теория чисел?
Пустое множество, если я тебя правильно понял ;)
ну ок, а что там тогда помягче, если конкретно?
Во-первых ты неправильно преобразовал. Условие X^2=-Е, а не Е.
Таких вообще нет с заданными условиями, так как есть вещественное собственное значение, у квадрата будет квадрат собственного значения, а он положителен.
Условие же X=X^(-1) для матрицы произвольного порядка над полем характеристики не два, это то же самое, что матрица диагонализуема с собственными значениями +/-1. Такие очевидно подходят, так как в квадрате тождественны. Другие не подходят, так как в алгебраическом замыкании есть жорданова нормальная форма, а квадрат жордановой клетки единичен только если это просто собственное значение +/- 1.
Все кто писал выше ничего не знают, забудь все, что они сказали.
>Интуиция (лол) подсказывает, что это - единичная матрица.
>Нужно рассматривать группу (кольцо? поле?) и из ее свойств выводить следствие, что если X=X^-1 то X=E
Конечно, нет.
А еще все кто писал выше ничего вообще не знают, не слушай их.
Ой. Не все. Прошу прощения у тех, кто до этого писал правильное решение для X^2=-Е.
e^ix = cos x + i sin x. Ставишь сюда вместо икса тройку, получаешь нормальную форму записи. Потом числитель и знаменатель домножаешь на сопряженное к знаменателю (2 + 5 i). В числителе перемножаешь два комплексных числа, в знаменателе образуется вещественное число, на него делишь вещественную и мнимую часть того, что получилось в числителе. ПРОФИТ
>твой пример опровергает гипотезу для всех матриц. А если попробовать найти контрпример среди матриц без нулевых строк/столбцов?
{{1,0},{0,1}}, {{-1,0},{0,-1}}
Анончик, помоги решить. Я уже весь потом изливаюсь, все перепробовал, но даже близко не подошел к ответу.
Тут работает равенство для любых i,j |aij|=|bij|, как я и преполагал. Надо опровергнуть это - либо попытаться доказать(мне в лом чёт ;).
Разложи 2015 по степеням двойки.
2015 = 1024 + 512 + 256 + ...
Сначала находишь (1 + sqrt(3))2. Потом
(1 + sqrt(3))4 = ((1 + sqrt(3))2)2
(1 + sqrt(3))8 = ((1 + sqrt(3))4)2
и т. д.
Всего таких действий у тебя будет не больше чем log22015, то есть примерно 11. Потом перемножаешь нужные степени.
В принципе, все эти операции можно сразу делать по модулю 1, но я тебе предлагаю посчитать точный результат в виде a + b*sqrt(3), потому что тогда погрешности не будет.
Если не понял, гугли алгоритм быстрого возведения в степень.
Да проще прогу напиши, там всего-то 2015 операций. То есть на n-м шаге у тебя есть выражение вида (a + bsqrt(3)).
(a + bsqrt(3))(1 + sqrt(3)) = (a + 3b) + (a + b)*sqrt(3).
То есть
an+1 = an + 3bn
bn+1 = an + bn
Тебе потребуется длинная арифметика, чтобы получить b.
> можно сразу делать по модулю 1,
Нельзя, потому что, например
3 == 1 mod 1
но
3sqrt(3) = 5.19615242
1sqrrt(3) = 1.7320508
Придётся делать полные расчеты, а там числа по несколько сотен десятичных знаков. И их придётся хранить полностью.
Саентачане, посоветуйте годных книжек по диффурам и теормеху.
https://drive.google.com/open?id=0BxD1_CQGaoa4YWFqWW5vUHZjbDg
https://drive.google.com/open?id=0BxD1_CQGaoa4YWFqWW5vUHZjbDg
Попробуй, но преподавателя это конечно не заменит
Лол. Я сначала написал прогу на питоне, которая решает задачу для любой степени и корня (на моём компе работала примерно 15 секунд), а потом понял, что задача решается на бумажке.
Хотите решить сами - под спойлер не смотрите и программу не запускайте.
Программа использует только целые числа (длинные, конечно же), никакого floating-point, так что ответ точный. http://pastebin.com/2egk0L6K
А теперь самое интересное: результат и как получить решение на бумажке.
Так вот, первые 10 цифр это 0000000000.
Я сначала охуел. Потом проверил для малых степеней (всё ок). А потом сделал фейспалм и сказал: ну конечно же, числа Пизо, как я мог о них забыть
hint: искать разности чисел
Не совсем понял твой хинт. Мой хинт (если лень читать про числа Пизо)
рассмотреть, чему равно (1+sqrt(3))^n + (1-sqrt(3))^n
Какой ЯП лучше для математико-ориентированных программ? Пока небольших, просто задачи вузика вроде моделирования различных случайных величин.
Сам только си/плюсы немного знаю, но понял что низкоуровневая ебля сильно мешает в таких задачах.
Сам только си/плюсы немного знаю, но понял что низкоуровневая ебля сильно мешает в таких задачах.
R
Зависит от того, какая математика, она сильно разная бывает.
Python + numpy охуенен.
> Python + numpy охуенен
Лолблеядь.
Вот это получше.
> моделирования различных случайных величин
Это что вообще такое?
А чё там с Хаскелем?
Лучше всего бери питон (numpy scipy и много чего еще). Сам я на матлабе, но это дело чисто привычки, питон имеет все то же самое и намного больше еще.
Если не любишь пердолиться в консоль и качественные мануалы, много dsp, image, audio processing - бери матлаб. Курс machine learning от Эндрю Ына как раз на матлабе.
R выбирают статистики. Он бесплатен.
Для символьных вычислений - mathematica. Правда, мне maple приятнее, но он менее мощный.
Статически-типизированный язык для мелких скриптов не очень удобен, да и готового кода под него очень мало. Если хочется попердолиться с типами и отсутствием библиотек, лучше взять Julia.
Уйди со своим Хаскелем. ООП не нужно.
Есть завтра какие-нибудь спецкурсы или семинары в дс кроме спектральной геометрии? То есть точнее сегодня уже, 12го.
фортран
> питон имеет все то же самое и намного больше еще.
Упитанно.
> Для символьных вычислений - mathematica.
Штука баксов или сколько она там сейчас стоит?
Это для весьма специфических целей. Если теоретическим компсаем занимаешься. Для реальных расчётов практически не применяется.
Познания о ФЯП уровня /sci/
Математикач, поясни мне за дифференцируемость функции от двух переменных в точке. Как установить, дифференцируема ли она в ней? На пальцах желательно.
На пальцах - попробуй погладить эту функцию пальцем в этой точке. Если она не колется и не чувствуешь разрывов и углов, а все гладенько - то дифференцируема.
>Упитанно
Ты школьник ебаный, а я этим зарабатываю
Ну антошка. Ну объясни нормально. У вас тут целый тред фанатов топологии.
Для статистики - R, для вычислений - LISP, для "практического примнения теорката" хашкель, для доказательств - Ада.
Дифференцируема тогда и только тогда, когда существуют частные производные по обоим аргументами.
Можешь авторов назвать, там зарегаться на гугле надо.
"низкоуровневый" лал. А теперь открываем для себя волшебный мир библиотек для C/C++
http://www.gnu.org/software/gsl/
C/C++ не для скриптов - но наговнокодить математическую программу с численными методами там тоже можно быстро - с использованием либ, конечно. Как бонус - шустрая производительность.
Но это же неправда.
a=sqrt(3)
(1+a)^n - (1+a)^(n-1) = (1+a-1)(1+a)^(n-1) = a(1+a)^(n-1) → ∞
Лолблеядь! Мои стороны! Бахаххахахахах. Что это за дыра такая, что может себе позволить только "Матлаб для нищебродов" (=нампай). Рашка что ли?
> для вычислений - LISP
Лолблядь. Остальное правильно.
Лучше не надо ребёнка направлять сразу на неправильный путь. Иначе блядские кресты так никогда и не умрут до конца.
В случае, если частные производные в точке обе равны нулю? Это норм? Я просто не понимаю как надо конкретно брать частные производные, подставлять у0 и искать производную по х и потом подставлять в функцию х0?
С игреком аналогично.
Просто у Письменного в учебнике написано что (x^2+y^2)^1/2 не дифференцируема в (0,0)
Но по факту когда подставим 0 и возьмем производную-получим единицу в производной по х, так же будет с производной по игрек.
Крестохейтер спалился. Какое тебе дело - полностью они умрут очень не скоро - если вообще умрут, вычислительные программы можно писать и на чистом C(с годными либами). Именно для вычислений скриптовые свистелки-перделки меньше всего нужны.
>Лолблядь
А какой еще язык лучше подходит для математических алгоритмов? Си что-ли? Да на си можно только биты ебать.
> Сагает в медленной тематике
Дебила-нюфаню за версту видно. Да ещё и байтоёб. Байтоёб хуже псиной мочи.
Математика - символьные операции, Матлаб - вычисления. Всё остальное - кривое говно для нищеёбов. Агды и коги - совсем другая история.
>учить уебищный жабаподобный яп
>платить за это
>2015
ahahaha
Матаны, объясните своими словами, что такое "предельная точка" и "предел числовой последовательности", пожалуйста. С меня как всегда.
Фу, бля, байтоёбским нищеёбом с парашкоНИИ пасёт, что аж глаза режет.
>Лучше всего бери питон (numpy scipy и много чего еще).
И пока накатишь и изучишь все нужные себе библиотеки, пройдет полжизни. Можно, конечно, накатить сборочку от Васяна, но ты сам понимаешь, каково это по сравнению с инструментом, где из коробки все есть и настроено на работу друг с другом. Прохожу курс по data analysis на dataquest'e, и проигрываю: сначала работали в numpy, и там обращение к элементам массива a[i, j], а потом стали работать в pandas, там они себе высрали вместо обычных массивов какую-то сущность dataframe, и обращаться к ней надо уже a.iloc[i, j]. Каждый чухан выдумывает для своей библиотеки свой велосипед, а ты потом запоминай, с каким говном как полагается пердолиться.
>Если не любишь пердолиться в консоль и качественные мануалы, много dsp, image, audio processing - бери матлаб.
Математика все это умеет, и мануалы там еще пизже.
>Курс machine learning от Эндрю Ына как раз на матлабе.
Ну да, там, типа, есть инструменты для этого, вот только когда мне надо было по-быстренькому сварганить генетический алгоритм, и я решил для этого попробовать матлаб, то выяснилось, что в матлабе нужного мне типа хромосомы (и, соответственно, мутаций, скрещивания, и т д) нет в стандартных, а если писать все это самому, то проще написать вообще все самому, нежели ебаться с петушиным матлабовским синтаксисом и ограничениями того инструмента - что я и сделал на питоне с нуля за то же время, которое потратил на чтение мануалов матлаба.
>R выбирают статистики. Он бесплатен.
Тут не знаю, не видел, но математика тоже может считать всякие матожидания с дисперсиями и строить очень красивые диаграммки и графики, так что сдается мне, что уже поэтому для 75% юзеров R математики хватит с головой.
Давно хотел выяснить вживую, чем математика хуже других пакетов. Давайте, тащите сюда задачи и их решения на своих недоинструментах, а я решу эти задачи в математике, и посмотрим, что лучше.
У С++ нет REPL (cling не всчет и ты все равно им не пользуешься), поэтому отладка долгая и муторная.
>Лолблеядь! Мои стороны! Бахаххахахахах.
Мамкин траль, ты заебал со своей клоунадой.
>Что это за дыра такая, что может себе позволить только "Матлаб для нищебродов" (=нампай). Рашка что ли?
В России у меня стоял матлаб с рутрекера. С этим-то проблем нет. Основная проблема матлаба в том, что это довольно специализированный язык. Матрицы перемножать хорошо, но как только тебе нужен natural language processing, к примеру, все становится в разы грустнее.
Ты о чем вообще? Матлаб появился раньше любой жабы, математика - это лисп.
Последовательность - это счётное число точек (возможно, совпадающих). Предел последовательности - такая точка, что в любой её окрестности лежат почти все точки последовательности (т.е. все, кроме конечного числа штук).
по линкам нет доступа
>И пока накатишь и изучишь все нужные себе библиотеки, пройдет полжизни.
Накатывается оно через sudo pip install имя. Это не проблема. Полжизни у тебя пройдет в любом случае, и тут у тебя два варианта - вкладывать свою жизнь в опенсорсный продукт или в проприетарный. Первое лучше.
>Математика все это умеет, и мануалы там еще пизже.
Жертва пропаганды на хабре. Нихуя математика не умеет. Полно пейперов, код которых выложен на matlab central. На математику всем плевать, потому что в рот ебали этот лисп.
>а если писать все это самому, то проще написать вообще все самому, нежели ебаться с петушиным матлабовским синтаксисом
Вот теперь ты на самом днище языкосрача, доебываешься до синтаксиса, то есть твоего узкого мозга не хватает, чтобы понять, что синтаксис - дело привычки. На этом я шлю тебя нахуй, программист, который не разобрался с ga toolbox. Пиздец, там в опции передаешь нужные тебе функции, который этот фреймворк вызывает, но нет, нужно гордиться велосипедостроением с такими дешевыми понтами, что охуеть вообще.
>Тут не знаю, не видел, но математика
Да нахуй иди со своей математикой.
Да математика норм. Жаль что создатель жадный пидор с комплексами.
матлаб может вроде как и в символьное исчисление
правда это вонючий неудобный лагающий кусок говна, ненавижу блджад
Все могут во всё, вопрос в том, кто во что может лучше.
>Накатывается оно через sudo pip install имя. Это не проблема.
Вся суть универсальных ЯП - установи установщик установщика, потому что в стандартном функционале нету нихуя.
>Полжизни у тебя пройдет в любом случае, и тут у тебя два варианта - вкладывать свою жизнь в опенсорсный продукт или в проприетарный. Первое лучше.
Для погромизда лучше думать, с чем бы попердолиться, а для меня лучше быстро решать задачи, которые мне интересны и за которые мне деньги платят. Я работаю с математикой еще с универа, и кроме того, что ОЛОЛО ШТУКА БАКСОВ, от проприетарщины я не увидел никаких минусов. В исходники
я все равно не полезу, все проблемы решаются средствами самого языка. Зато если бы он был попенсросный, в нем бы не было и десятой части нынешнего функционала, который притом пришлось бы собирать и настраивать через пип-хуип, ебаться с обновлением и совместимостью версий, со всем этим библиотекодерьмом. Потому что не было бы людей, которые были бы мотивированы на разработку качественного и удобного функционала так, как те, кому за это платят. Потому что не было бы людей, которые формируют цельный продукт, а не набор полуфабрикатов для васяносборочек.
>Жертва пропаганды на хабре. Нихуя математика не умеет.
>На математику всем плевать, потому что в рот ебали этот лисп.
Ох лол, кто еще тут жертва пропаганды? Сам-то хоть попробовал в математике что-то сделать, или только прочитал в комментариях какую-то хуйню про лисп, и сразу обрел мнение эксперта?
>Вот теперь ты на самом днище языкосрача, доебываешься до синтаксиса, то есть твоего узкого мозга не хватает, чтобы понять, что синтаксис - дело привычки.
Суть не в синтаксисе, а в том, что его долго и тяжело учить. То есть проблема в мануалах. В математике синтаксис еще более пизденячий, но учится он примерно как питон, потому что ты можешь найти и скопипастить рабочий пример, близкий к тому, что ты хочешь сделать, видоизменить его под себя, и после пяти таких проб ты уже запомнишь синтаксис.
>На этом я шлю тебя нахуй, программист, который не разобрался с ga toolbox. Пиздец, там в опции передаешь нужные тебе функции, который этот фреймворк вызывает, но нет, нужно гордиться велосипедостроением с такими дешевыми понтами, что охуеть вообще.
Вот именно, там все эти функции нужно создать и передать, ну так и на кой хуй мне это делать в говноматлабе, если все, что от функционала инструмента в этом случае осталось - это прогнать лупом n раз последовательность реализованных мною функций?
Говорю же, неси свои задачи на своих недоязыках, я покажу тебе, что математика умеет.
>Говорю же, неси свои задачи на своих недоязыках, я покажу тебе, что математика умеет.
http://www.ee.ic.ac.uk/hp/staff/dmb/voicebox/voicebox.html
Ты скажешь, конечно, МОЖНОЗДЕЛОТЬ, но это похуй, в лиспах всегда можнозделоть. А на деле матлаб всегда был стандартом для dsp, кодобаза огромная, и хоть ты усрись, никогда тебе твой стивенвольфрам ничего подобного не напишет.
https://reference.wolfram.com/language/guide/SignalProcessing.html
https://reference.wolfram.com/language/guide/SoundAndSonification.html
https://reference.wolfram.com/language/Audio/guide/AudioPackage.html
https://reference.wolfram.com/language/Music/guide/MusicPackage.html
Всякая поебень типа генерации случайных векторов и шума, которая относится не только к спич процессингу, есть в соответствующих мануалах, а у тебя придется при подключении двух пакетов выбирать, каким из велосипедов пользоваться.
И я просил задачу, которую можно сесть и закодить за часок, чтобы сравнить, а не либу.
От нескольких людей слышал о том что алгебраисту хорошо бы знать нормально функан и особенно хорошо обобщённые функции. Кто в теме, можете прокомментировать? В чём соль и при чём тут алгебра вообще?
В этом тулбоксе реализован код серии классических пейперов. Например,
Ephraim, Y. & Malah, D.0 Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator IEEE Trans Acoustics Speech and Signal Processing, 32(6):1109-1121, Dec 1984
То есть, бумаге почти 30 лет. На матлабе есть несколько реализаций. Твои ссылки - детский сад, самые базовые алгоритмы. Особенно похвальба дизайном фильтров, который в матлабе на 10 голов выше.
>И я просил задачу, которую можно сесть и закодить за часок, чтобы сравнить, а не либу.
Да я говорю, шел бы ты нахуй со своими велосипедами. Пока ты будешь в своем "удобном" инструменте реализовывать то, что давно написано на матлабе (или вообще ждать, пока стивенвольфрам через 30 лет что-то реализует), я напишу 2 строчки и пойду пить пиво. И ты еще утверждаешь, что "Для погромизда лучше думать, с чем бы попердолиться, а для меня лучше быстро решать задачи, которые мне интересны и за которые мне деньги платят.". Я-то лучше попердолюсь с существующим кодом пару часов, чем буду городить велосипеды.
>Потому что не было бы людей, которые формируют цельный продукт, а не набор полуфабрикатов для васяносборочек.
Наука - это всегда набор полуфабрикатов. В проприетарные пакеты всегда попадают только древние проверенные временем хуйни (читай - которые есть в учебниках) уже с десятком-другим open-source реализаций. То есть, практически нихуя не попадает. Как видишь, даже код из 80-х не всегда есть.
И тут есть разные ниши. Те, кто обрабатывают сигналы, сидят в матлабе с 80-х. Те, кто работает в интернете - с обработкой языка, краулерами, бигдатой - любят питон. Математика нужна тем, кто занимается символьными преобразованиями, как бы вольфрам не пытался впарить это как покупайте-мой-йоба-крутой-дсп-софт.
>Ох лол, кто еще тут жертва пропаганды? Сам-то хоть попробовал в математике что-то сделать, или только прочитал в комментариях какую-то хуйню про лисп, и сразу обрел мнение эксперта?
Лисп - это лисп. Можнозделоть что угодно, а на деле - костыль на костыле. Сравни, например A(:, 1) в матлабе (синтаксис, который невозможно превзойти, только повторить) с https://reference.wolfram.com/language/howto/GetPartsOfAMatrix.html
>Суть не в синтаксисе, а в том, что его долго и тяжело учить.
Суть в том, что у тебя синдром утенка и ты уже на дне, потому что доебаться не до чего и ты доебываешься до синтаксиса. У матлаба в своей нише синтаксис замечательный, а остальные языки или прут его как есть (типа julia) или пытаются сделать что-то подобное средствами языка (c++ armadillo и opencv, python - numpy и т. п.).
>от именно, там все эти функции нужно создать и передать, ну так и на кой хуй мне это делать в говноматлабе, если все, что от функционала инструмента в этом случае осталось - это прогнать лупом n раз последовательность реализованных мною функций?
Из всей аргументации у тебя тут "вместо матлаба я взял питон потому что матлаб говно". Дно.
>Твои ссылки - детский сад, самые базовые алгоритмы.
Тем не менее, они есть, со всеми удобствами решения "из коробки". Причем это я тебе показал только возможности встроенных средств языка, и еще даже не смотрел сторонние модули.
>Особенно похвальба дизайном фильтров, который в матлабе на 10 голов выше.
Ну уж наверное для более старой среды понапилено побольше всякого. Это никак не связано с тем, хороша или плоха среда сама по себе.
Хорошо, ты меня убедил, для решения задач, которые уже реализованы в инструменте, лучше этот инструмент, чем тот, в котором этого нет. Но это ничего не говорит о том, хорош сам по себе инструмент или плох. Просто в нем это уже есть. А если взять что-то, чего в матлабе нет?
Вот например. Я хочу воспроизвести исследование из этой работы http://eprint.iacr.org/2015/852.pdf , в частности, перепроверить тропические степени с 1й по 5ю матрицы A, которые приведены на страницах 2-3. Мне нужна реализация тропических операций сложения и умножения, которые описаны на странице 1. Могу уверенно сказать - это не реализовано ни в математике, ни в матлабе, ни в питоне/нумпи/хуюмпи - нигде, так что все в равных условиях. Где такое решение будет создать проще и пользоваться им будет удобнее?
В математике реализовать всю тропическую алгебру матриц - строчек 15 кода, причем вводить и выводить формулы можно будет с использованием нотации из статьи: ⊕, ⊗. То есть можно будет писать A⊗B⊕C, а не вырвиглазное tropicalplus(tropicaltimes(A, B), C). Матлаб может такое? А питон? Где будет удобнее работать и получать результаты, и как скоро?
>Сравни, например A(:, 1) в матлабе
A[[All, 1]]. Одна хуйня, я бы даже сказал, что ключевое слово All понятнее, чем птичий язык, что несомненно проявится в большой и непонятной программе. Пара скобок вместо одной - это отдельная тема для разговора, но вообще правило левой руки в математике - это обрабатывать массив целиком в функциональном стиле, а не дергать каждый элемент или строчку/столбец в процедурном for'о-говне.
>У матлаба в своей нише синтаксис замечательный
Возможно, я не инженер-байтоеб, и от меня эта ниша далека. Но тот факт, что я не смог за разумное время взять и написать хотя бы что-то рабочее, когда мне это нужно было, много говорит если не о синтаксисе, то о мануалах.
>Из всей аргументации у тебя тут "вместо матлаба я взял питон потому что матлаб говно". Дно.
Ты какой-то тупой. Я тебе подробно объяснил, что матлаб я не взял потому, что матлабовский инструмент сделает за меня 5% работы, а 95% я сделаю сам при любом раскладе. А поскольку матлаба я на тот момент не знал на необходимом уровне, мне это не дало бы никакого выигрыша.
В задании написано "Вычислить". Этого хватит, или еще надо? задание на 1, ответ на 2 пикче, лол
лучше всего sagemath, который основан на питоне
если будешь в церне работать - то учи фортран
если на вмк - то матлаб
будешь работать с теорией узлов - SnapPea - https://en.wikipedia.org/wiki/SnapPea
octave говорят говно
ещё есть mathematica, magma, r, maple
но ещё раз повторю
самое клёвое - это питон + библиотеки
или sagemath:
> SageMath is a free open-source mathematics software system licensed under the GPL. It builds on top of many existing open-source packages: NumPy, SciPy, matplotlib, Sympy, Maxima, GAP, FLINT, R and many more.
>Возможно, я не инженер-байтоеб, и от меня эта ниша далека.
В итоге все свелось к "Математика - универсальна, а кому она не подходит - те байтоебы". Signal processing никакого отношения к байтоебству не имеет. Я с самого начала писал (), что вопрос в нише, а ты, фуфлыжник, начал пиздеть о якобы универсальности вольфрамоговна. В остальном ты так же скучен, как и твоя дешевая демагогия.
скиньте самое топовое что есть сегодня по к-теории, самое энтрилевельное, самое драйвовое, самое клёвое
по алгебраической, по топологической, по кк-теории, л-теории, е-теории, ...
Ты недостоин.
Вот сажу двачну, она хороша.
>Я с самого начала писал (), что вопрос в нише, а ты, фуфлыжник, начал пиздеть о якобы универсальности вольфрамоговна.
Основы для сигнал процессинга есть? Есть. Многим этого может хватить. Так с хуя ли не универсальна? Отсутствие йоба-библиотечки, которая решает твою любимую задачу, ничего не говорит об универсальности инструмента.
Ниши, разумеется, есть, но у математики ниша не только в символьных вычислениях. Ниша математики - в быстром прототипировании, и тут она делает всех мультипарадигменностью, а также широтой и интегрированностью всех своих инструментов. Реши задачу отсюда на матлабе , поржем вместе.
> с петушиным матлабовским синтаксисом
Не читал, но осуждаю. Не зная Матлаб, обсирать его. Поясни-ка, чем его синтаксис хуже пайтона, например? Да одна только реализация векторов в нампай -- уже кривое говно и костыли.
> то выяснилось, что в матлабе нужного мне типа хромосомы (и, соответственно, мутаций, скрещивания, и т д) нет в стандартных
Совсем охуели петухи всякие. Всё им на блюдечке подавай.
> В России у меня стоял матлаб с рутрекера.
Ну всё, прекрати. Я уже не могу ржать с тебя, дурака. Алсо > NLP Пфффф лол блеядь
> Нихуя математика не умеет
Пикрелейтед.
Вонючий лагающий кусок дерьма -- твой мозг, индюк тупой.
> Суть не в синтаксисе, а в том, что его долго и тяжело учить.
Даже не представляю, каким дегенератом надо быть, чтоб не осилить синтаксис Матлаба.
> В проприетарные пакеты всегда попадают только древние проверенные временем хуйни (читай - которые есть в учебниках) уже с десятком-другим open-source реализаций. То есть, практически нихуя не попадает. Как видишь, даже код из 80-х не всегда есть.
Эти маняфантазии.
> Те, кто работает в интернете - с обработкой языка, краулерами, бигдатой - любят питон.
Ссылку на статистику. Мы в наукаче, а не в б. Беспруфные кукареки идут на хуй.
> кококок трапическая никому ненужная НЁХ
> кокококо нигде не реалязована
> букбуккааааак в матиматике можна реализавать
> можна реализавать
Вся суть лисподолбаёбства.
> причем вводить и выводить формулы можно будет с использованием нотации из статьи: ⊕, ⊗. То есть можно будет писать A⊗B⊕C, а не вырвиглазное tropicalplus(tropicaltimes(A, B), C). Матлаб может такое? А питон? Где будет удобнее работать и получать результаты, и как скоро?
Пиздец, дегенерат. В мэплах и матемтаиках есть символический инпут для совсем не умеющих в программирование. Только подумай, какие проблемы с переносимостью могут быть у твоих хуй-пизда символов. ЯП были и ещё лет 1000 будут использовать текстовый инпут, потому что он прозрачен и не ведёт к конфузиям. Поэтому я даже предпочту мюбокс какому-нибудь мэплу, в котором хуй не знает, что там РЕАЛЬНО вводится. За Одни и толкьо make atomic нужно к стенке приставлять и расстреливать.
> A(:, 1) в матлабе
> A[[All, 1]].
> Одна хуйня
Ебаааааааааать. Просто пииииииздец.
> Но тот факт, что я не смог за разумное время взять и написать хотя бы что-то рабочее, когда мне это нужно было, много говорит ...
... о том, что ты дятел тупой криворукий, только и всего.
> самое клёвое - это питон + библиотеки
Главное - повторяй это почаще. А Матлабобоги будут попивать кофеёк в Kaffeepause, ухмяляясь над днищеёбами, которые им пытаются убого подражать.
>Основы для сигнал процессинга есть? Есть
МОЖНОЗДЕЛОТЬ
>Ну всё, прекрати. Я уже не могу ржать с тебя, дурака. Алсо > NLP Пфффф лол блеядь
Клоун.
huya ty
>Ко-ко-ко, нинужно, лисподебилы, ко-ко-ко
Все понятно
>Пиздец, дегенерат. В мэплах и матемтаиках есть символический инпут для совсем не умеющих в программирование. Только подумай, какие проблемы с переносимостью могут быть у твоих хуй-пизда символов. ЯП были и ещё лет 1000 будут использовать текстовый инпут, потому что он прозрачен и не ведёт к конфузиям. Поэтому я даже предпочту мюбокс какому-нибудь мэплу, в котором хуй не знает, что там РЕАЛЬНО вводится. За Одни и толкьо make atomic нужно к стенке приставлять и расстреливать.
Ко-ко-ко, я такова никагда нивидил, ита все ни будит работать, кудах-тах-тах. Символы вводятся Esc-последовательностью и биндятся к нужным операторам при подключении библиотеки, что уже было посчитано в 15и строчках кода. Символический инпут тут нахуй не нужен, и он неудобен в работе. Матлабодебил охуел от того, что можно не писать кодоговно вместо формул, и говно полезло у него из ушей, спешите видеть.
А ты не охуел тут с такими запросами приходить, чмошник?
> Символы вводятся Esc-последовательностью и биндятся к нужным операторам при подключении библиотеки
Всё. Убедил. Это ебать насколько удобнее ввода функции.
Если ты внимательно посмотришь на все его ответы, он пробежался по всем и написал возражение. Туповатый тролль, одним словом. Хотя ты еще тупее.
Матлабодебил не верит, что основную массу задач можно решить с нуля тем же количеством строк кода, что и для подключения йоба-библиотеки
http://habrahabr.ru/post/265961/
http://habrahabr.ru/post/266101/
пайтоноднище опять закукарекало
"Жертва пропаганды на хабре." как я и писал.
Ну и где использование экзотических символов, ввоядщихся Esc-последвательностью?
ну не знаю, мне норм, сам почитываю каждый день, ничерта не понимаю, зависимость есть, брат жив, но было интересно что анон читает и рекомендует, что вот ты, да, вот ты, что в к-теории котируешь
Ты не поверишь, записывать и читать формулу в инфиксной записи и без всяких сраных скобочек для аргументов функции гораздо удобнее, нежели наворачивать говна вида plus (1, minus (times (2, hui (pizda (dzhigurda (3, 4), 5), 6)), 7)). Хотя кому я объясняю..
Это к другому относилось, если ты не заметил.
Ну конечно, разложить вектор по базису не каждый дебил сможет, для этого либа специальная нужна.
ну, "к"
Это ты сам себе выдумал. Ты просил задачу - я тебе дал, напиши ту статью 1984 года с нуля. Ты ушел сосать хуи, а я заработал $2000. Вот и вся история.
> и без всяких сраных скобочек
> когда математика - уже лисподрочильня во-многом
В тех постах не используется символьная дрочильня, а норм программирование. Так в чём соль?
Суть в том, что если бы твоей чудо-либы не было, а был бы только набор стандартных функций, я бы на математике написал это быстрее. И я тебе дал статью 2015 года, и рассказал, как легко ее сделать, но ты ушел сосать хуи, даже не попытавшись заработать $2000.
> я бы, да кабы
Разговор уровня 5летнего дауна.
В том, что ты сравниваешь статический язык java, который неебически многословен даже по меркам статических языков, с интерпретируемым лиспом mathematica. При чем тут матлаб - не понятно. При чем тут "неиспользование готовых либ" - тоже, потому что я вижу, что он там как минимум вызывает kmeans.
Но ты так и не сделал это, 5и летний даун. А я могу показать тебе код в понедельник, когда приду на работу. Или могу сделать на бис сейчас, если ты дашь честное слово не кудахтать.
> сравниваешь статический язык java
Наркоман? Где я вообще яву приводил?
Что я не сделал? Ты меня путаешь с кем-то. Но вообще давай, валяй. 20 минут хватит тебе? Я молчу. Пиши код и выкладывай.
>В том, что ты сравниваешь статический язык java, который неебически многословен даже по меркам статических языков, с интерпретируемым лиспом mathematica.
Да без разницы, что там пару простых строк кода, что здесь - это я и хотел показать.
>При чем тут "неиспользование готовых либ" - тоже, потому что я вижу, что он там как минимум вызывает kmeans.
Тем, что метод kmeans зашит в стандартные средства языка, а не в либу?
>Да без разницы, что там пару простых строк кода, что здесь - это я и хотел показать.
Не, мальчик, ты погоди. "Наркоман? Где я вообще яву приводил?" - твои слова? Т.е. ты кинул ссылки даже не прочитав их? Я-то статью про яву читал, хмыкнул по поводу подбора инструмента и прошел мимо.
>Тем, что метод kmeans зашит в стандартные средства языка, а не в либу?
В матлабе тоже есть kmeans.
Не отвлекайте символикопетуха, он программу пишет.
Если бы не было чудо-либ, есть прекрасный язык Julia, который является матлабом на дрожжах. Только, прикинь, основное богатство языка - это код на нем. При появлении задачи, первым делом я смотрю где лучше всего инструменты. Чаще всего это матлаб, бывает питон, иногда - руби. Математика - никогда.
Набрал color deconvolution matlab и по первой ссылке нашел http://web.hku.hk/~ccsigma/color-deconv/color-deconv.html . Как видно, у чувака с хабра, пользующегося математикой, просто не тот алгоритм. Нет там никакой кластеризации. А правильный алгоритм занимает строчек 10 причем без лиспопердежа.
Что касается лиспопердежа, то
clusters =
ClusteringComponents[
original,
3,
Method -> "KMeans",
DistanceFunction -> CosineDistance
];
будет выглядить примерно как
[idx, C] = kmeans(original, 3, 'Distance', 'cosine'). Вот здесь видна разница между лиспом и языком программирования.
Короче, даже спорить не о чем. Матлаб - лучше всех. Всё остальное - только для специфических задача типа theorem proving.
Днищеёбы перебиваются убогими альтернативами. Чаще всего это пайтонопоедлки, типа нампай или саге.
Днищеёбы перебиваются убогими альтернативами. Чаще всего это пайтонопоедлки, типа нампай или саге.
Ну вот примерно так это выглядит. Какая-то еботня с паттернами, так бы было быстрее.
Все, вот так должно быть. Работает с точкой "бесконечность", как и требуется в статье. Тропически складывает, умножает возводит в степень числа, матрицы, использует нотацию из статьи. Сам код - верхняя часть, ниже - тесты.
Времени, конечно, ушло побольше, но час - все равно не так много.
> "Наркоман? Где я вообще яву приводил?" - твои слова?
Нет, не мои, откуда ты их взял?
И вообще причем тут ява, если я говорю о том, что ЗДЕЛОТЬ с имеющимися в математике инструментами не сложнее, чем найти и подключить либу. Похуй на яву в этом смысле.
>В матлабе тоже есть kmeans.
Здорово, я рад за матлаб.
>Как видно, у чувака с хабра, пользующегося математикой, просто не тот алгоритм. Нет там никакой кластеризации.
Потому что чувак выделял common цвета из картинки, а биолог хуярил их из очищенных образцов соединений.
>два куска кода
Здесь видна разница в говняности именования функций, ибо в математике функцией является общий алгоритм кластеризации, принимающий параметры, а в этой хуйне каждому методу завели по отдельной функции. Далее, вот эти штуки Method и DistanceFunction - это опции, передаваемые в функцию. В обычных говноязыках вместо этого опциональные аргументы, которые в лучшем случае подаются в виде f(x, option="A"), а в худшем им просто зарезервировано место в списке аргументов, как у тебя. То есть надо полезть в ман и посмотреть, куда эту свою 'cosine' вставить, чтобы заработало наконец. Ну и если записать ту дрисню на 7 строчек в одну, то будет выглядеть так же, как у тебя, так что что ты этим хотел показать - большой вопрос.
Ну и да, предлагается сравнить вот с этой процедурной дрисней на GAPе в 100 строк: https://github.com/mkotov/tropical/blob/master/tropical_algebra.g
Как это сравнивать, дятел, если этот перец сразу же начинает с >GenerateRandomMatrix и >GenerateRandomPolynomial
Не знаю, чо это за GAP, но он явно начинает с изобретения велосипеда
И, да, как я и сказал, твоя дристня не будет переносимой, пока не сбиндить notation. На нормальных ЯП ты берёшь функцию и применяешь её.
>И, да, как я и сказал, твоя дристня не будет переносимой, пока не сбиндить notation. На нормальных ЯП ты берёшь функцию и применяешь её.
Я вообще не понял, что ты этим хотел сказать. Модуль Notation идет вместе с самой математикой, так что у всех, у кого есть математика, он тоже есть. Далее, биндинг нотации к операторам выполняется вот теми строчками с желтеньким, которые и есть функции, собственно. Так что у всех это будет работать.
Тем не менее, если тебе это не нравится, можно ииспользовать стандартные операторы CirclePlus, CirclePower, и SuperScript, которые в математике специально выделены для использования пользователям, и альтернативная форма записи которых - как раз вот эти кружочки с плюсами. Т.е. при парсинге команды математика заменит кружочек с плюсом на CirclePlus и так далее. Я просто не стал так делать, т.к. у пользователя эти операторы уже могут быть переопределены. А перегрузка нотации эти операторы не затрагивает, и если пользователю хочется другие значки, то просто нужно изменить их в команде Notation.
>Как это сравнивать, дятел, если этот перец сразу же начинает с >GenerateRandomMatrix и >GenerateRandomPolynomial
>Не знаю, чо это за GAP, но он явно начинает с изобретения велосипеда
Поэтому я и не стал это реализовывать, хотя это точно так же пишется одной строчкой Table[RandomInteger[{xnin, xmax}], {i, 1, n}, {j, 1, n}]. Но даже если убрать у него то, что у меня не сделано, то все равно разница налицо. Вот хотя бы он перемножает матрицы, в форе умножая строчку на столбец, а я просто использую для этого функцию внутреннего произведения тензоров Inner.
>Здесь видна разница в говняности именования функций, ибо в математике функцией является общий алгоритм кластеризации, принимающий параметры, а в этой хуйне каждому методу завели по отдельной функции.
Самое забавное, что функция ga в матлабе так себя и ведет, но ты сказал ко-ко-ко-сложно и пошел писать собственный велосипед.
То есть на лицо синдром утенка - не важно, как удобно, главное, как в математике.
Потому что там нет таких параметров, которые можно передать, чтобы они меня устроили. А архитектурно сделано хорошо, я не спорю. Если бы у меня хромосомой был набор вещественных чисел, например, я бы делал в матлабе, потому что и мутация, скрещивание и отбор, скорее всего, были бы из списка "стандартных". Но - увы.
Чтоб ты понимал, задача у меня была расшифровать шифр Цезаря (где просто одна буква заменяется на другую по таблице, типа a -> к, б -> ф, и т д). И для этого я хотел в качестве хромосомы использовать таблицу замены букв, в качестве мутации - случайное изменение в этой таблице, в качестве скрещивания - некий хитровыдуманный алгоритм объединения двух кусков таблиц замены, а в фитнесс-функцию рассчитывать на основе соответствия словам из словаря русского языка. Вот что из этого можно было взять и юзать в матлабе, не реализуя самому? Да ничего.
x = ga(fitnessfcn,nvars,[],[],[],[],LB,UB,[],IntCon)
fitnessfcn - конечно, самому надо писать.
nvars - длина твоего вектора, т.е. 33 буквы.
LB - нижняя граница твоего вектора, то есть 1ones(1,33). UB - верхняя граница, т.е. 33ones(1,33).
IntCon - ключевой момент, число integer параметров оптимизации, 1:33 (т.е. все).
Далее, по хорошему, тебе нужно написать функцию генерации особей, чтобы не генерировались неуникальные перестановки. Но на практике это вряд ли потребуется (скорее всего будет даже хуже), проще добавить некий penalty при неуникальности.
Кроссовер и мутации тебе писать не нужно.
То есть по факту, на практике, для таких задач достаточно дефолтных настроек (для которых достаточно прочитать одну страничку в мануале). Тем функция ga в матлабе и ценна, если задача не сильно многомерная и нужно проверить принципиальную возможность оптимизации, можно запустить ga и проверить. Если работает - ковыряться уже с локальными методами.
>Далее, по хорошему, тебе нужно написать функцию генерации особей, чтобы не генерировались неуникальные перестановки. Но на практике это вряд ли потребуется (скорее всего будет даже хуже), проще добавить некий penalty при неуникальности.
1/33! - слишком маленький шанс, тут незачем над этим заморачиваться
>Кроссовер и мутации тебе писать не нужно.
Как это не нужно? Врети, все врети. Как там будет осуществляться кроссовер и мутации? Почему они будут такие, как я хочу? Есть ссылка на ман?
>1/33! - слишком маленький шанс, тут незачем над этим заморачиваться
Есть 2 целочисленных вектора из 33 чисел, ты много можешь придумать функций кроссовера и мутаций?
Не вектора, а перестановки, начнем с этого. Ну вообще довольно много, ведь я могу например, захотеть, чтобы при мутации одна буква перешла во-что то другое, чтобы две, чтобы три, чтобы некоторый цикл в перестановке провернулся на шаг, два цикла, могу просто захотеть изменить цикловую структуру перестановки - это все от задачи и фитнесс-функции будет зависеть, что лучше, т.е. это еще выяснить надо будет после проб и ошибок. То же самое со скрещиванием, в общем-то, я могу захотеть сохранить рандомные части от одной и второй хромосомы, а могу захотеть сохранить их общую часть и делить уже остальное, или сохранить отдельные замены букв, которые дают наибольший положительный вклад в фитнесс-функцию. Короче, тут все непросто.
>1/33! - слишком маленький шанс, тут незачем над этим заморачиваться
Блин. Я не об этом. А о том, что может быть табличка типа (a->б б->б в->б), т.е. разные буквы превращаются в одну и ту же букву. По идее, чтобы этого не было, ты можешь писать свои мутации и скрещивания. Но на практике может быть лучше не добавлять лишних ограничений, чтобы не создавать лишних поводов застревать в локальном минимуме. Я всегда просто добавляю лишние гладкие penalty в fitness-функцию.
Да, может быть, лучше не добавлять ограничений. Но в любом случае, я лишь хотел показать, что юзать стандартный инструмент для меня было болью, и я бы лучше питоновскую либу для ГА взял в любом случае. А что касается задачи, то на нее забили, ибо стало понятно, что самая большая задача здесь - составить хорошую годную фитнесс-функцию, что не очень-то просто сделать, тем более когда для ее вычисления нужно перекапывать словарь (т.е. это очень долго), ну или какую-то выжимку из него.
> В обычных говноязыках вместо этого опциональные аргументы, которые в лучшем случае подаются в виде f(x, option="A"), а в худшем им просто зарезервировано место в списке аргументов, как у тебя
Что ты этим хотел сказать вообще?
Я уже молчу про то, что перегружая эти символы, ты рискуешь засрать их использование в качестве тензорного произведения, скажем, или прямого плюса. Так что либо ты пишешь свою тропическую хуйню по-человечески, либо придумывай сам новые символы. Что в свою очередь будет весьма хуёвой и нечиательной идеей.
Что без чтения мануала ты будешь долго думать, надо ли писать kmeans(original, 3, 'Distance', 'cosine') или kmeans(original, 3, 'cosine', 'Distance') или еще как. А если метод принимает опций добрых два десятка, как, например, функция рисующая график (надо оси или не надо? шаг по оси сколько? легенды к осям надо или не надо? и какие? а к графикам легенды надо, если их несколько? и т д), то сразу становится видно, насколько подобная техника говена.
Уже сказал, что эти символы соответствуют пустым, зарезервированным для пользователя операторам. Так что изначально они не заняты. Если юзер их ничем не засрал, все будет работать. Если засрал, то у чего-то одного нотацию, очевидно, не удастся сохранить. И тогда придется для чего-то взять другие символы,и делается это просто заменой символа на другой в строчке Notation, или написание такой же строчки для нетропических функций. К оператору тем не менее всегда можно обратиться по полному имени, например TensorProduct. Мое решение такую возможность не портит. А писать всяко удобнее. В общем, все тут заебись, не надо придираться. Мы сейчас говорим о том, что ваши инструменты даже так не умеют, сколько с ними не ебись.
Мякотка еще, кстати, в том, что операторы имеют порядок прецедентности такой, какой математику надо, т.е. умножение с кружочком выполняется раньше сложения с кружочком, т.е. выражение A+BxC сразу работает как надо, не нужно засирать все скобками A+(BxC) и вообще ничего писать для этого. Над таким, я уверен, ни один язык не заморачивался.
Такое точно есть в хаскеле. 10 уровней приоритета.
Ну здорово, напиши это на хаскеле, благо два примера кода у тебя есть. Сравним.
>Тут работает равенство для любых i,j |aij|=|bij|, как я и преполагал. Надо опровергнуть это - либо попытаться доказать(мне в лом чёт ;).
Достаточно базис сделать позакрученней, пусть A = {{1,0},{0,1}}, B = {{1,0},{0,-1}} (Очевидно при этом, что A^2=B^2), C = {{1,2},{3,4}}
Тогда
CAC^-1 = A = {{1,0},{0,1}}
CBC^-1 = {{-5,2},{-12,5}}
Обе эти матрицы в квадрате дают Е.
Лень вспоминать наиболее строгие условия, но самые очевидные: когда частные производные существуют и непрерывны в окрестности точки, по которой дифференцируем (это тогда очевидным образом следует из теоремы Фубини и основной теоремы анализа).
Соответственно у функции (x^2+y^2)^1/2 частные производные в точке (0,0) не существуют, не говоря уже о непрерывности (достаточно взять сечение y=0 и увидеть, что это |x|, с дифференцируемостью которого всё понятно).
>по которой
Фикс: "в которой".
Фикс: "в которой".
>Соответственно у функции (x^2+y^2)^1/2 частные производные в точке (0,0) не существуют, не говоря уже о непрерывности (достаточно взять сечение y=0 и увидеть, что это |x|, с дифференцируемостью которого всё понятно).
Всмысле не существуют? Существуют там частные производные, просто в точке (0;0) там возникает деление на ноль и частные производные в ней имеют разрыв
Производная по х: х/(х^2 + у^2)^1/2
по у аналогичная
>просто в точке (0;0) там возникает деление на ноль
Это называется "не существует".
Сап, анон помоги решить задачу:
Функцию g определено как: каждому натуральному числу поставлено в соответствие остаток деление числа на 4. И соответственно доказать что g(x) = g(x-4) для любого натурального числа.
Функцию g определено как: каждому натуральному числу поставлено в соответствие остаток деление числа на 4. И соответственно доказать что g(x) = g(x-4) для любого натурального числа.
Кто-нибудь может посоветовать годную книгу по рядам Фурье, интересует общий случай, когда расклыдываются функции f:R->X, X - некоторое произвольное банахово пространство.
Возьмем любое число, например 123456.
Просуммируем его цифры
1+2+3+4+5+6 = 21; 2+1 = 3
Теперь возьмем 2 любых числа, которые в сумме дают 123456, например 78945 и 44502
Просуммируем их цифры
7+8+9+4+5 = 33
4+4+5+0+2 = 15
33+15 = 48; 4+8 = 12; 1+2 = 3
Складывать можно в любой последовательности, например
3+3 = 6; 1+5 = 6; 6+6 = 12; 1+2 = 3
В итоге все равно получим ту же сумму, что и у исходного числа 123456.
Почему так? Как можно доказать, что это должно быть именно так?
Просуммируем его цифры
1+2+3+4+5+6 = 21; 2+1 = 3
Теперь возьмем 2 любых числа, которые в сумме дают 123456, например 78945 и 44502
Просуммируем их цифры
7+8+9+4+5 = 33
4+4+5+0+2 = 15
33+15 = 48; 4+8 = 12; 1+2 = 3
Складывать можно в любой последовательности, например
3+3 = 6; 1+5 = 6; 6+6 = 12; 1+2 = 3
В итоге все равно получим ту же сумму, что и у исходного числа 123456.
Почему так? Как можно доказать, что это должно быть именно так?
>78945
78954
fix
но сути это не меняет.
Можно также брать сумму не 2-х чисел, а сколько угодно. Например
123456 = 569+9876+5964+54236+52811
5+6+9 = 20; 2+0 = 2
9+8+7+6 = 30; 3+0 = 3
5+9+6+4 = 24; 2+4 = 6
5+4+2+3+6 = 20; 2+0 = 2
5+2+8+1+1 = 17; 1+7 = 8
-------------------------
2+3+6+2+8 = 21; 1+2 = 3
там g(x+4)
Нет. Идея заменить символ тензорного произведения на свой, экзотический, продукт -- весьма плохая с точки зрения программирования. Это нарушает сам принцип перегрузки оператора. Есть общеизвестное правило: нельзя перегружать стандартную функцию стандартных операторов. Именно новый символ ты там, может, и введёшь, (типа какого-нибудь @ скажем) но читабельно и понимаемо это не будет. Поэтому лучший вариант -- это ExoticProduct[A, B].
Тащемта на Хассле можно использовать спецсимволы для функций.
И что ты пытался сделать?
http://www.for-stydents.ru/matematika/uchebniki/osnovy-matematicheskogo-analiza-v-2-h-tomah.html
Попробуй 2-й том стр. 371
ебаная сажа приклеилась
Смотри, собачка, какая хуйня. Первое вычисление A+B есть сумма, второе вычисление A+B - тензорное произведение. Угадай, почему так.
Это следует из того, что остаток от деления на 9 (как и на любое другое натуральное число) аддитивен, а так же из известного признака делимости на 9.
Да, следует не из этого, конечно, я упрлс. Достаточно просто воспользоваться теоремой о среднем а затем воспользоваться непрерывностью частных производных.
Из этого же следует, что достаточно существования частных производных в окрестности и их непрерывность в точке.
То есть подводя итог, частные производные у этой функции существуют, но имеют разрыв в (0,0), поэтому функция не дифференцируема? Иначе я не понимаю разницы между существованием частных производных и непрерывностью.
В точке (0,0) не существуют, конечно же.
>Иначе я не понимаю разницы между существованием частных производных и непрерывностью.
Это жаль, ну вот что такое производная функции f : R -> R в точке x0?
Ну мол x= 4a+b а дальше?
А x + 4 тогда чему равно?
И при чем тут остаток от деления на 9?
Аноны, хелп плиз
Пусть M2, M3, M5 – подмножества множества натуральных чисел, состоящие со-
ответственно из всех чисел, кратных 2, 3, 5. С помощью операций над множествами выразить через них множества всех чисел взаимно простых с 30
Пусть M2, M3, M5 – подмножества множества натуральных чисел, состоящие со-
ответственно из всех чисел, кратных 2, 3, 5. С помощью операций над множествами выразить через них множества всех чисел взаимно простых с 30
А почему остаток от деления именно на 9, а не на 5? И при чем тут признаки делимости? Где там деление?
погоди, в определении сказано, что необходимо и достаточно для того чтобы функция была дифференцируема в точке х0,у0, у нее должны существовать и быть НЕПРЕРЫВНЫМИ частные производные. Что в таком случае значит непрерывность? Я запутался.
>ну вот что такое производная функции f : R -> R в точке x0
предел отношения приращения функции к приращению аргумента
Непрерывность значит равенство пределов слева и справа значению функции.
Странно, у меня кнопка "ответить в тред" на некоторое время перестала работать.
Остаток от деления на 9 совпадает с результатом твоей процедуры "(натуральное, больше 0) число -> сумма цифр числа -> сумма суммы цифр числа -> ..." с точностью до того, что когда остаток 0, то результат твоей процедуры 9 (и наоборот). Почему это так можно понять, вспомнив признак делимости на 9.
>погоди, в определении сказано, что необходимо и достаточно для того чтобы функция была дифференцируема в точке х0,у0, у нее должны существовать и быть НЕПРЕРЫВНЫМИ частные производные. Что в таком случае значит непрерывность? Я запутался.
В моём утверждении (не определении) сказано только про "достаточно" это раз, и сказано кое-что более общее (что достаточно существования частных производных в окрестности и непрерывности в точке). Непрерывность значит то же, что и обычно: у нас df(x,y)/dx - это некоторая новая функция от x,y существующая (по условию утверждения) в окрестности точки, вот она как раз должна быть непрерывна по x,y в этой окрестности. То же самое и df(x,y)/dy касается.
>предел отношения приращения функции к приращению аргумента
Ну так подставь y = 0 в sqrt(x^2+y^2) и скажи, существует ли соответствующий предел в точке x0 = 0.
Остаток от деления на 9 совпадает с результатом твоей процедуры "(натуральное, больше 0) число -> сумма цифр числа -> сумма суммы цифр числа -> ..." с точностью до того, что когда остаток 0, то результат твоей процедуры 9 (и наоборот). Почему это так можно понять, вспомнив признак делимости на 9.
>погоди, в определении сказано, что необходимо и достаточно для того чтобы функция была дифференцируема в точке х0,у0, у нее должны существовать и быть НЕПРЕРЫВНЫМИ частные производные. Что в таком случае значит непрерывность? Я запутался.
В моём утверждении (не определении) сказано только про "достаточно" это раз, и сказано кое-что более общее (что достаточно существования частных производных в окрестности и непрерывности в точке). Непрерывность значит то же, что и обычно: у нас df(x,y)/dx - это некоторая новая функция от x,y существующая (по условию утверждения) в окрестности точки, вот она как раз должна быть непрерывна по x,y в этой окрестности. То же самое и df(x,y)/dy касается.
>предел отношения приращения функции к приращению аргумента
Ну так подставь y = 0 в sqrt(x^2+y^2) и скажи, существует ли соответствующий предел в точке x0 = 0.
>вот она как раз должна быть непрерывна по x,y в этой окрестности.
Точнее, функция должна быть непрерывна всего лишь в той точке (в которой исследуем на дифференцируемость).
Пересечь естественно.
Точнее, функция должна быть непрерывна всего лишь в той точке (в которой исследуем на дифференцируемость).
Пересечь естественно.
Матаны, спасайте. Как решить пикрелейтеды?
уверен, что решение какое-нибудь очевидное, но видимо не для меня, лол
уверен, что решение какое-нибудь очевидное, но видимо не для меня, лол
1) Формула Муавра
2) Представить в тригонометрической форме
С первым так вышло. Правильно или ка земля?
Нет.
А как правильно?
Не пересечь, а взять дополнение до их объединения
>тетрадь в узкую линейку
Третьеклашка что ли?
Пиздец, с кем сидим.
По делу есть что сказать?
Есть. С домашками - в /un.
Нет.
А нет, да, извиняюсь.
Я-то думал, что /sci/ солидное место, где каждый неопытный неофит может подойти к прошаренному профессору и задать глупый вопрос, при этом еще не быть посланным нахуй или в /un/, что еще хуже. Видимо все адекватные анончики не имеютт столько времени, чтобы сидеть на двачах, а сидят и доказывают теоремы, например. Пмздеу короче
Так вопросы: "подскажите, как можно интуитивно представить объект Х" или "подскажите, как используются в математике результаты теоремы Т" или "о чём, если популярно, написано в статье Z" немного отличаются от просьбы "проверьте мне домашку, а то мне не хватает мозгов забить этот пример в вольфрам и сверить ответы" не так ли?
Вынесите кстати в шапку нового треда ссылку на вольфрамальфу, ибо заебали.
Вольфрам часто хуйню выдает, отвечаю.
Я думаю, чаще вы хуйню пишете, чем он выдает.
Так я же не прошу решить все 20 своих задач. Только те, где он вероятнее всего выдает хуйню. Плюс раз уже такая хуйня, могли бы норм ответить и мы кто мы-то кстати? я здесь один съебались.
>раз уж это такая хуйня
Фикс
Ну чувак, сложно найти калькулятор с комплексными числами? http://ideone.com/892QjZ
Анон, я не могу понять комбинаторику. Что такое вообще бином Ньютона? Копал в интернете, но таки не смог понять :\
Кто может дать годной литературы? Или вот, например, объясните как я могу узнать сколько существует двузначных чисел в десятичной системе счисления, в которых нет одинаковых цифр?
Кто может дать годной литературы? Или вот, например, объясните как я могу узнать сколько существует двузначных чисел в десятичной системе счисления, в которых нет одинаковых цифр?
>Что такое вообще бином Ньютона? Копал в интернете, но таки не смог понять
На вики предельно ясно написано, что это.
>Или вот, например, объясните как я могу узнать сколько существует двузначных чисел в десятичной системе счисления, в которых нет одинаковых цифр?
Посчитать, сколько есть всего двузначных чисел, посчитать, сколько есть двузначных с одинаковыми цифрами, и вычесть из первого второе?
Да я могу тупо посчитать, но как сделать это с помощью комбинаторики? Например, надо будет узнать имеется пятизначных чисел в десятичной системе счисления, которые делятся на пять? Тоже тупо считать*?
Спасиб, анон.
Что за книга?
Предупреждаю, русский перевод ужасен, они даже в определении частичного порядка ошиблись.
А что по-твоему "не тупо считать"? Нам на лекциях по комбинаторике на мехмате лектор говорил, что труъ-подход - это строить взаимно-однозначное соответствие между интересующими тебя объектами и каким-то известным множеством, для которого количество элементов уже известно. Например, двузначные числа, у которых цифры совпадают, соответствуют натуральным числам от 1 до 9: отображение в числа: взять ту цифру, которая одинаковая, отображение обратно - взять число, состоящее из двух таких цифр. Не очень было понятно, в чем суть такого онанизма, но я подозреваю, что такой подход исключает всякое махание руками и прочее "очевидно, что" при доказательстве.
Ну или если вопрос был в том, как это посчитать без перебора всех чисел, то:
- Всего двузначных чисел 90, потому что есть 9 способов выбрать старший разряд (1,2, ..., 9), и 10 способов выбрать младший разряд (0, 1, ..., 9). Это надо перемножить, потому что из каждого способа выбрать старший разряд, и каждого способа выбрать младший разряд, можно составить число, причем числа, полученные таким образом, будут все разные.
- Двузначных чисел с одинаковыми цифрами 9, потому что старшую цифру мы можем выбрать 9ю способами (1, 2, ..., 9), а младшую мы не выбираем (1 способ), потому что она будет такая же, как старшая.
Вычитаем 90 - 9 и получаем 81, при этом мы все числа не перебирали. Это тебе надо было?
> Анон, я не могу понять комбинаторику. Что такое вообще бином Ньютона? Копал в интернете, но таки не смог понять :\
Ты так охуенно вопросы формулируешь. Вот что бы ты сам на свой вопрос ответил?
> Кто может дать годной литературы?
Тут надо просто задачи решать. Советую решать вот это
http://www.mccme.ru/free-books/yaschenko/v08book-08.pdf
Комбинаторика в третьем листке и еще где-то.
> объясните как я могу узнать сколько существует двузначных чисел в десятичной системе счисления, в которых нет одинаковых цифр?
Используй правило произведения: 9 x 9 = 81.
комбинаторика это наука о тупом счете. Вся ее основа это эмпирические наблюдения.
Не только.
Только. Все ее факты это эмпирика и ее следствия.Чтобы убедиться в этом достаточно почитать историю науки.
Про combinatiorial species мсье видимо ничего не слышал.
Пиздец наука просто. Я в свое время смотрел, что там. Во всех книжках из содержательного только комбинаторные интерпретации операций с экспонициальными производящими функциями. И Species тут нихуя не помогают даже неформально.
Статьитоже смотрел, ничего отличного от припудренной стандартной комбинаторики (кстати, не считаю ее чем-то плохим) не заметил.
Спасибо, умный анон. Про аддитивность остатков как-то не подумал, хотя чисто интуитивно сам тоже почему-то сначала начал смотреть признаки делимости, но в конце концов не понял куда их можно применать.
теория множеств это наука деланья вид, что решение задачи есть без решения самой задачи. Вся ее основа это маняфантазии верунов.
>решение задачи
Адепты второй культуры считают решением задач не решение задач, которые инженер поручил им решить, а решение каких-то ебанутых примерчиков на смекалочку, сгенерированных левой пяткой стариков-решальщиков. Спасибо, но жрите вашу смекалочку сами.
Понятно, манька не знает, что наиболее красивые примерчики на смекалочку берутся из нормальных математических результатов упрощением (подстановкой параметра, переписыванием в координатах и т.д.). Гугли неравенство Коши-Буняковского, а потом его же, но в координатной записи. Первое - результат, второе - задачка для олипмиадника.
Алсо, ты думаешь, что если человек может решить специально сгенерированную херню посложнее, то он не сможет решить инженерную задачу?
Во-во, попёрла вторая культура. Зачем изучать нормальные математические результаты? Мы лучше заменим, переставим, запишем в координатах и получим примерчик на смекалочку, ёпт.
Инженерные задачки более-менее осмысленны. Бессмысленность высосанных из пальца примерчиков очевидна. Разумный человек не занимается трудом, бессмысленность которого ему очевидна. Поэтому либо для второкультурщиков решение примерчиков не является трудом, либо второкультурщики не разумны. В первом случае второкультурщики поехавшие, во втором - дебилы.
>Инженерные задачки более-менее осмысленны.
>Разумный человек не занимается трудом, бессмысленность которого ему очевидна.
Лол, инженерное быдло рассказывает за вторую культуру.
Что ты вообще делаешь в мат.треде, клоун?
Иди примерчики решай, быдло. Верно ли, что существует только семь вещественных чисел a,b,c таких, что a/7+7b + c^7 = 7? Верно ли, что если в школе учатся ровно двадцать детей и у любых двух из них есть общий дед, то у одного из дедов в школе учатся не менее четырнадцати внуков и внучек? В плоскости отмечена 101 точка, не все из них лежат на одной прямой, через каждые две точки проведена красная прямая, верно ли что на плоскости существует точка, через которую проходит не меньше одиннадцати красных прямых? Используй смекалочку.
Сука в голос
Смачный бубалех недалекого "первокультурщика". Впрочем, и так очевидно, что только интеллектуально опущенному петуху нужно в любом разговоре с нормальными людьми подчеркивать, что ОН ТУТ САМЫЙ ГЛАВНЫЙ.
1. Неверно, одно уравнение, три неизвестных, бесконечно много вещ. решений.
2. Верно, т.к. если у любых двух общий дед, то у всех общий дед
3. Верно, т.к. если через любые две точки проходит красная прямая, то через каждую точку проходит 100 красных прямых,
Проблемы, дауненок?
->
Лол, он правда начал это решать.
К тому же не поняв условие.
Примерчики и задачи на смекалочку никогда не были зашкваром для математиков - все с них начинали; инженерные задачи не являются приоритетными у математиков, более того, большая часть современный математики с точки зрения практичности будет бессмысленной для незаинтересованного обывателя (разумного человека, если хочешь). Приоритетность задач диктуется нуждами текущего положения вещей в МАТЕМАТИКЕ, а не инженерии. Любой матфаковец это знает и понимает, но инженеро-быдлу конечно не осилить.
Возражу. Примерчики и задачи на смекалку были зашкваром ещё у древних греков. Инженерные задачи чрезвычайно интересны для математиков, поэтому каждая нуждающаяся в математике инженерная задача решена, часто многими разными способами. У инженеров очень редко возникают новые, оригинальные задачи, и каждая из них мгновенно привлекает к себе внимание. Например, возникшая у инженеров задача распознавания образов породила свою собственную науку.
Дело в том, что придумать задачу, которая решается элементарными методами, но при этом не в лоб - не настолько просто, как ты думаешь. А сделать при этом задачу с красивым условием и удивительным решением , не спиздив ее из глубокой науки - искусство.
В чем для инженера польза от задачи определения разрешимости уравнения в радикалах, например?
Я нигде не утверждал, что математики занимаются решением только инженерных задачек, или что математика есть обслуживающая дисциплина для техники. Я утверждал, что инженерные задачи интересны математикам, и каждая из них решена.
> если у любых двух общий дед, то у всех общий дед
Неверно, так как у одного человека может быть больше одного деда.
Тут анон с десяток тредов назад кидал статистику, лень искать, но суть в том, что большинство известных математиков были олимпиадниками в свое время, и занимали призовые места - решали задачи на смекалочку, и не считали это зашкваром.
>Инженерные задачи чрезвычайно интересны для математиков
Для некоторых математиков, уверен, для меньшей части из математиков. Большинству плевать на нужды инженерии.
Тогда к какому классу задач относится эта задача? Примерчик на смекалочку? А ВТФ?
На самом деле, пиздеж о бессмысленности некоторых задач, ответный вскукарек о их важности, классификация задач и математиков - всё это всё тоже мерение пиписек отчаяных короткостволов. Дескать у какой категории людей есть претензия на большую интеллектуальность.
Математиков терпят только потому, что их предшественники часто доказывали, что рожали матаппарат задолго до подходящей инженерной задачи. Вот на этом невысказанном предположении и держится весь хрупкий механизм нашего молодого народовластия.
Именно так. Ты думаешь, я пытаюсь доказать, что решать задачки - важнее, чем развивать теорию? Я пытаюсь доказать, что это все одинаково важно, потому что это все математика. А разделить ее на части, чтобы ту, которой занимаешься сам, назвать илитной, а ту, которой не занимаешься, назвать нинужной - удел ущербных петухов, которые не могут в обе эти вещи.
Дартаньян Сергеевич, залогиньтесь.
Сап, матанч (лол), посоветуй книжек по комбинаторике и графам для программеров. Чтобы задачки по спортивному программированию решать.
"Дискретная математика для программиста".
То, что нужно, спасибо.
Так, а теперь быстро мне пояснили, почему предел:
ln(y)/x^2, (x,y)->бесконечность
не существует.
альсо, Вольфрам пиздит или не так понимает пример, поэтому на него не ссылайтесь
ln(y)/x^2, (x,y)->бесконечность
не существует.
альсо, Вольфрам пиздит или не так понимает пример, поэтому на него не ссылайтесь
Это ты не понимаешь, что пишет вольфрам.
http://www.wolframalpha.com/widgets/view.jsp?id=2958433016861a528d6221f5ac88eefd
Если x, y принимают вещественные значения, то, предела нет, потому что пределы по разным направлениям будут разные. Если - вещественные, то 0. Пусть v = (v1, v2) - вектор, задающий выбранное направление, тогда предел по этому направлению - это предел по t, где вместо x ставим t v1, а вместо y - t v2. Какой предел у ln(t)/t^2 на бесконечности? А у ln(2t)/t^2? А у ln(t)/(2t)^2? А у ln(t v1)/(t v2)^2 для произвольных ненулевых v1, v2? Везде 0.
Виктор Олегович, рано вам ещё о Науке рассуждать, вот что вы в предисловии "Цукербринов" за хуйню написали? Без слёз же читать невозможно. А ещё и купил зачем-то, нестыдно вот вам?
Вестимо потому что по путям (e^t, t^(1/2)) и (t,t) предел разный. Выше кун не шарит, то что по любому лучу предел 0, ещё не гарантирует предела 0 по базе (n,m) \to \infty
>нестыдно
не стыдно
>по базе (n,m) \to \infty
(x,y) \to \infty
я пспать короч.
не стыдно
>по базе (n,m) \to \infty
(x,y) \to \infty
я пспать короч.
Лол, какую же ты хуйню сказал в 2 и 3.
По модулю очевидных предположений, что у каждого ученика школы ровно один дед, и что "каждые две точки" - это не совсем каждые а каждые две из набора именно тех фиксированных 101 точки из условия задачи, а также того, что эти задачи вообще были шуткой и решать их было не надо, вроде как у него всё верно. А что не так?
окей, пацаны, а я могу решать эту йобу путем обычной подстановки константы сначала в икс, а затем и в игрек? устремляю икс к константе, а игрек к бесконечности, получаю бесконечность
устремляю у к константе, х к бесконечности, получаю 0, таким образом предел не существует
nyet.
Под символом (x,y) -> infty обычно понимается база, равная произведению баз x -> infty, y -> infty, а когда ты подставляешь константу, то это совсем никак не x -> infty.
Аноны, посоветуйте годный учебник по вариационному исчислению и интегральным уравнениям. Можно на английском.
Алсо, скачал мгушный курс лекций по интурам. Обязательно учебник по математике наполнять определениями на 90%? Я понимаю, что это строгость, и ничего против такого изложения не имею. Но иначе нельзя? Ладно я как физик знаком с операторным пространством, мне понятно зачем этот огород городить. А математики?
Алсо, скачал мгушный курс лекций по интурам. Обязательно учебник по математике наполнять определениями на 90%? Я понимаю, что это строгость, и ничего против такого изложения не имею. Но иначе нельзя? Ладно я как физик знаком с операторным пространством, мне понятно зачем этот огород городить. А математики?
Дебил-погромист вкатился. Что значит при (x, y) -> бесконечность? Я чет не могу придумать определение. Я знаю, что такое x -> бесконечность (для всех x больше какого-то M), знаю, что такое (x, y) -> (x_0, y_0) (для всех (x, y) в эпсилон-шаре с центром в (x_0, y_0)). А че значит (x, y) -> (бесконечность, бесконечность)?
Тащемта, проблем тут нет. Это значит для любого eps, существуют M1, M2 для которых при x > M1 && y > M2 или каноничнее для пробной точки A существует радиус сферы M вокруг нуля, за пределами которой соблюдается условие A(eps)
Вообще у меня есть объяснение, почему предел в (беск, беск) не существует. Выберем сколь угодно большое x и любое eps > 0. Тогда найдется такое y, что значение твоей функции в точке (x, y) будет больше eps.
это называется предел равен бесконечности(значение м.б. больше любого конечного числа).
вот это знаток всё правильно объяснил - в случае многомерности предел должен существовать и давать одинаковый результат по любой траектории "схождения" к точке, чего не происходит в данном случае.
Самое интересное, что ты назвал два неэквивалентных определения.
Вообще так никто не пишет, обычно пишут либо
x -> \infty, y -> \infty (две строчки под знаком lim), либо как-то типа v -> \infty предварительно оговаривая, что v = (x,y).
В первом случае определение примерно такое: lim(x->\infty, y->\infty) f(x,y) = A, если для любого eps, существуют такие M,N>0, что |x|>M, |y|>N следует, что |f(x,y) - A| < eps
В втором случае определение примерно такое:
lim(v->\infty) f(v.x,v.y) = A, если для любого eps, существует такое M>0, что из x^2+y^2>M^2 следует |f(v.x,v.y) - A| < eps.
Вообще - это две частные конструкции так называемого "предела по базе", можно сказать, что базу в первом случае образуют все множества вида B_{N,M} = {x,y \in R: |x|>M, |y|>N} (N,M \in R_+)
А во втором случае базу образуют дополнения до всех ограниченных множеств.
Я кстати сам погромист, однако конструкцию предела по базе мне не составило расшарить никакого труда.
Поясните за книжку Арнольда "Обыкновенные дифференциальные уравнения", какие там prerequisites? Я знаю самые основы топологии (в Рудине было), всякие интегралы под картофанчик считать умею. Мне казалось, этого должно быть достаточно, а там на первой странице
> Процесс называется дифференцируемым, если его фазовое пространство имеет структуру гладкого многообразия
Полез в википедию читать, что такое гладкое многообразие, и у меня создалось впечатления, что мне еще дохуя чего надо знать, чтобы читать эту книгу. Так вот, есть 3 варианта.
а) Читать Арнольда и пропускать то, что непонятно.
б) Пока оставить его и почитать про анализ на многообразиях (это же так называется, да?)
в) Выбрать другую книгу по ODE. Хотелось бы, чтоб стиль был как у Рудина, но я такого не нашел.
Че делать, посаны?
> Процесс называется дифференцируемым, если его фазовое пространство имеет структуру гладкого многообразия
Полез в википедию читать, что такое гладкое многообразие, и у меня создалось впечатления, что мне еще дохуя чего надо знать, чтобы читать эту книгу. Так вот, есть 3 варианта.
а) Читать Арнольда и пропускать то, что непонятно.
б) Пока оставить его и почитать про анализ на многообразиях (это же так называется, да?)
в) Выбрать другую книгу по ODE. Хотелось бы, чтоб стиль был как у Рудина, но я такого не нашел.
Че делать, посаны?
Если тебе нужен прикладной аспект - клади хуй на Арнольда, изучай ДУ "для инженеров". Либо в аспекте численных методов. Все решаемые аналитические ДУ(или почти все) - решены, выписаны в явном виде, их "режимы" изучены. Теорию линейных ДУ можно изучить и будучи "инженером головного мозга". Дерзай.
Прочитай двухтомник Зорича.
А чем вам инженеры не нравятся? То, что они лезут со своим НЕПРИКОКОКЛАДНОЕ - НИНУЖНО?
Мне нужен прикладной аспект, но при этом я хочу, чтобы были доказательства и все такое. Потому что если что-то ублюдочно в эстетическом плане, я не смогу заставить себя этим заниматься.
Инженеры нравятся. Недоинженеры, которые ничего на самом деле не делают, а только в стодесятый раз рассчитывают сферическую гайку в вакууме и выдают это за важную науку, - не нравятся.
в "инженерных" книгах как правило приводятся важные доказательства и технические приёмы решения. Некоторые доказательства(вроде существования и единственности решения) опускаются по "понятным" причинам(сложные либо задействуют матан) - можешь смотреть их отдельно. Конкретную книгу посоветовать не могу - сам как-то планировал укрепить знания в ДУ, но так толком и не проштудировал - с древних времен на харде валяются книжки Понтрягина(думаю, всем знакомая фамилия), Филипова, Самойленко, лекции некоего Пунтуса из какого-то универа(там краткая выжимка). Понтрягин показался суховатым, но по делу, Филипов - интересным и мотивирующим со всякими занятными байками по ходу дела.
>равная произведению баз
но ведь бесконечность на константу это та же бесконечность, вай нот?
давай по русски, что за esp?
Я думаю что человек, прочитавший Рудина, знает различие между инженерными и неинженерными книгами.
Даже не знаю как на это и ответить. Во-первых это верно лишь при некоторых интерпретациях значка "infty", а при других неверно, во-вторых, при чём тут это?
epsilon - эпсилон. Дивана в тебе предчувствую я
>лишь при некоторых интерпретациях
Очевидно, он имеет в виду расширенную вещественную прямую. На это указывает разделение величин на переменные и константы в его мышлении. Такая терминология традиционна для курсов XIX века (используется, например, у Фихтенгольца), а для XIX века самым естественным пониманием ∞ является осмысление через расширенную прямую. Нет смысла усложнять.
Ну очевидно так очевидно, второй вопрос всё равно в силе.
Кстати, я на твоём месте всегда выбираю вариант 1, на крайний случай к материалу можно будет вернутся и чуть позже, но понимание его всё равно будет глубже, чем если читаешь в первый раз. Так что я бы сделал так, читал Арнольда и параллельно где-то попробовал бы вычитать главу по гладким структурам на многообразиях (в том же Зориче, Львовском). По поводу книг, помимо Арнольда ещё хвалят: Yulij Ilyashenko and Sergei Yakovenko. Lectures on analytic differential equations.
Скопенков норм?
да я и так диван гуманитарный, пришел спросить советов мудрых
я все таки не понимаю тогда, как аналитически доказать что предела нет? а именно аналитическое доказательство от меня будет требовать преподаватель на экзамене
Аналитическое доказательство такое: по путям (e^t,t^1/2) и (t,t), t>0 предел разный, а если предел x->infty y->infty существует, то он должен существовать и быть одним и тем же и по любому пути, компоненты которого стремятся к бесконечности. Противоречие.
>Вестимо потому что по путям (e^t, t^(1/2)) и (t,t) предел разный.
Уважаемый магистр клуба ответил же - подставляй x, y равными выражениям в скобках(это будет выбором траектории) - считай пределы при t->inf, показывай что они разные. Ч.т.д.
ананас, только не психуй, я гуманитарий
что за пути e^t? мы заменяем икс и и игрек на одну и ту же переменную, т.к траекторию? давай вообще как для самых маленьких по частям
так, ну хорошо, получается что при
ln(e^t)/t^1/2, t-> бесконечность, предел равен бесконечности
при ln(t)/t, t->бесконечность, предел равен нулю
Это правильно? Если да, то почему поочередно нельзя устремлять икс к контанте а потом и игрек, ведь доказательство получится идентичным?
Альсо, почему нельзя заменять игрек на какую нибудь траекторию х? потому что это независимые друг от друга переменные?
А потому что последовательное взятие пределов - это тоже траектория, похожая на прямоугольный уголок. То, что предел вычисляется таким образом - значит он существует при такой траектории. При других траекториях он может быть другим/не существовать. Про y=f(x) - так тоже можно задавать траекторию, но параметрическое задание(через t) зачастую удобнее т.к. траектория может не являться функцией от x(много значений с одним и тем же x).
>ln(e^t)/t^1/2, t-> бесконечность, предел равен бесконечности
>при ln(t)/t, t->бесконечность, предел равен нулю
С учётом того, что в знаменателе был x^2 и искомый предел должен получится был 1, вроде как правильно.
>Если да, то почему поочередно нельзя устремлять икс к контанте а потом и игрек, ведь доказательство получится идентичным?
Ну давай попробуем совсем образно, представь график f(x,y) - это, в общем случае, какой-то рельеф, и представь что ты стоишь в точке (1,1, f(1,1)) этого рельефа. И вот тебя спрашивают "если ты очень долго будешь бежать по направлению правого верхнего или левого верхнего угла координатной плоскости, то какая, примерно, будет высота"? И ты такой типа отвечаешь: "может быть и такая, и эдакая, потому что если я буду бежать строго вправо (по пути (1,t)) то высота будет всё ближе приближаться к 0, а если буду бежать строго вверх (по пути (t,1)) то высота будет всё возрастать и возрастать". Но разве тебя об этом спрашивали? Просили бежать на северо-восток, а ты бежишь сначала на север, потом на восток, а потом делаешь из этого какие-то выводы.
Но тут вообще есть тонкий момент, у тебя было написано (x,y) \to \infty или x \to \infty, y \to \infty? В первом случае твоё рассуждение верно (так как тебя спрашивают что будет, если бежать как можно дальше от той точки, где ты стоишь), а во-втором - нет (однако в любом из этих случаев ответ один и тот же).
>Альсо, почему нельзя заменять игрек на какую нибудь траекторию х? потому что это независимые друг от друга переменные?
Потому что ты вычислишь при этом не требуемый предел, а нечто иное (предел при стремлении по траектории).
(x,y)->бесконечность, а не x-> inf, y-> inf
Спасибо, анон, может быть я даже сдам матан.
А, ну тогда ты про подстановку констант всё правильно говорил, это у меня что-то переклинило. В сентябре что-то сдавать? Пересдача что ли? Удачи, в любом случае.
Пересдача, да. Еще и по дискретной математике есть, может быть я еще сюда пару задачек залью. Спасибо.
Анон, а вот еще такой вопрос, а как доказать существование предела?
аналогичным образом с контантами? Это пойдет за доказательство?
вот например предел (x^2+y^2)/(x+y), (x,y)->0
ну в данном пределе константы не требуются, я просто посчитал предел при х, приравняв игрек к нулю и наоборот, в обоих случаях получил ноль. ну а вообще в других случаях?
>ну в данном пределе константы не требуются, я просто посчитал предел при х, приравняв игрек к нулю и наоборот, в обоих случаях получил ноль.
В обоих случаях получил неправильно. Но даже если бы это было правильно, то этим ты не узнал ровно ничего. Опять же та же самая аналогия с рельефом, вот спрашивают тебя, какая будет примерно высота, если отойти от точки (0,0) очень длаеко? И ты такой отвечаешь: будет примерно 0, сходил на север там 0, сходил на восток, там тоже 0, поэтому если идти по любому пути, то тоже будет 0. Разве это логично?
Конкретно в твоём случае - перейти к полярным координатам и заметить, что получается выражение r^2/( r(ограниченная функция) ) которое естественно равно понятно чему.
Я дурак, прочитал как (x,y) -> inf. 0 конечно, но в остальном все объяснения в силе (в том числе и способ решения).
хм, без полярных никак?
просто препод ничего против них не имеет, но он как то по другому все это доказывал
ну сам предел существует и равен нулю, ведь так?
И кстати, а почему мы имеем право перейти к полярным координатам? Идем по всем траекториям? Но почему в прошлом пределе нельзя было так сделать?
>ну сам предел существует и равен нулю, ведь так?
Так.
>хм, без полярных никак?
>просто препод ничего против них не имеет, но он как то по другому все это доказывал
Можно и по определению но, как говорит Вербцикий: "математика - это искусство превращать формулы в слова, а не наоборот". Ну вот окей, пусть нам задан eps>0 какое delta>0 нам нужно взять, чтобы из x^2+y^2<delta^2 следовало |(x^2+y^2)/(x+y)| < eps?
>И кстати, а почему мы имеем право перейти к полярным координатам?
Ну, если совсем строго, то есть некоторая теорема о композиции пределов, которая это делать позволяет. Ну а если нестрого: то почему бы и не должны мочь? Какая разница (для вычисления предела), парой каких чисел мы представляем точку?
>Идем по всем траекториям?
Не понял о чём ты.
>Но почему в прошлом пределе нельзя было так сделать?
Как говорил один хороший человек: "Знаешь как делают модельки корабликов в бутылках? Засовывают в бутылку детальки, заливают туда клей и трясут, получаются разные странные штуки, иногда корабли.", вот так и тут, тут переход к полярным координатам позволяет что-то увидеть, а там не позволял. Научиться "чувствовать" какие приёмы могут приводить к решению каких задач можно только много этих задач прорешавши.
Так.
>хм, без полярных никак?
>просто препод ничего против них не имеет, но он как то по другому все это доказывал
Можно и по определению но, как говорит Вербцикий: "математика - это искусство превращать формулы в слова, а не наоборот". Ну вот окей, пусть нам задан eps>0 какое delta>0 нам нужно взять, чтобы из x^2+y^2<delta^2 следовало |(x^2+y^2)/(x+y)| < eps?
>И кстати, а почему мы имеем право перейти к полярным координатам?
Ну, если совсем строго, то есть некоторая теорема о композиции пределов, которая это делать позволяет. Ну а если нестрого: то почему бы и не должны мочь? Какая разница (для вычисления предела), парой каких чисел мы представляем точку?
>Идем по всем траекториям?
Не понял о чём ты.
>Но почему в прошлом пределе нельзя было так сделать?
Как говорил один хороший человек: "Знаешь как делают модельки корабликов в бутылках? Засовывают в бутылку детальки, заливают туда клей и трясут, получаются разные странные штуки, иногда корабли.", вот так и тут, тут переход к полярным координатам позволяет что-то увидеть, а там не позволял. Научиться "чувствовать" какие приёмы могут приводить к решению каких задач можно только много этих задач прорешавши.
Окей, в примере если решать через полярные мы получили
r/(cos(a)+sin(a)), но ведь в случае если угол альфа равен pi*n-pi/4, у нас возникнет неопределённость 0/0, как быть?
>по всем траекториям
Я имею в виду что мы приближаемся к 0 по всем прямым, параболам и т.д
блин я уже запутался, или мы приближаться так можем только если x->0,y->0
>r/(cos(a)+sin(a)), но ведь в случае если угол альфа равен pi*n-pi/4, у нас возникнет неопределённость 0/0, как быть?
А как быть в случае (x^2+y^2)/(x+y) в случае, когда x=-y? А никак не быть, когда говорят о пределе функции в точке то, чаще всего, подразумевают, что точка "стремится" по области определения функции. Мне тоже кажется, что такие штуки на первом курсе нужно прописывать в задачах явно типа как-нибудь $(x,y) -> 0, x+y!=0$, но щито поделать, не все разделяют мою точку зрения.
>Я имею в виду что мы приближаемся к 0 по всем прямым, параболам и т.д
Так мы и приближаемся к 0 по всем прямым параболам и т.д. Точнее так, то, что lim [(x,y) -> (0,0)] f(x,y) = A эквивалентно тому, что предел по любой непрерывной траектории, оканчивающихся в нуле, существует и от траектории не зависит.
>блин я уже запутался, или мы приближаться так можем только если x->0,y->0
Пределы (x,y) -> (0,0) и x->0, y->0 это одно и то же (в отличии от случая, когда вместо 0 стоит inf).
А как быть в случае (x^2+y^2)/(x+y) в случае, когда x=-y? А никак не быть, когда говорят о пределе функции в точке то, чаще всего, подразумевают, что точка "стремится" по области определения функции. Мне тоже кажется, что такие штуки на первом курсе нужно прописывать в задачах явно типа как-нибудь $(x,y) -> 0, x+y!=0$, но щито поделать, не все разделяют мою точку зрения.
>Я имею в виду что мы приближаемся к 0 по всем прямым, параболам и т.д
Так мы и приближаемся к 0 по всем прямым параболам и т.д. Точнее так, то, что lim [(x,y) -> (0,0)] f(x,y) = A эквивалентно тому, что предел по любой непрерывной траектории, оканчивающихся в нуле, существует и от траектории не зависит.
>блин я уже запутался, или мы приближаться так можем только если x->0,y->0
Пределы (x,y) -> (0,0) и x->0, y->0 это одно и то же (в отличии от случая, когда вместо 0 стоит inf).
>и от траектории не зависит.
И равен А.
И равен А.
Кажется, в древности не знали математической индукции,
и как способ доказательства она появилась, не раньше17 века.
Сейчас индукция (если утверждение верно для 1, и из его верности для N следует верность для N+1, то утверждение верно для всех натуральных чисел) рассматривается как одно из логических правил вывода (я не специалист по логике и могу напутать с терминологией).
Предположим, что мы запретим это правило и окажемся на месте древних математиков.
Что тогда мы сможем доказать и какие теории построить?
и как способ доказательства она появилась, не раньше17 века.
Сейчас индукция (если утверждение верно для 1, и из его верности для N следует верность для N+1, то утверждение верно для всех натуральных чисел) рассматривается как одно из логических правил вывода (я не специалист по логике и могу напутать с терминологией).
Предположим, что мы запретим это правило и окажемся на месте древних математиков.
Что тогда мы сможем доказать и какие теории построить?
>и как способ доказательства она появилась, не раньше17 века.
https://ru.wikipedia.org/wiki/Метод_исчерпывания
Ой, я всё наврал кажись, предел не существует. Если alpha стремить быстро к pi/2+pi/4, а r стремить медленно к 0, то получить можем что угодно, извиняюсь, я тупой. 3:
Так-с, значит есть два алгоритма, если все стремится к inf, ебашим через константу, если предел к нулю, то лучше через полярные. Эх, почитал бы теорию, но в учебниках мало что понятно.
Кстати, у меня есть еще один вопрос: как вычислять уравнение касательной к линии равного уровня, проходящей через точку (x0,y0)
Гугол молчит, в учебниках ничего
>Так-с, значит есть два алгоритма, если все стремится к inf, ебашим через константу, если предел к нулю, то лучше через полярные.
Тогда уж "если предел не существует, то через константу, а если нет, то через полярные".
>Кстати, у меня есть еще один вопрос: как вычислять уравнение касательной к линии равного уровня, проходящей через точку (x0,y0)
Это известная "теорема о неявной функции". Если f(x,y) = C и df(x,y)/dy != 0, то существует функция Y(x) такая, что в некоторой окрестности точки x0,y0 справедливо тождество f(x,Y(x)) = C отсюда справедливо f'x + f'y y'x = 0, а отсюда y'x = -f'x/f'y
тобишь уравнение касательной
y = f(x0) - (x-x0) f'x/f'y
f'x и f'y - частные производные.
Да, и с тем примером про (x^2+y^2)/(x+y) я бы советовал таки придумать путь, по которому предел не 0.
>если предел не существует
боюсь, просто логически до этого дойти я не смогу, мне надо аналитически решать разными способами
>df(x,y)/dy != 0
Частная производная по игрек в точке? или просто условие что игрек не константа?
хм, спасибо, анон, пойду гуглить теорему
Ты действительно прогер, а не математик? У меня бы из головы все вылетело, даже если бы я хорошо знал матан.
>Частная производная по игрек в точке? или просто условие что игрек не константа?
Нет, просто условие, что касательная не вертикальная.
>Ты действительно прогер, а не математик? У меня бы из головы все вылетело, даже если бы я хорошо знал матан.
Ну, если коротко, то я ещё студент и специальность у меня называется "прикладная математика", но преподают её так, что она не имеет ничего общего ни с математикой, ни с программированием, ни с прикладной математикой, что печально, посему на парах я бываю редка. Подрабатываю фрилансом на upwork'e, задачи не шибко интеллектуальные, но на жизнь хватает, по вечерам читаю книжечки по математике, ибо интересно. Таки вот дела.
А путь по которому предел не ноль у (x^2+y^2)/(x+y) ты всё-таки придумай.
Нет, просто условие, что касательная не вертикальная.
>Ты действительно прогер, а не математик? У меня бы из головы все вылетело, даже если бы я хорошо знал матан.
Ну, если коротко, то я ещё студент и специальность у меня называется "прикладная математика", но преподают её так, что она не имеет ничего общего ни с математикой, ни с программированием, ни с прикладной математикой, что печально, посему на парах я бываю редка. Подрабатываю фрилансом на upwork'e, задачи не шибко интеллектуальные, но на жизнь хватает, по вечерам читаю книжечки по математике, ибо интересно. Таки вот дела.
А путь по которому предел не ноль у (x^2+y^2)/(x+y) ты всё-таки придумай.
Хм, однако. Так вот, насчет предела, сходу как то придумать не выходит, в процессе решения лопиталем всегда получается ноль. Тьфу ты. ну может какие нибудь тригонометрические траектории подойдут
Ну так да, в полярных координатах радиус стремить медленно, а угол к 3pi/4 стремить быстро.
Правило Лопиталя, в том виде, в котором его знаю я формулируется только для функций одно переменной. Может многомерные обобщения и есть но я бы не стал просто так брать и дифференцировать (по какой переменной, кстати)?
ну да, ты прав, но мы же как бы заменяем игрек на траекторию по иксу и получаем предел по одной переменной
Вроде я нашел такую траекторию. cos(x)
там предел при подстановке сразу дает 1
>ну да, ты прав, но мы же как бы заменяем игрек на траекторию по иксу и получаем предел по одной переменной
На какую траекторию?
>Вроде я нашел такую траекторию. cos(x) там предел при подстановке сразу дает 1
Не понял, y = cos x ? Но cos x не стремится к 0 при x -> 0, поэтому это не траектория оканчивающаяся в нуле.
На какую траекторию?
>Вроде я нашел такую траекторию. cos(x) там предел при подстановке сразу дает 1
Не понял, y = cos x ? Но cos x не стремится к 0 при x -> 0, поэтому это не траектория оканчивающаяся в нуле.
>не стремится к 0
Ах, вот еще что должно быть. Ну тогда я не знаю такой путь, анон
Ну его придумать несложно (t cos(3pi/4+e^t-1), t sin(3pi/4+e^t-1)) например (в полярных координатах как раз r = t, phi = 3pi/4 + e^t -1, т.е. угол стремится к 3pi/4 быстро, а радиус стремится к 0 медленно). Предел даёт 1/sqrt(2)
ну нифига себе несложно, ты взял траекторию с параметром?
В смысле с параметром? Любая траектория - это пара функций (x(t),y(t)) образно говоря показывающая, какие у "частицы" будут координаты в момент времени t (только в нашем случае частица может двигаться "назад во времени", то есть t->0 справа).
Вот, даже график http://www.wolframalpha.com/input/?i=parametric+plot&a=C.parametric+plot-_Calculator.dflt-&f2=t+cos(3pi%2F4+%2B+e%5Et+-+1)&f=ParametricPlotCalculator.xfunction_t+cos(3pi%2F4+%2B+e%5Et+-+1)&f3=t+sin(3pi%2F4+%2B+e%5Et+-+1)&f=ParametricPlotCalculator.yfunction_t+sin(3pi%2F4+%2B+e%5Et+-+1)&f4=1&f=ParametricPlotCalculator.upperrange1%5Cu005f1&f5=-1&f=ParametricPlotCalculator.lowerrange1%5Cu005f-1&f6=t&f=ParametricPlotCalculator.variable1%5Cu005ft&a=FVarOpt.1-_-.ParametricPlotCalculator.variable2-.ParametricPlotCalculator.lowerrange2-.ParametricPlotCalculator.upperrange2--.ParametricPlotCalculator.zfunction---.*--
вот нарисованная траектория в вольфраме.
Вот, даже график http://www.wolframalpha.com/input/?i=parametric+plot&a=C.parametric+plot-_Calculator.dflt-&f2=t+cos(3pi%2F4+%2B+e%5Et+-+1)&f=ParametricPlotCalculator.xfunction_t+cos(3pi%2F4+%2B+e%5Et+-+1)&f3=t+sin(3pi%2F4+%2B+e%5Et+-+1)&f=ParametricPlotCalculator.yfunction_t+sin(3pi%2F4+%2B+e%5Et+-+1)&f4=1&f=ParametricPlotCalculator.upperrange1%5Cu005f1&f5=-1&f=ParametricPlotCalculator.lowerrange1%5Cu005f-1&f6=t&f=ParametricPlotCalculator.variable1%5Cu005ft&a=FVarOpt.1-_-.ParametricPlotCalculator.variable2-.ParametricPlotCalculator.lowerrange2-.ParametricPlotCalculator.upperrange2--.ParametricPlotCalculator.zfunction---.*--
вот нарисованная траектория в вольфраме.
Да, и предлагаю хотя бы проверить, что при подстановке в x и у вот тех вот выражений то в пределе t->0 получается не 0, а что-то ещё. Это не так сложно должно быть.
так, то есть траекторию еще можно кроме полярных и со временем брать? я просто не понимаю как ты это из головы взял
а стоп, если мы подставим эти траектории в предел там опять получится вид как в полярных координатах, t/cos(3pi/4+e^t-1)+ sin(3pi/4+e^t-1)
Любая траектория - это пара функций (x(t),y(t)) ты видимо думаешь, что траектории можно брать только вида (x,y(x)) но это не так, этот случай охватывает только траектории, которые могут быть представлены как графики функций.
>я просто не понимаю как ты это из головы взял
Соображения такие: для начала я перешёл в полярные координаты и получил
r/(cos a + sin a)
стало видно две вещи:
а) числитель и знаменатель можно стремить куда-нибудь отдельно
б) знаменатель обращается в 0 когда cos a + sin a = 0, тобишь когда a = 3pi/4
поэтому чтобы получить что-то "нетипичное" (не 0) нужно сделать две вещи: как можно медленне стремить числитель к 0 и как можно быстрее стремить а к 3pi/4. Ну я взял какую-то быстростремящуюся к нулю функцию e^t - 1 и записал
a = 3pi/4 + e^t -1
в качестве r я взял медленно стремящуюся к нулю функцию
r = t (хотя мог взять и r = t^(0.000001) тогда бы получил вообще бесконечность)
ну так что-то нетипичное и получил.
Типа да, осталось взять предел того что ты написал при t->0, можно разложить знаменатель в ряд тейлора до первого члена, например.
Пролопиталить можно кстати, и будет совсем просто.
Вот как. И если решить будет -1/sqrt(2). Ничего себе, спасибо, анон. Надо бы перекат сделать, я завтра приду с новыми задачами, объяснишь их?
Не знаю, если зайду, то постараюсь. Вообще есть dxdy.ru, правда они за LateX гоняют, но освоить его в сверхбазовом варианте - 10 минут делов.
Без аксиомы индукции (или ее аналога) довольно сложно дать определение натуральных чисел.
Но если, например, из аксиоматики Пеано выкинуть аксиому индукции, то можно построить довольно много структур, удовлетворяющих остальным трем аксиомам. Кроме того, возникает сложность с определением сложения. Корректность стандартного определения (по крайней мере, известного мне) использует аксиому индукции.
Если хочется как-то по-другому, то надо строго объяснить, что значит "запретить правило индукции".
У нас появятся "нестрогие" рассуждения из школьных учебников вида "повторяя подобные рассуждения, придём к выводу, что...", "и так далее, поэтому для произвольного n..."
Анон, нужна твоя помощь. Есть некая f(x), такая что f(x+1)=(f(x))^2
Более формально f(kx+a)=(f(x))^s^((k-1)n+a), но в моем случае я взял s равным 2. Так вот, рассмотрим равенство f(x+y)=f(x)^(2^y). Но в то же время x+y=y+x, а поэтому f(x+y)=f(y+x)=f(y)^(2^x). Далее, в ходе преобразований оказывается, что (ln(f(x))/2^x=(ln(f(y))/2^y
Теперь, собственно, сам вопрос: может ли это равенство быть верным для любых x и y, необязательно равных между собой, а то я туплю что-то?
Более формально f(kx+a)=(f(x))^s^((k-1)n+a), но в моем случае я взял s равным 2. Так вот, рассмотрим равенство f(x+y)=f(x)^(2^y). Но в то же время x+y=y+x, а поэтому f(x+y)=f(y+x)=f(y)^(2^x). Далее, в ходе преобразований оказывается, что (ln(f(x))/2^x=(ln(f(y))/2^y
Теперь, собственно, сам вопрос: может ли это равенство быть верным для любых x и y, необязательно равных между собой, а то я туплю что-то?
>f(x+1)=(f(x))^2
f(x) = 1, лол
А вообще f(x) = f(0)^(2^x). ln(f(x)) = 2^x ln(f(0)). Подставляй в свое равенство и убедись в том, что оно выполняется.
Но вообще ты не сказал, из какого множества у тебя x. Вещественное, целое, натуральное?
И саму задачу огласи. Люблю функциональные уравнения.
>f(x) = 1
Хм, а как это доказать, помимо банальной подстановки?
Вообще говоря, х можно считать вещественным, хотя в расчетах он не выходит на пределы натуральных чисел.
за пределы
Твоя функция однозначно строится из любой (не обязательно непрерывной) неотрицательной функции на [0..1) а затем достраивается по твоему уравнению на всё R. Собственно, решений аж целый гиперконтинуум.
>f(x+y)=f(x)^(2^y). Но в то же время x+y=y+x, а поэтому f(x+y)=f(y+x)=f(y)^(2^x). Далее, в ходе преобразований оказывается, что (ln(f(x))/2^x=(ln(f(y))/2^y
Такие преобразования справедливы для, хотя бы, целых x и y.
>Теперь, собственно, сам вопрос: может ли это равенство быть верным для любых x и y, необязательно равных между собой, а то я туплю что-то?
Вообще не понял вопроса, ну ты же сам и показал, что может (правда неявно предполагал x и у целыми).
>f(x+y)=f(x)^(2^y). Но в то же время x+y=y+x, а поэтому f(x+y)=f(y+x)=f(y)^(2^x). Далее, в ходе преобразований оказывается, что (ln(f(x))/2^x=(ln(f(y))/2^y
Такие преобразования справедливы для, хотя бы, целых x и y.
>Теперь, собственно, сам вопрос: может ли это равенство быть верным для любых x и y, необязательно равных между собой, а то я туплю что-то?
Вообще не понял вопроса, ну ты же сам и показал, что может (правда неявно предполагал x и у целыми).
>Хм, а как это доказать, помимо банальной подстановки?
Что доказать? Строчкой ниже я описал класс функций, которые тоже являются решением (f(0) можно брать любым). Вот возьми f(0) = 1 и будет у тебя f(x) = 1. Можно взять f(0) = 0 и будет f(x) = 0 - тоже подходит.
>Вообще говоря, х можно считать вещественным, хотя в расчетах он не выходит на пределы натуральных чисел.
Тогда давай и считать его натуральным, ибо чем шире множество, тем сложнее что-либо доказывать в таких задачах.
Так в чем задача-то? Ты так и не сказал.
>Твоя функция однозначно строится из любой (не обязательно непрерывной) неотрицательной функции на [0..1) а затем достраивается по твоему уравнению на всё R. Собственно, решений аж целый гиперконтинуум.
Это если ты говоришь о f(x+1)=(f(x))^2. А если о f(kx+a)=(f(x))^s^((k-1)n+a), то это, конечно, не так.
И вообще че-то ты где-то понаписал херни. Че за n? Это не x случаем? Потому что
f(kx+a)=(f(x))^s^((k-1)n+a) =>(k=1)=> f(x+a)=f(x)^(s^a).
a=1,x=0,k=1 => f(1) = f(0)^s
a=2,x=0,k=1 => f(2) = f(0)^(s^2)
a=0,x=1,k=2 => f(2) = f(1)^(s^n) = (f(0)^s)^(s^n) = f(0)^(s^(n+1)) => n+1 = 2, n = 1.
Аналогично при a=4,x=0,k=1 и a=0,x=2,k=2:
f(4) = f(0)^(s^4) = f(2)^(s^n) = f(0)^(s^(2 + n)) => n+2 = 4, n = 2 - противоречие с предыдущим равенством n = 1. Если же n поменять на x, то тут все будет нормально. Если так, то решением (возможно, не единственным) этого функционального уравнения будет f(x) = f(0)^(s^x), где в качестве f(0) можно брать любое число - подставь, убедись.
f(kx+a)=(f(x))^s^((k-1)n+a) =>(k=1)=> f(x+a)=f(x)^(s^a).
a=1,x=0,k=1 => f(1) = f(0)^s
a=2,x=0,k=1 => f(2) = f(0)^(s^2)
a=0,x=1,k=2 => f(2) = f(1)^(s^n) = (f(0)^s)^(s^n) = f(0)^(s^(n+1)) => n+1 = 2, n = 1.
Аналогично при a=4,x=0,k=1 и a=0,x=2,k=2:
f(4) = f(0)^(s^4) = f(2)^(s^n) = f(0)^(s^(2 + n)) => n+2 = 4, n = 2 - противоречие с предыдущим равенством n = 1. Если же n поменять на x, то тут все будет нормально. Если так, то решением (возможно, не единственным) этого функционального уравнения будет f(x) = f(0)^(s^x), где в качестве f(0) можно брать любое число - подставь, убедись.
Если через неделю никто не пересоздаст тред, то я сам его пересоздам, причём по своему усмотрению.
А картинку в оп-посте модеры стёрли, кстати?
>Че за n? Это не x случаем?
Да, это х. Ошибся при замене аргумента.
>Твоя функция однозначно строится из любой (не обязательно непрерывной) неотрицательной функции на [0..1)
Почему это? Если брать х равным, скажем, нулю, а y например 0,5, то можно навскидку привести несколько примеров, когда характеристическое уравнение не описывает выбранную функцию. sqrt(x), sin(x) и так далее. Или ты не об этом говорил?
>Такие преобразования справедливы для, хотя бы, целых x и y.
Собственно, это и есть главным вопросом. Не то, как найти функцию, а как доказать, что равенство может выполняться для x=/=y, при том не заменяя функцию частным значением ее же в какой-нибудь точке.
>(правда неявно предполагал x и у целыми)
Этот случай более чем очевиден, я потому его еще в условии исключил.
>Если так, то решением (возможно, не единственным) этого функционального уравнения будет f(x) = f(0)^(s^x), где в качестве f(0) можно брать любое число - подставь, убедись.
Вот тут понял, спасибо. Как нашел?
И это... неправильный ответ.
f(e^(x+1))!=(e^x)^2=e^(2x)
Надо прологарифмировать же. l=ln(f(x)
l(x+1)=2l(x) => по индукции на целых x: l=l02^x
обращаем логарифм возведением в степень
f(x)=e^(l02^x) - с точностью до основания логарифма т.к. его можно выбрать любым, т.е. дописываем константу к e - f(x)=Ce^(l0*2^x)
тьфу, константу я зря приписал - выбор основания закладывается через выбор l0 - a^l0=e^(lna*l0)
Откуда факториал взялся? Ннп вообще. И что значит l02? Про l=ln(f(x) понял. Лучше придерживайся привычных обозначений.











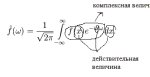








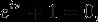










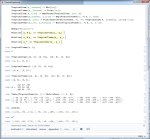

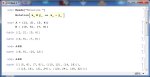

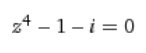















Точнее, публикации Суслина http://mi.mathnet.ru/inta100
Предыдущий: