Почему не бесконечный тред?
Мне там сказал в прошлом треде маняматик что нужно обязательно инетгрировать по лебегу, а как он не сказал.
Так как интегрировать по лебегу?
отсыпаешь простых функций, и складываешь их
Напиши мне пример как нужно.
Потому что тут могут быть различные ценные источники, информация, математические проблемы и прочее. В бесконечном треде это теряется.
Плохо понимаю обратную пропорциональную зависимость. Посоветуйте что-то.
Функция делится на коэффициент пропорциональности.
Планирую написать книжку по математики для дурачков. С чего начать?
Во сколько раз одна величина увеличивается, во столько другая уменьшается и наоборот.
Если серьёзно, то с арифметики.
С геометрии. Для всего указать геометрический смысл.
для простой ф-ции как ты хотел например x^2 просто поверни все набок и представь что интегрируешь по риману x=sqrt(y) на заданном интервале. то есть берешь предел суммы, но нарезаешь про горизонтали а не повертикали. в более сложных случаях нужно определять значения для measure u(E). есть аналогия про монеты - допустим тебе нужно посчитать сумму горсти монет разной стоимости. по риману ты суммируешь одну за одной, а по лебегу сперва сортируешь по номиналам, а потом суммируешь кучки.
У дурачков отсутствует абстрактное мышление. Следовательно, нужно начинать с какой-то конкретной проблемы - вычисления ящика, например.
Какие кучки монет, не понял про кучки, разве можно так сравнивать. И что значит "положить набок" с мат т.з.
Дайте советов мудрых по изучению геометрии (планиметрия для начала, хотя бы).
линейная алгебра
Рано пока, наверное, хотя в виде отрывочных фактов я и знаю немного о ней. Я пока хочу такую более "простую" и при чем в качестве последовательных выводов каких-то, а это сложно, так как я не люблю геометрию и нет такого, эм, "геометрического мышления", если брать термин из воздуха. Вооот. Очень плохо в геометрии на данный момент понимаю, из разных источников узнаю, что судя по всему ниже среднего.
набок y^-1 - обратная ф-ция.
кучки монет см график. по х - каждая монета. по y - ее стоимость. допустим 3 значения 1 2 3 руб.
по риману суммируешь все монеты по очереди 1+3+2+1+1+3+2+2. по лебегу - горизонтальные линии показывают кол-во монет каждого номинала. поэтому суммируешь 1р x3 + 2р x 3 + 3p x 2. то же самое для x^2. суммируешь по у, то есть берешь предел суммы u(E)*dy для обратной ф-ци y^-1 что есть x=sqrt(y). в обоих случаях каждого такого интервала - присваивается значение measure u(E). как это сделать не всегда очевидно, но для простых функций типа y=x^2 u(E) это просто значение обратной ф-ции. а вот для монет как раз для каждого (дискретного) значения y присваивается measure - в данном случае кол-во монет данной стоимости.
Ящик таполаги вычислить не смогли.
Тобишь лебезгование это интегрирование обратной функции?
Я думал тут какая то жопоебля нужна будет, с нахождением минимальных значений и прочим
Решили же. n-мерная сфера при n в бесконечность.
Не всё так просто. У тебя обратная функция может оказаться многозначной.
Что то книжку писать нихуя не просто. Начал писать про числа и как то расплылся на пять страниц нихуя конретного не описав, кроме как "числа это как бы счет на пальцах".
Очевидно же что с введения понятия числа.
Это сразу после/вместе с базовой арифметики/ой. Ведь по сути это же просто разные отображения одного и того же предмета/явления, ящитаю.
Очевидно же что с введения понятия числа.
Это сразу после/вместе с базовой арифметики/ой. Ведь по сути это же просто разные отображения одного и того же предмета/явления, ящитаю.
А еще там обнаружили что при таком подходе будет алюминий экономится ведь мы будем делать ящик из фанерки
Интегрируем по всем отрывкам жэ, нет?!
> на интервалы разбивают её область значений, а затем суммируют с соответствующими весами меры прообразов этих интервалов.
Вот это меня просто напрягло. Как я разбивать на область значений буду то?
легко там подумать, но это только в простом примере. поэтому это не очень удачный пример.
Ну давай, расскажи мне тогда про общий случай.
>расплылся на пять страниц нихуя конретного не описав, кроме как "числа это как бы счет на пальцах".
Когда пишешь всегда держи в уме - для кого ты пишешь (что целевая аудитория знает на данный момент и какое минимальное количество знаний необходимо приобрести для перехода на некоторый следующий этап), ну и естественно "цель" - что из себя представляет этот самый следующий этап изучения. Т.е. не ударяйся в "философию" и не пытайся просто излагать всё что ты знаешь/слышал/думаешь на тему N.
> не пытайся просто излагать всё что ты знаешь/слышал/думаешь на тему N.
Наоборот, живой язык, смешнявочки в перемешку строгими терминами, быдлу нравица, тяночки текут, гаусс грит малаца, все правельно сделол.
НУ и да, я пытаюсь пояснить так чтобы даже алкаш васян понял что три бутылки на двоих это лучше чем четыре на троих, потому и словесный понос у меня получается
Ну или я сам нихуя не знаю, но решил что я непризнанный математик.
Как понять геометрию?
Начертить все
Как лучше научиться чертить?
Аноны, нужно было в учебнике по Тригонометрии доказать, что тангенс альфа > угла альфа. Была дана подсказка - сравнить площади сектора и прямоугольного треугольника. Я сделал немного по-другому: провел перпендикуляры к основанию AC, катету BC и составил неравенство.
(1-HC)(BC-BK) / 2 > BC / 2
Поскольку, 1 > (1-HC), а BC > (BC-BK), то неравенство ложное, а значит S треугольника > S сектора. И вот скажите правильно хоть что-то у меня вышло или это полный бред? Никогда не умел доказывать, пытаюсь что-то сформировать из уже прочитанного.
(1-HC)(BC-BK) / 2 > BC / 2
Поскольку, 1 > (1-HC), а BC > (BC-BK), то неравенство ложное, а значит S треугольника > S сектора. И вот скажите правильно хоть что-то у меня вышло или это полный бред? Никогда не умел доказывать, пытаюсь что-то сформировать из уже прочитанного.
>(1-HC)(BC-BK) / 2 > BC / 2
Ты сравниваешь площадь с длиной
А то что тангенс сравнивается с углом ничего?
>доказать, что тангенс альфа > угла альфа
в смысле безразмерный тангенс > угла в градусах?
Есть радианная мера угла.
Почему с длиной? Там ведь основание единице равно и я его опустил просто в правой части или ты про что-то другое?
Да, видимо, безразмерный тангенс, т.к. просто сказано доказать неравенство.
В универе теорвер преподавал ретард, но знать его все-же хочется. По сему прошу помощи у здешних. Посоветуйте, добрые люди, книжек или курсов каких. Желательно с упором на прикладные задачки, ибо по теории упарываться одной не результативно.
Добрый вечер, анонимы.
Летние каникулы, занимаюсь математикой по Ткачуку ("Математика для абитуриентов"), дошёл до шестого урока (системы тригонометрических уравнений) и всё плохо получается. В школе как таковой этой темы не было. Знаю, что обычная система, но всё равно додуматься не могу. Прошу о помощи (фото прикреплены). Есть какие-то хаки в работе с такими вещами?
Заранее благодарю
Летние каникулы, занимаюсь математикой по Ткачуку ("Математика для абитуриентов"), дошёл до шестого урока (системы тригонометрических уравнений) и всё плохо получается. В школе как таковой этой темы не было. Знаю, что обычная система, но всё равно додуматься не могу. Прошу о помощи (фото прикреплены). Есть какие-то хаки в работе с такими вещами?
Заранее благодарю
>Почему с длиной? Там ведь основание единице равно и я его опустил просто в правой части
Тогда всё хорошо.
>Поскольку, 1 > (1-HC), а BC > (BC-BK) то неравенство ложное
Верно
>а значит S треугольника > S сектора
Нет. У тебя площадь сектора = (1-HC)(BC-BK)+S(MCH).
И вообще, с чего ты взял, что если площадь сектора меньше площади треугольника, то тангенс меньше радиуса? Попробуй сначала это доказать.
Почти не понимаю геометрических теорем, а доказать что-то самому вообще сверхзадача. Посоветуйте что-то.
>меньше
больше, быстроfix
Евклидова геометрия скучная хуйня. Советую забить.
Самому не нравится, но хочется знать какие-то основы так сказать. Да и многие говорят о какой-то там геометрической интуиции. Как же быть со всем этим?
Если ты в школе, то начни читать учебник с начала. Если уже начал, то попробуй другие.
Вентцель, 'теория вероятностей'.
2.5x + 5 = 3(x-5)
В Сканави Элементарная математика есть базовая информация по геометрии, там её прочти да и все.
Что то не получается книжку написать свою личную.
Может тупо взять и переписать какой то сборник бурбаков на простом и доступном языке!?
Может тупо взять и переписать какой то сборник бурбаков на простом и доступном языке!?
Не трать время. Давно уже всё в книгах написано и в гугле. Можешь только заполнить некоторые школьные пробелы. Напиши о правиле переноса, например; меня заставляли заучивать его словами, как и решения простейших уравнений, типа чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемоеучили это словами как стихотворение; думаю не меня одного. Перед этим напиши, что означает знак равно. Напиши так же, почему сложение-умножение уголком даёт верный результат. Почему при сложении дробей нужно привести к общему знаменателю, и почему при умножении этого делать не надо. О сечениях Дедекинда, можешь скопипастить с оригинал текста, его любой человек поймёт.
Как же сложно.
Суть в том чтобы написать цельный курс от счета на пальцах до топологических бесконечномерных многообразий. Чтобы не было такого, что в одном учебнике учат считать яблоки, а в следующем по сложности сразу матрицы в детерминанты скручивать подразумевалось само собой разумеющимся.
Что-то я нихрена не понел. почему 3(x-5) в скобках?
1)2.5x; y; из условия неизвестно какая пачка к какой принадлежит.
2)Я так понял здесь из разряда элементарной логики? Типа -5 тетрадей переложили значит с 2.5, до 3 раз опустилась?
3)y-5=3x
Ну можно еще x + 5 = 3(2.5x - 5), но ответ будет не целый. Перемещение подразумевает, что из одной пачки вычли, ко второй прибавили.
И игрек тебе не нужен. В одной пачке x, во второй 2.5x.
Помогите.
Позже попробуй помочь.
Спасибо.
Не так уж всё и сложно. Смотри:
An образуется по формуле: n-e Число Каталана a^n
Пример:
1 a = A1
1 a^2 = A2
2 a^3 = A3
5 a^4 = A4
14 a^5 = A5
42 * a^6 = A6
Где 1, 1, 2, 5, 14, 42... - числа Каталана
По идее ответом будет бесконечность, так как корень n степень из n-го числа Каталана - возрастающая функция
Думаю, в решении этой задачки должен также быть задействован формальный степенной ряд. Только непонятно, как его встроить в эту задачку.
Я этот анон, применяя асимптотическую формулу с педивикии
Вот это похоже на правильный ответ.
Спасибо!
Поясните мне как вывести формулу ряда для экспоненты?
Доказательство же в рандом учебнике матана.
сап чуваки. не подскажете маршрут изучения и соотв. лит-ру чтоб в конечном итоге добраться до когомологий галуа
Я его не понял раз спрашиваю.
Давай скрины из учебника, за одно скажешь, где непонятно.
Вверху списки.
Котаны-матаны, поясните пожалуйста дурачку, что такое меры Лебега и Жордана? Читаю определение и нихуя не могу ни представить, ни понять. Может ли кто-нибудь объяснить эти вещи на бытовом языке, так чтобы можно было их "пощупать"?
Берем ограниченную фигуру. Покрываем её всё более и более мелкими прямоугольниками. На каждом шаге вычисляем их суммарную площадь. Берем инфимум. Это внешняя мера Жордана фигуры.
Берем ограниченную фигуру. Вписываем в фигуру прямоугольники всё более и более мелкой площади. На каждом шаге вычисляем их суммарную площадь. Берем супремум. Это внутренняя мера Жордана фигуры.
Если внутренняя и внешняя мера Жордана фигуры равны, то это число называется просто мерой Жордана, а фигура - измеримой по Жордану.
---
Берем ограниченную фигуру. Покрываем её всё более и более мелкими прямоугольниками. На каждом шаге вычисляем их суммарную площадь. Берем инфимум. Это внешняя мера Лебега фигуры.
Берем ограниченную фигуру. Описываем вокруг неё прямоугольник. Берем разность "прямоугольник минус фигура". Берем внешнюю меру этой разности. Вычитаем её из площади прямоугольника. Получится число. Оно называется внутренней мерой Лебега фигуры.
Если внутренняя и внешняя мера Легеба фигуры равны, то это число называется просто мерой Лебега, а фигура - измеримой по Лебегу.
"Спасибо" колоссальных размеров направляется в твою сторону, анон!
Все непонятно.
Откуда её вообще взяли непоняно.
>делимость чисел
>если сумма всех цифр числа делится на 3 или 9 то все число соответственно делится на 3 или 9
>если разница между последними тремя числами числа и всеми остальными числами делится на 7, 11 или 13 то все число делится на 7, 11 или 13
>на 8 или 125 делятся те числа у которых число трех последних цифр делится на 8 или 125
КАК? Откуда эти свойства повыползалии почему они правильные?
>если сумма всех цифр числа делится на 3 или 9 то все число соответственно делится на 3 или 9
>если разница между последними тремя числами числа и всеми остальными числами делится на 7, 11 или 13 то все число делится на 7, 11 или 13
>на 8 или 125 делятся те числа у которых число трех последних цифр делится на 8 или 125
КАК? Откуда эти свойства повыползалии почему они правильные?
Правильные, потому что можно доказать. Пруфы легко гуглятся.
Теорема пирожного безе
Что значит deg?
Обычное сравнение по модулю.
Число равно нулю mod n тогда и только тогда, когда оно делится на n.
10 = 1 mod 9.
10^n = 1 mod 9 для любого натурального n.
Поэтому
a10^n + ... + b = a + ... + b mod 9.
На самом деле все такие "признаки" можно изобретать чисто механически. Каждый признак - всего лишь утверждение, что одно число равно другому числу по mod такому-то.
>Число равно нулю mod n тогда и только тогда, когда оно делится на n.
Чего чего?
Модуль -9 равен 9.
|-9|/9=1
Не путай модуль и сравнение по модулю. Два принципиально разных понятия, по недоразумению называющиеся похожими словами.
В чем тогда разница, я не понял.
Как-нибудь докажи, что ты не тролль. Мне лень печатать.
Я из школы просто капчую. Знаю что такое модуль, абсолютная величина числа, а сравнение по модулю не знаю.
Ну окей.
Есть такая штука - сравнение по модулю n. Где n - целое положительное число.
Тут "модуль n" - просто слова, сами по себе ничего не означают.
Суть в том, что любое целое число надо заменить его остатком от деления на n.
Оказываются, что при этом сохраняются сложение, вычитание и умножение.
Например, рассмотрим арифметику по модулю 5.
Числа этой арифметики будут 0, 1, 2, 3, 4.
Тогда, например, [1023] = [28] = 3 (mod 5), потому что все эти числа дают один и тот же остаток при делении на 5.
[3][3] = [3*3] = [9] = 4 (mod 5)
[1023][28] = [3][3] = 4 (mod 5)
[1023] + [28] = [3 + 3] = [6] = 1 (mod 5)
1+1+1+1+1 = 0 (mod 5)
Число равно нулю mod 5 тогда и только тогда, когда остаток от деления этого числа на 5 равен нулю.
Т.е. когда число делится на 5.
Как интеграл пикрелейтед вычислили? Что за z? Это замена какая-то?
А интеграл Лебега, следовательно, определен через меру Лебега?
Т.е. где у Римана стоят пределы интегрирования, у Лебега - мера, которая понимается, как обобщения понятия длины отрезка? Запутался
а делить на число в арифметике по модулю p можно тогда и только тогда, когда оно взаимно просто с p?
deg(P(x)) означает степень многочлена P(x)
Болтянский 3 проблема Гильберта
Аноны кто-нибудь может объяснить на пальцах почему public key cryptography работает? Любую объяснения начинаются с очевидно факта что два больших простых числа легко умножить но сложно разложить на множители. Но это же только начало. А потом начинаются какие-то дебри с e и d и модулями. Почему это все работает?
не могу понять что значит x1, x2, ... - случайные величины, в теореме Чебышева.
при определении говорят: x1, x2, ... - случайные величины.
случайная величина, это функция: f : S -> N
S -- множество исходов.
доказывается, что P({ |1/n sum(x_i, i от 1 до n) - a| < z }) -> 1
что значит: x1 + x2 + ... + x_n?
т.е. я понимаю нотацию для одной случайной величины:
P({ w из S : X(w) < 3 }) эквивалентно P({X < 3}).
и неравенство Чебышева понятно.
2. мне понятна теорема если x1, x2, ... это __значения__ случайной величины X.
т.е. x1 = X(E_j), x2 = X(E_i), ....
X - случ. величина. E_j и E_i - нам не известные исходы.
при определении говорят: x1, x2, ... - случайные величины.
случайная величина, это функция: f : S -> N
S -- множество исходов.
доказывается, что P({ |1/n sum(x_i, i от 1 до n) - a| < z }) -> 1
что значит: x1 + x2 + ... + x_n?
т.е. я понимаю нотацию для одной случайной величины:
P({ w из S : X(w) < 3 }) эквивалентно P({X < 3}).
и неравенство Чебышева понятно.
2. мне понятна теорема если x1, x2, ... это __значения__ случайной величины X.
т.е. x1 = X(E_j), x2 = X(E_i), ....
X - случ. величина. E_j и E_i - нам не известные исходы.
Посоветуйте книги по геометрии начиная с введения для дошкольников, и всё это дабы потом от зубов отскакивало, если что.
Для дошкольников не нужны, начинай с 7 класса. Курсов геометрии не так много, полистай все, которые найдёшь, какой-нибудь понравится больше. Ну и главное задачки не пропускай.
>всё это дабы потом от зубов отскакивало
В элементарной геометрии только о биссектрисе дохуялион теорем, ты их никогда не выучишь. Прочти про теорему Пифагора, про движения и тригонометрию. Больше ничего не нужно, если ты не историк.
Народ привет:-) в школе хорошо шла математика, всегда на отлично, но я ушел учиться на другую профессию и математику совсем позабыл, решил наверстать упущенное и узнать новое, кто знает, может я не ту профессию выбрал. Посоветуйте хороших учебников начиная со школьной скамьи и до более серьезной подготовки, прошу вас, уважаемые
Ну начать следует с самого простого - с арифметики конечно. Рекомендую "Курс арифметики" Жан-Пьера Серра, но если даже это не пойдёт, то советую забить на метематику
Нужно научится оптимизировать маршрут развоза хуйни по точкам. Это теория графов как я понял. Какой учебник нужен для закатывания в неё?
Спрошу здесь, ибо это скорее математика, чем программирование.
Каноническая разметка графа это некоторый алгоритм нумерации его вершин. При этом для двух изоморфных графов каноническая разметка должна дать один результат.
Задача: придумать алгоритм канонической разметки для множества ненаправленных не содержащих узлов раскрашенных (раскрашены как вершины, так и ребра) графов, у которых не более одного цикла.
Я придумал (стырил) алгоритм канонизации раскрашенных деревьев за O(n). При том у дерева может быть одна помеченная точка, а может не быть.
Алгоритм для графа придумал такой:
1. Находим цикл.
2. Удаляем его. Помечаем вершины, входящие в цикл.
3. У нас получается дизъюнктное объединение деревьев. Каждое из них канонически размечаем.
4. Теперь у нас есть разметки деревьев (каждое дерево помечено числами 0, 1, ..., l, где l - числовершин дерева). Сортируем деревья (для этого можно взять любое отношение порядка на деревьях, плевать). Нулевое дерево нумеруем с 0, первое -- с (число вершин нулевого дерева), второе -- с (сумма числа вершин нулевого и первого деревьев) и так далее.
Итого получается время работы за O(n log n) из-за сортировки. А мне сказали, что можно сделать за линию и что сортировка не нужна:
> ... Однако потом нам нужно сравнить коды для каждой компоненты связности и рассортировать их, а это минимум O(N log N), N -- число компонент связности.
> Это можно сделать за O(N). В программе реализовывать необязательно, но знать необходимо. Это классический алгоритм, есть во всех учебниках.
Что за алгоритм от меня хотят?
Тут же задача, эквивалентная задаче сортировки. Такое не делается за линию!
Каноническая разметка графа это некоторый алгоритм нумерации его вершин. При этом для двух изоморфных графов каноническая разметка должна дать один результат.
Задача: придумать алгоритм канонической разметки для множества ненаправленных не содержащих узлов раскрашенных (раскрашены как вершины, так и ребра) графов, у которых не более одного цикла.
Я придумал (стырил) алгоритм канонизации раскрашенных деревьев за O(n). При том у дерева может быть одна помеченная точка, а может не быть.
Алгоритм для графа придумал такой:
1. Находим цикл.
2. Удаляем его. Помечаем вершины, входящие в цикл.
3. У нас получается дизъюнктное объединение деревьев. Каждое из них канонически размечаем.
4. Теперь у нас есть разметки деревьев (каждое дерево помечено числами 0, 1, ..., l, где l - числовершин дерева). Сортируем деревья (для этого можно взять любое отношение порядка на деревьях, плевать). Нулевое дерево нумеруем с 0, первое -- с (число вершин нулевого дерева), второе -- с (сумма числа вершин нулевого и первого деревьев) и так далее.
Итого получается время работы за O(n log n) из-за сортировки. А мне сказали, что можно сделать за линию и что сортировка не нужна:
> ... Однако потом нам нужно сравнить коды для каждой компоненты связности и рассортировать их, а это минимум O(N log N), N -- число компонент связности.
> Это можно сделать за O(N). В программе реализовывать необязательно, но знать необходимо. Это классический алгоритм, есть во всех учебниках.
Что за алгоритм от меня хотят?
Тут же задача, эквивалентная задаче сортировки. Такое не делается за линию!
понял так:
x1, x2, ..., x_n - результаты попыток.
как в 2., x1 = X(E_j), а так-как E_j не известно, то это и значт, что x1 = X.
далее понятно, что если
Y = (x1 + x2 + ... + x_n)/n -- среднее арифм.
то M(Y) = M(X), где M - ожидание.
...
Пожалуй, можно более простую формулировку дать.
Есть круг. На круге N пометок: a_1, ... a_N. Придумать алгоритм нумерации пометок, такой, чтобы при повороте круга и отражении пометкам соответствовали те же числа.
Чет через задницу объяснил. Надеюсь, кто-нибудь поймет.
Пытался выразить через формулу суммы геометрич. прогрессии, но упростить ничего не вышло. Либо я не очень понимаю, что именно должно быть в итоге. Решаю упражнения из книжки «Что такое математика» (Курант, Роббинс), но там нет решений или ответов.
Не нужно упрощать ответ, это формальное задание и в ответе будет фигурировать дробь в n-ной степени.
x1 + x2 + ... + x_n сумма функций. Внезапно, она тоже функция.
Спасибо, посоны, я придумал.
Анон, предположим, что у меня есть функция, которая является комбинация других функций f1(f2(..fn(x)..),...,fm(..)) Как мне найти их степень влияния, если комбинации не строятся через суммы как в рядах Фурье? Есть что можно почитать по этому поводу?
Функция от функции функции под функцией внутри функции функции внутренней функции?
Берешь первые две дроби. Вычисляешь их. Смотришь какой результат они дают в итоге.
Берешь три первые дроби. Смотришь какой результат они дают в итоге.
Строишь гипотезу что они дают какую то там функцию зависящую от количества взятых дробей.
Вычисляешь сумму дробей в лоб и по твоей найденное формуле-гипотезе. Сравниваешь результаты. Если они совпадают значит гипотеза правильна. Если нет возврат к шагу один.
Расскажите, пожалуйста, о том как у вас устроена память на математическую информацию и как вы ее вытягиваете.
На самом деле неплохо бы вектор-функции. Все функции известны. Каждая характеризуется своим отображением и весом влияния, т.е. если вес ноль, то F(x,0) = x. (или не ноль, просто нейтральный элемент) Что-то типа этого. Нужна как методик их построения, так и интерполяция ими через поиск весов, но функции не суммовые, т.е. что-то сложнее ортогональных функций.
Буду рад любой зацепке.
Матемачую. Я не тролль.
на самом деле в введении написано, для кого эта книга
Вопрос такой:
Пусть есть изображение с камеры, слева на пикрил, и есть фактическая расстановка, справа (вид сверху). Очевидно, что эти две фигуры будут подобны. На фото есть два квадрата известного реального размера. Расстояние между ними также известно, поэтому мы можем определить все "верхние" значения. Как найти хотя бы высоту? Имеет ли отношение ко всему этому фокусное расстояние камеры? Или как по картинке с камеры определить расстояние до них?
Пусть есть изображение с камеры, слева на пикрил, и есть фактическая расстановка, справа (вид сверху). Очевидно, что эти две фигуры будут подобны. На фото есть два квадрата известного реального размера. Расстояние между ними также известно, поэтому мы можем определить все "верхние" значения. Как найти хотя бы высоту? Имеет ли отношение ко всему этому фокусное расстояние камеры? Или как по картинке с камеры определить расстояние до них?
Как решать такую задачку:
100 человек едят торт.
Первый съел 1% от торта
Втрой съел 2% от оставшегося после первого куска
Третий - 3% от оставшегося после первых двух и т.д.
....
Сотый съел оставшийся кусок целиком
Кто съел самый большой кусок торта?
Мне не нужен ответ на задачу, я хочу понять, как её решить. Простой арифметикой я состарюсь, пока решу.
100 человек едят торт.
Первый съел 1% от торта
Втрой съел 2% от оставшегося после первого куска
Третий - 3% от оставшегося после первых двух и т.д.
....
Сотый съел оставшийся кусок целиком
Кто съел самый большой кусок торта?
Мне не нужен ответ на задачу, я хочу понять, как её решить. Простой арифметикой я состарюсь, пока решу.
(1-1%)-2%)-3%)-...
А если я еще не дошел до этого курса? До него что нужно узнать подучить?
Каких чисел больше, рациональных или иррациональных?
>The standards texts (Stewart, Rogawski, et al.) you see required for college classes are, in all honesty, quite terrible since they are not written with self-study in mind but just as a collection of exercises and a review of the basic methods.
Щито? Диды училесь а форчематеки носом крутят и ничего лучше не предлагают.
Поровну.
Иррациональных. Они равномощны действительным и потому не являются счётными, а рациональные можно сосчитать.
Дурной? Бесконечность тех и тех.
Пруфы билли.
Особенно тут
>равномощны действительным и потому не являются счётными
>Бесконечность тех и тех.
Боюсь доказать невозножно, как и то, что бесконечно много натуральных, из которых бесконечно можно получать и те и другие.
Множество рациональных чисел счётно.
Объединение счетного числа счётных множеств счётно.
Если A не счетно и B счётно, то A+B счётно.
R = Q+(R\Q)
Т.к. R не счетно, то Q\R не счётно.
>Если A не счетно и B счётно, то A+B счётно.
несчётно
быстрофикс
>Т.к. R не счетно, то Q\R не счётно.
R\Q
2-ой быстрофикс
>бесконечно много натуральных
Никто не запрещает добавлять один к любому числу.
И как ты мне из натуральных получишь гомогейские иррациональные?Один на три делить будешь?
Можно кстати просто доказать, что если A несчётно и B счётно, то A\B несчётно.
>И как ты мне из натуральных получишь гомогейские иррациональные?
Извлечением корня.
как епта выучить всю логику чтобы епта без хуйни
>Если есть гомотопии, то должны быть и гетеротопии.
В бе не помогли:
Есть кводрат со стороной а. Делим пополам по диагонали. Известно, что сумма сторон получившегося треугольника равна 24. Нужно найти а, с.
2а + с = 24
2а^2 = c^2
2a^2 = (24 - 2a)^2
a^2 - 48a + 288 = 0
Пытаюсь решать, получается какая-то хуйня, подскажите, где я обосрался.
Есть кводрат со стороной а. Делим пополам по диагонали. Известно, что сумма сторон получившегося треугольника равна 24. Нужно найти а, с.
2а + с = 24
2а^2 = c^2
2a^2 = (24 - 2a)^2
a^2 - 48a + 288 = 0
Пытаюсь решать, получается какая-то хуйня, подскажите, где я обосрался.
Сап, не подскажете в каком направлении копать, чтобы решить эту помойку?
Интересно, как доказать, что множество алгебраических чисел счётно, по индукции. Какие ещё есть доказательства, кроме биекции?
Сходится. А как это твоя машина посчитала? Интегралы какие-то, я же в этом нихуя не понимаю. Почему квадратным уравнением не получилось?
>Почему квадратным уравнением не получилось?
Получилось, именно им. Просто ты в расчётах корней где-то накосячил
Спасибо, буду проверять.
Анончики, которые читали Шварца, уже хорошо зная курс анализа, как ощущения? Я в топологии 0, интересно посмотреть как тут все выводится.
Анончик, послушай мой бред. В бесконечном множестве натуральных чисел, содержится бесконечно много простых чисел. => из бесконечного числа простых чисел, можно составить бесконечное число пар. Собственно, в бесконечном множестве пар, найдется такая (там же вроде как должна быть любая, раз вариантов бесконечность, это как содержание чего угодно в остатке от деления пи), которая сможет представить, например с помощью суммы, элемент кхм совместимого бесконечного множества(множество натуральных не содержит противных простым элементов (всяких там вещественных, мнимых и тд, т.е их можно получить из простых, без использования деления)).
Вопрос тут только в том, требуется ли доказывать что, в бесконечном множестве пар, найдется любая пара. Или это это является доказанным?
Вопрос тут только в том, требуется ли доказывать что, в бесконечном множестве пар, найдется любая пара. Или это это является доказанным?
>кхм совместимого
Что это?
Внутренние определение, которое я дальше пытаюсь дать (в скобках). Для умножения это доказанно, значит множество нам подходит.
Я пытаюсь сказать, что в бесконечном множестве вариантов, найдется нужный нам, так как он не требует элементов, не содержашихся в исходном множестве (простых чисел).
Чел, я не знаю, у тебя проблемы с речью вообще или только по математике, но если второе, тебе нужно больше решать задачи, не пропуская формальности, потому что ты выражешься очень плохо. Если я тебя понял, ты хочешь сказать, что каждой паре простых чисел можно сопоставить, например, вещественные числа. Это не так. В первым месяц на любом факультете, связанном с матешей, проходят это. Погугли "доказательство несчетности множества вещественных чисел" или прочитай его в любом введение любого учебника по матану.
Как раз таки вещественные нельзя. Тут должна была быть тонкая шутка о проблеме Гольдбаха, но судя по всему, математику я и правда позабыл.
1)Масса одного красного ящика была в 1.5 раза больше чем масса синего ящика.
Как это записывать с мат точки зрения? Можно считать что 1.5x=y?
ОМГ, какой же безумие.
1)За x берем кол-во тетрадей в обоих пачках. Ок
2)В одной 2.5x в другой x
3)2.5x-5=3x-5
ОТКУДА У ТЕБЯ ЭТИ СКОБКИ?
Разве так вообще можно? Нужно же брать в одной пачке x в другой y.
Ананасы, как для интеграла указать ограничение по оси y? То есть есть функция 1-x^2 и 3 ограничения: x1=-2, x2=0, y=0. x1 и x2 идут в качестве входных параметров первообразной функции, а вот y куда?
Что такое x1 и x2? Как это связано с x в строке 1-x^2.
Как без производной найти область значений функции?
y=sin(x)-sqrt(3)cos(x)
y=sin(x)-sqrt(3)cos(x)
Область значений должна быть дана по определению функции.
Это такое задание.
Область значений функции - это такие числа, которые вообще могут получится при вычислении этого выражения. Методом вспомогательного аргумента сворачиваешь выражение к виду A sin(p) и вспоминаешь, что синус принимает значения [-1; +1]. Соответственно, A sin(p) будет принимать [-A; +A]. Суть задания в методе вспомогательного аргумента, и это очень часто используется в тригонометрии. луркай
Здесь предполагается, что я еще не знаком со вспомогательным аргументом.
Тут производная и в помине не нужна. Надо просто уметь складывать синус и косинус от одного угла.
В таком случае, уточняй у преподавателя что он от тебя хочет, мы тут не бабы Ванги.
Предполагается, что я знаю только формулы сложения, т.е sin(a±b), cos(a±b), tg(a±b), ctg(a±b)
Раздели на 2 и умнож на 2. А после воспользуйся формулами сложения. sqrt(3)/2 и 1/2 - значения косинуса и синуса одного угла.
y=1-x^2
x=-2
x=0
y=0
вместе эти четыре линии формируют как бэ фигуру с кривым верхом. задача - найти площадь этой фигуры.
ну стандартная задача, в общем
Как быстро наверстать упущенное в школе?
С какого места и для каких целей?
Никак
присоединяюсь к этому посту,
наверстать геометрию, начиная с 7 класса. (именно практика, решение задач)
Из треда в тред... Школа хуита, поэтому наверстывать и ориентироваться на неё не нужно. Если ты школьник, то забей на школо-матешу, если нет, то тем более тебе это не нужно.
Посмотри Шень "Геометрия в задачах“
Лучше сразу гомотопии с кольцами изучать, да?
Да. Лучше бы это в старшей школе начинали учить
примерно за 3 месяца прошел почти весь школьный курс. производные и первообразные на русском ютубе, все остальное с ханакадеми. не прошел только стереометрию и малую часть геометрии. на кханакадеми тупо формулы по стереометрии, а на русском слишком сложна.
Где? В школе? В школе не должно быть математики. Ни такой какая она сейчас, ни гомотопий с кольцами. С чего нужно начинать уже тысячу раз писали -Шень "Алгебра" и "Множества", Алексеев "Теорема Абеля".
И как школьники будут без геометрии?
Зачем она?
Так надо.
Нет. Из всей доисторической геометрии пригодиться только теорема Пифагора.
Пизда.
Диды строили радиосистемы геолокации с помощью конических сечений времен архимеда, а гомолог над кольцами говорит что они хуйня нужно и теорему абеля дрочить.
Я даже и не знаю это тролинг, тупость или тролинг тупостью...
Диды строили радиосистемы геолокации с помощью конических сечений времен архимеда, а гомолог над кольцами говорит что они хуйня нужно и теорему абеля дрочить.
Я даже и не знаю это тролинг, тупость или тролинг тупостью...
Мы говорим о школьниках. Школьники не будут "строить радиосистемы геолокации с помощью конических сечений времен архимеда". У них есть более важные дела - выучить английский, например.
http://dxdy.ru/topic68329.html
Только гляньте, как тут проводятся по губам всем тем, кто говорит, что на калькуляторе калькусул решать надо.
Только гляньте, как тут проводятся по губам всем тем, кто говорит, что на калькуляторе калькусул решать надо.
Нет, у них самые главные дела поцеловаться и поебаться самым первым в классе.
Вы хоть предупреждайте о перекатах.
А реально, чего так? Почему комплюктер посчитать не может? Это такая подлянка от одной культуры другой?
Нам нужен программист чтобы разобраться. Есть тут такие которые могут код мапла/математики декомпилировать и глянуть что там такое интересное.
Мы на /math, поэтому пришедшим сюда интересна математика. Дедам, строившим радиосистемы геолокации математика не была интересна сама по себе.
Я выше написал, что нужна только теорема Пифагора. Чтобы её доказать, нужно знать о треугольниках и о подобиях. Поэтому я не утверждаю, что всю евклид. геом. учить не нужно. Конечно, нужна ещё, к примеру, тригонометрия, но её проще учить через алгебру.
В школе никакую математику, кроме счёта, преподавать не нужно. Школьники делятся не только на строителей систем геолокации и математиков, а ещё и на юристов, врачей, музыкантов... Я бы не хотел, чтобы меня в школе насильно учили нотам и игре на каком-нибудь инструменте, точно так же музыканты не хотят учить конические сечения. Да и с инструментами получилось бы хуего, я бы с трудом играл. С математикой точно так же, вчерашние выпускники не знают вообще нихуя. Так нужно ли тратить время и нервы? Нет.
Математика в школе не для того, чтобы потом идти в универы.
А для чего? Только пожалуйста без "ум в порядок приводит".
Но она именно для этого. Как и все остальные науки. Геометрия вот нужна для умения логически обосновывать свое мнение и ее упадок явно связан с тем, что сейчас в нашем обществе происходит.
Если бы математику в школах учили только для универа, то после 7 класса имело бы смысл убрать ее у всех, кроме одного профильного класса, а с ним гнать в два раза быстрее.
Вопрос такого рода(я толком-то и не знаю как его сформулировать):
Какая общая идея объединяет различные виды(типы) сходимостей?
(по метрике, поточечная и т.д. + в теории вероятностей)
Какая общая идея объединяет различные виды(типы) сходимостей?
(по метрике, поточечная и т.д. + в теории вероятностей)
А мужики то и не знают. Беги им сообщать быстрее.
Для тебя, дебилоида покалеченного гомологическими пучками на модулями колец бесконечномерных пространств, так и быть, объясню. Сделаю скидку на твою оторванность от реального мира.
Маняматику в школе учат не для того чтобы ты потом считал сумму ряда логарифма, а для того чтобы в мозгу в период развития организма образовалось как можно больше связей между нейронами. Это повысит уровень целостности нейронной сети и позволит думать/мыслить на более качественном уровне. Ведь если один нейрон связан с как можно большим числом остальных, в идеале о всеми, это позволяет проводить охуительное распараллеливание мышления и позволит прыгая на одной ноге пропукать подмышкой гимн британии, пропеть марш авиаторов одновременно дирижируя хором поющим dies irae и считая в уме при этом функцию комплексного переменного.
Но покалеченный топологией человек этого не поймет. Он только поймет что я плохо про топологию сказал и разорвется на сепарабельное пространство ровнехонько по эпсилон сети.
Первое, то что изучается в школе либо не нужно, либо это можно выучить гораздо быстрей. В школе квадратные уравнения с 8 по 11 решают. Тригонометрию полгода изучают, а затем синусы(икс) подставляют вместо икс в квадратные уравнения до конца обучения.
В ВУЗах, кстати, та же ситуация. Только вместо квадратных уравнений здесь интегралы. Преподы говорят, что это якобы улучшает понимание. Но как выпускник школы не знает, откуда взялся дискриминант и почему формулы корней кв. уравнения именно такие, так и выпускник ВУЗаесли это не ВШЭ или НМУнавряд ли в состоянии доказать теорему Ньютона-Лейбница, хотя 4-5лет её использовал, решая в неделю 100интегралов.
>Геометрия вот нужна для умения логически обосновывать свое мнение
Да? Может ты тогда покажешь мне логическое обоснование этого утверждения?
Эх.
По порядку.
Да, в школе все изучают медленно, конечно, совсем не так и не то, как ты описал, но медленно. Как из этого следует, что надо вообще перестать всех учить я не понимаю. Предлагаешь у бомжей последнее тряпье отобрать, нормальной одежды то у них нет?
Насчет формулы НЛ задел за живое, потому, что я понятия не имею, как она выводится, разве что в общих чертах.
В тех вузах готовят инженегров или еще кого похлеще, а не математиков, а даже если и готовят математиков, то не тех, которые в науке останутся.
Насчет геометрии я, разумеется откажусь от твоего предложения, а то сейчас начнется срач и цепляние к словам, требование объяснить, что значит слово "что" и прочее. могу лишь сказать, что знаю огромное количество примеров, подтверждающих мои слова. Хотя может геометрия не развивает, а лишь является следствием ума.
Есть какой-то науч-поп по математическим доказательствам? Просто не могу всё это уместить в своей голове и для меня всё это похоже на какие-то махинации непонятно как дающие результат.
Есть таблетка, ее пьешь и как Нео в мартице, все знаешь.
Для прокачки ума надо учить теорию множеств.
>Но покалеченный топологией человек этого не поймет
Забиваем в компьютер последовательность первых н простых чисел и говорим ему искать формулу по которой их нашли. Он выводит формулу, по ней ищем и проверяем слеующие числа.
Почему так еще не сделали?
Теория множеств
а) логичнее
б) абстрактнее
в) полезнее
элементарной геометрии.
А зачем?
Действительно, все гениальное - просто. Бегом беги патентуй и зарабатывай миллионы, только в интервью каком-нибудь не забудь упомянуть нас.
Ну а если серьезно, то я намекну, где ты ошибся.
>говорим ему искать формулу
Это предлагается в школе учить теорию множеств? Дети не могут понять, что два треугоьника равны, когда у них равны две стороны и угол между ними, а ты предлагаеь им узнать про то, что бесконечности оказывается разные бывают?
>два треугоьника равны, когда у них равны две стороны и угол между ними
Доказать это невозможно (аксиома), это предлагается зазубрить. Нахрена.
Лучше изучать простые и понятные диаграммы Эйлера-Венна.
У кого аксиома, а у кого и не аксиома, это раз. Два это то, что это в общем-то очевидный факт.
Дело то еще вот в чем. Элементарной теории множеств хватит не на долго, а не элементарную дети учить откажутся. Первая, кстати, в какой-то мере изучается в школе.
Бессмысленный и беспощадный. Я не вижу причин изучать следствия из этой аксиомы, попробуй убедить меня.
Её вполне достаточно, чтобы без натягов заполнить весь объём времени, отведенный на геометрию.
> Я не вижу причин изучать следствия из этой аксиомы
Ок
>попробуй убедить меня
???
>Её вполне достаточно, чтобы без натягов заполнить весь объём времени, отведенный на геометрию.
Видимо я слишком мало изучал теорию множеств, раз не могу придумать что-то еще, что могут изучить школьники кроме диаграм и простейших операций. Задач тоже, особо много не придумаешь. А я напоминаю, что геометрия изучается с 7 по 11 класс. И это только как отдельный предмет. К тому же, если говорить, о математиках, то им часто нужна простейшая геометрия, к которой однако нужно привыкнуть.
Например, подобия быстро не расскажешь, а вот канторов диагональный метод, который, вообще говоря, не стоит показывать школьникам, - запросто.
На английском много всего.
7 класс - определение множества, диаграммы Эйлера, основные отношения и операции, формула включений-исключений, формулы де Моргана.
8 класс - определение функции. Биекции, мощность множества, счетные множества и теоремы о них, теорема Кантора о булеане, характеристические функции, несчетность R.
9 класс - теорема Кантора-Бернштейна, кардинальная арифметика. Отношения, чумы.
10 класс - лемма Цорна и её следствия. Ординалы, трансфинитная индукция (с упором на индукцию по конечным ординалам).
11 класс - ZFC, NBG, MK, универсумы V и L. Структуры и морфизмы.
Так блядь, серьезный математический вопрос наконец то созрел.
Почему декарт вставлен в мануал hdoom-а? В чем скрытый смысол?
Когета ерга зум.
А порномод то тут при чем?
Он вывел из этого теорию универсальной любви.
Чего чего?
Явно мало. Хотя если учесть сколько нужно будет топтаться на месте, чтобы дети привыкли, года может будет и мало.
Помню в 9 классе нас нормально порвало на диагональном процессе. А мы были мат школьниками, которых обучали по спец методикам хорошие педагоги. Что будет, когда марьивановна в мухосранске в 8 классе скажет, что рациональных чисел столько же сколько и натуральных, я думать не хочу.
Вполне школьные темы. А элементарная геометрия не нужна, желающие смогут самостоятельно изучить все необходимое.
>желающие смогут самостоятельно изучить все необходимое
Древние греки значит были не желающими изучать все самостоятельно, раз ждали пока эвклид придет и пояснит им все.
>НЛ задел за живое, потому, что я понятия не имею, как она выводится, разве что в общих чертах
Там 2 строчки. Можешь в Фихтенгольце прочесть. Хороший, кстати, учебник, если читать выборочно. Я про двухтомник. Отлично и понятно написан, читать его можно в классе 5ом.
>Как из этого следует, что надо вообще перестать всех учить я не понимаю
Первое, это учат плохо. Второе, даже если бы учили хорошо, то большинству это не нужно. Поэтому лучше никак не учить. Представь, если бы тебя в школе заставляли учить какое-нибудь римское право. Ты скорее всего учился бы на 3, а после выпуска всё бы забыл. Вот так же и у тех кому это право нравится с математикой. Также по этой же причине нужно отменить химии физики... Кому нужно будет сам выучит. Вот Карина хорошо пояснила https://www.youtube.com/watch?v=FZ9tivf63Y4.
Доказать можно все 3 признака равенства. Если взять за аксиому, что треугольники равны, если у них все стороны и углы между собой равны и использовать синусы-косинусы, то можно прийти к теореме синусов и косинусов.
Смешно. Это нахуй никому не надо, дальше формул де Моргана никто не зайдет.
>7 класс - определение множества, диаграммы Эйлера, основные отношения и операции, формула включений-исключений, формулы де Моргана.
То что читается за 10минут ты предлагаешь растянуть на год.
>ты предлагаешь растянуть на год
Элементарную геометрию же растянули, и ни у кого из её фанатов вопросов не возникает.
Представил себе задачники по теории множеств, где тысячи заданий вида: найти пересечение {0,1,2,a,b} и {0,a,c} или выписать все подмножества {0,1,2,3}. И так на протяжении года.
Не нужно никого этим учить, кто захочет сам выучит.
Тогда логичнее целиком отменить среднюю школу.
Давай уже определимся чего ты хочешь получить от образования школьного.
Те, кому нужно могут и математику всю выучить и вообще что угодно.
адекват, но мне плохо от матана становится
посмотри программу за 7 класс и посмотри на количество задач в учебнике атанасяна к прмеру. И я повторяю, что все это нужно для обучения математиков потом и материала там очень много. А те, кому математика в удущем не понадобится просто учятся логически мыслить.
Да. Обеими руками ЗА!
Видел где-то лекцию тетки педагога из Питера, где она объясняла, почему нелья учить читать по слогам и какой смысл во всех этих биологиях химиях математиках в школе.
>что все это нужно для обучения математиков потом
Ой, лол. Ну кому ты пиздишь.
Там задачи однотипные. Лучше давать школоте доказывать теоремы. Если не рассматривать слишком извращенные теоремы, типа теоремы принцессы Елизаветы, то элементарную геометрию можно освоить за год, а то и меньше.
тащи видос.
Геометрия нужна в том же матане.
Нет причин её осваивать.
Лол ещё раз. Ты серьёзно?
Если только ей и занмиматься и если у тебя за плечами несколько курсов какого-ниубдь жесткого универа, то да, можно освоить. Что значит однотипные задачи тоже не понятно, вон глянь геометрию в ЕГЭ, как-то не особо они похожи друг на друга. Доказывать теоремы, конечно, это отличная идея, меня учили именно так, но обычная школота не потянет подобное.
Не могу вспомнить кто и когда. Вот надеюсь, что анон знает о чем я.
>глянь геометрию в ЕГЭ
Это единственное место, где используется школьная "геометрия". ЕГЭ.
Ой бля, да хватит доебываться. ЕГЭ проверяет все, что ты должен знать за курс школы и разнообразие задач в нем показывает, что и геометрия это огромный пласт материала.
Ну а если мне не верят, что в матане много элементарной геометрии, то я и не знаю что сказать.
>в матане много элементарной геометрии
Чувак, ты всё-таки в /math. Тут некоторые люди учебники матана, ты не поверишь, читали.
Как это противоречит моим словам?
Ты врёшь.
Не буду отрицать, меня хлебом не корми, дай напиздеть.
Как ты представляешь себе элементарную геометрию в матане?
часто возникает такая ситуация, смотрим мы на график какой-нибудь или решаем дифур и тут фраза, рассмотрим два треугольника, они равны по тому-то тому-то.
Честно скажу, не могу вспомнить какие именно теоремы и когда так доказываются, но то, что во время моего не очень напряжного обучения я часто слышал подобное, это точно.
>но обычная школота не потянет подобное
Именно поэтому нужно отменить нахуй.
Ща гляну. Пиццу закажу как раз.
>они равны по тому-то тому-то
возможно. но тебе навряд ли встретиться задача, где нужно будет проводить биссектрисы и использовать какую-нибудь теорему для неё. Говорю же, геометрия не бесполезная вещь, но большинство теорем в ней, изучаемых в школе, довольно экзотичны.
Да тебе волю дай, ты бы всех сжигал, кто не знает интегрирования по частям.
Школа нужна не для того, чтобы готовить математиков, а для того, чтобы выпускать адекватных, сформировавшихся личностей, которые имеют знания о мире и способны думать своей головой.
Да, тут ты прав. Но никто не говорил, что все это потребуется.
Похож на извращенца
Мда уж. Теоремы стоит доказывать и это мое больное место. Как-то на уроках геометрии говорили мол, "Времени мало. доказательство приводить я не буду, вы сами там почитайте, порешайте, научитесь". Потом еще и пропускал и потом лишь слушал "а вот тут мы применим теорему косинусов... Смотрите дети, можно заменить sin [уравнение] на cos [другое уравнение] Зачем? Ну, вы там короче перепишите табличку тригонометрических уравнений и всё. О, хотите покажу как умножить число на 11?? ААА, хотите? ... А я люблю геометрию ибо там просто символы переставляешь". Так и закончил 9 класс не умея доказывать простейшие теоремы, лишь помня отдельные факты, а зачем нужна теорема косинусов узнал преимущественно отсюда. Так и вырос бестолковщиной, в последнее время правда научился более-менее в элементарную теорию множеств, комбинаторику и арифметику, что вообще где-то уровень 7 класса, даже меньше. Ну, и алгебры чуть, но тоже пока фактами, впрочем, замечаю что геометрия там бы явно помогла, так и решил ее привести в порядок и доказательство теорем.
Вот есть даже элементарная теорема, которую надо доказать и более того, даже указание к ней. Можно интуитивно отрывками что-то мямлить о том, что можешь взять любую из точек и эээ, она... ээээ.... что и надо доказать, а ты принимаешь это как очевидное. А ведь надо рассуждать, ибо можно очевидно начертить и всякую дребедень, которой нет. И чувствуешь себя тупым.
Хотя можешь я один такой несообразительный, вроде и с мозгом особенности какие-то, но это же элементарно ведь.
Но ведь интригалы это математический спид.
Решил один иноргал - зашкварился на всю жизнь.
Тем более что чуть более чем все местные топологи не могут не то что интеграл, дифференциальное уравнение решить не могут. Ящик тому примером.
Мысли, про то что ты глупее других отгоняй. В каких-то задачах ты преуспеешь, в каких-то будешь тупить на элементарном. Все по разному мыслят. Главное чтобы тебе было это интересно.
Уже и сюда свой срач приплелт, долбоебы. Тригерится на слово интеграл это уже совсем пиздец.
Обожаю решать площади под кривой интегралами
x^6=-13 Найти все корни уравнения.
Как их искать то?
Ты так говоришь будто нужно обязательно рядами искать площади.
Формула Муавра
Занятное видео. Не со всем согласен, но суть того что она пыталась донести мне знакома. Учат образам, а не сути понятий/вещей. Цифрами и позиционной системой записи чисел образы чисел заменяют сами числа, картофаном с водовкой саму суть интегрирования как суммирования бесконечно малых, деньгами измеряют успех.
Короче эдакая аналогия пещеры платона.
>Формула Муавра
Попроще есть способ.
Я собираюсь написать основную теорему алгебры о корнях равных по количеству значению степени, но только так чтобы даже конченый дебил понял.
>Я собираюсь написать основную теорему алгебры о корнях равных по количеству значению степени
теорема безу
теорема безу + "дама с собачкой".
быстрофикс
Прикольная задача, я вроде решил. Пикрелейтед математическое решение и прогу еще написал, чтобы проверить:
https://ideone.com/4BRj12
Тред не читал. Посоветуйте учебник/справочник со всеми свойствами и формулами логарифмов, пределов, производных, первообразных, тригонометрических функций, etc.
Обязательно с доказательствами, конечно.
Обязательно с доказательствами, конечно.
Анон, поясни, пожалуйста, откуда взялась j-я производная на пикрелейтед.
Точнее не так, это я понял, я не понял, что значит "applying directional directional derivative j times to f". Частная производная - это же число, не? То есть больше 1 раза мы ее не можем применить. А формула у меня получилась
g'(t) = sum hijdjf/dxij, где x = a + th.
Бля, чет формула не очень написалась.
Лол, опять не то написал.
в какой программе пишешь?
А ты умеешь приводить доказательства так чтобы даже конченный дебил понял?
Короче, это все неверно. Должно че-то другое получиться, но я не могу понять как.
Их и так в школе изучают, на информатике.
Равномощность натуральных и рациональных чисел объясняется в 9-10 классе.
Нихуя там не объясняют.
А раз такой умный, скажи, каких чисел больше рациональных или иррациональных?
Опять ты?
иррациональных
Пруф, маня.
Арнольдач, есть какие-нибудь книги по основным численным методам с реализацией на каком нибудь языке, желательно псевдокоде. То есть упор идет не теорию, а именно на реализацию, что и как лучше делать и тп.
Епт, четыре года я на этой пораше и тут до сих пор н определить не могут. Что с вами не так?
Берешь код какой-нибудь опенсорсной библиотеки и читаешь. Вот, к примеру
https://github.com/numpy/numpy
нахер мне нумпай, тем более в си говне разбираться. Там нет чо как и почему
Это не учитывая того что там основных численных методов нет.
Каждое рациональное число ответвляется на кучу иррациональных (если мы говорим о предельных числах) путём сложения, умножения и т.п.
Ты аутист? Ты написал
> упор идет не теорию, а именно на реализацию, что и как лучше делать и тп.
То есть, не хочешь знать теорию - берешь и разбираешься в реализации. Как там реализовано, так и лучше делать по мнению авторов библиотеки. Хочешь какой-то конкретный метод - просто в гугле вбиваешь и найдешь кучу реализаций с псевдокодом.
>си говне
Справедливости ради, ничего лучше не придумали за 40 с лишним лет.
Все, отбой, разобрался.
Еще есть фортран для самых упоротых.
А для вконец отмороженых сосачи.
И чо?
После изучения исчисление предикатов можно ли будет сказать, что я понимаю логику как нормальный человек с нормальным интеллектом. Достаточно ли этого? Ну, и посоветуйте книги тогда уж, пожалуйста.
Блять, как быть с бесконечностями?
Для меня бесконечность это алгоритм следуя которому можно повторять этот алгоритм сколько угодно раз и не исчерпать возможности алгоритма.
Например прямые это линии которые обязаны продолжаться если мы достигнем их конца. С числами можно добавлять один/умножать на число больше одного и получить неограниченно большое число и т.д.
Как с таким подходом находить пределы и площади под кривыми? Считать тупо в лоб сперва десять, потом сто, потом стотыщмильеннов а там где то рядом и стопицот с числом гремма?
Или я как то неправильно понимаю бесконечность?
Смотри дед! Конструктивист растет!
Нет, после изучения предикатов, ты будешь знать исчисление предикатов и все. Чтобы понимать логику как нормальный человек нужно закончить школу.
Чтобы понять площадь под графиком нужно посчитать сумму для конкретного разбиения, а потом взять предел, у которого есть вполне конкретное эпсило-дельта определение.
Каким образом решать степенную функцию? Например, дана функция y=x^7, а надо чертить. Мне подставлять числа 1,2,3? Тогда как мне надо график растянуть, блять?
Лучше для чего? Для научных вычислений? Вместо решения задачи, ты пердолишься с памятью на си, великолепный язык, лучше не придумали просто. Тот же фортран даст пососать си в скорости и с десяток других в удобстве написания и либах.
АНАНАСЫ, почему ответ не 9?
1.проинтегрировал -2x^2 + 3x + 5 от -1 до 2, получилась площадь S1=13.5
2.нашел площадь S2=4.5 под прямой
S1-S2=9, то есть искомая площадь, но нихуя.
что я сделал не так?
1.проинтегрировал -2x^2 + 3x + 5 от -1 до 2, получилась площадь S1=13.5
2.нашел площадь S2=4.5 под прямой
S1-S2=9, то есть искомая площадь, но нихуя.
что я сделал не так?
Да вроде 9 правильно
либо мы одинаково тупим
Не понял тебя. Это ты меня так оскорбил или что?
Я и так понимаю суть площади по кривой. Разбитие её, площади, на охулион прямоугольничков-трапеций, чтобы сделать бесконечно малой погрешность, и потом суммирование этих самых охуллионов прямоугольничков.
Ты мне про бесконечности объясни.
Считаешь функцию с шагом в 1-0.5 и соединяешь получившиеся точки отрезками, получаешь примерный вид кривой.
>почему ответ не 9?
Автор этого задания объебался водярой и опечатался.
>чтобы сделать бесконечно малой погрешность
Я боюсь это не вся суть определения, стоит таки выучить его через пределы.
С бесконечность тоже, все довольно просто. Есть у тебя множества в которой есть 1 и если есть n, то есть и n+1.
Как не вся? Объясни где ошибка? Я же написал то как понял суть интегрирования.
Ну так и как я с таким определением бесконечности буду искать пределы и находить площади под кривыми?
Я не могу указать где ошибка в твоем определении, потому что это не определение. Но грубо говоря, тебе кажется, что интегрировать можно любую кривую. А это не так.
И что в моем определении мешает тебе искать пределы? В определении предела,вроде как, даже слово бесконечность не встречается.
Аргумент стремится к пределу целую бесконечность.
Давай тогда книжку прочитав которую у меня пропадут все вопросы.
И да, интегрировать можно практически любую, даже если она обрывается, но на обрыве не уходит в бесконечность. Как плавление льда. Энергия проебывается, температура не меняется, график терпи разрыв, чтоы потом, после смены агрегатного состояния всего куска льда пошел дальнейший рост температуры.
>стремится
Это как?
>к пределу
Определяешь предел через предел?
>бесконечность
>целую бесконечность
Есть нецелые? И к какой конкретно бесконечности стремится?
А поможет тебе любой известный вводный учебник по матану. Какой конкретно не скажу, на меня выльют помои за уодно только упоминание Зорича или Камынина.
Ряды тоже преследуют цели интегралов, просто другими методами. В итоге же число что от ряда что от интеграла будет одним и тем же.
Последовательно проходит все допустимые численные значения, но не становится числом к которому стремится, если при таком значении функция теряет смысл.
>Зорича или Камынина
Щас бы водовки да картофанчиком закусить...
Началось бля. только не в жопу.
Ты это к чему?
Тот же вопрос.
Если вкатываетесь, то вкатывайтесь по цельной программе и полноцено.
Си - одна из худших вещей, случившихся с современным миром.
>ООП - одна из худших вещей, случившихся с современным миром.
Ну, да, но это вроде бы уже даже последнему колхознику очевидно - в отличие от.
Есть же няшное реактивное программирование, которые покрывает ООП и красиво (и просто, да) описывается математически. Но зачем это тут обсуждать?
Но ведь цельных программ нету. Есть только отдельно алгебра, отдельно геометрия отдельно вышмат.
>теорема безу
Теорема Безу утверждает, что остаток от деления многочлена P(x) на двучлен (x-a) равен P(a).
P=11
X=3
A=1
113/3-1=33/2=16(остат 1)
P(a)111=11
Респект таким доказанным теоремам.
Нужно делить на двучлен (х-1).
P(x) = 11;
a = 1;
11/(x-1) остаток 11. P(1) = 11.
А как у тебя вышел остаток 11, при делении 11/10? Очень интересно узнать мнение эксперта.
Болит голова от математики, притом, что решаю элементарные задачи.
Как с этим справляться?
Как с этим справляться?
ВОПРОС:
Есть функциональный ряд, то есть каждый его член - функция от переменной игрек.
Сходится он при -1<y<+1.
Посчитал я сумму ряда для каждого такого y.
После - проинтегрировал этот результат по dy от 0 до x.
Вопрос - какому множеству должен принадлежать икс, чтобы интеграл существовал?
Есть ряд, sum( fn(x) , n e N ) .
Я тебя не понимаю. Я делил 11 на (х-1), откуда 10?
Остаток 11 получился, потому что 11 = (x-1)·0 + 11
В твоём примере у тебя многочлен P(x) = 11, то есть при любом x: P(x) = 11. Поэтому P(3) = 11, а не 11·3. В знаменателе ты делишь на одночлен 3-1 = 2. А нужно на двучлен.
Многочлены, как и числа, можно делить друг на друга с остатком. P(x) = (x-a)Q(x)+ост. Если подставить вместо икса а, то P(a) = 0·Q(x)+ост = ост.
Подышать воздухом свежим, прогуляться. Отвлечь свой "вычислительный контур" мозга на что-то более расслабляющее, потом снова вернуться к решению задач.
Гайз, почему у данной доски еще нет (или есть?) своя конфа в телеграмме? Почему, в конце-то концов, Рыбников устраивает стримы своего пиздеца в интернете, а здешние аспиранты/кандидаты не проводят обучающие онлайн семинары?
Вредная, плохая, глупая идея.
Даже сходки лучше этой идеи.
На дваче половина народа - сычи. А вот популярных лекций с разъяснениями трудных для понимания тем очень не хватает. Желательно с ответами на вопросы в прямом эфире.
>Рыбников устраивает стримы своего пиздеца в интернете
Как будет стрим, скинь ссылку.
>своя конфа в телеграмме
Пошли от сюда на хуй, хипстеры. Есть вопросы пиши мыло, или индекс с адресом.
>здешние аспиранты/кандидаты не проводят обучающие онлайн семинары?
Зачем, если этого и так дохуя и больше. Это если простое. Если сложное, то будет 2 зрителя. Пустая трата времени.
двачую, в какой программе это пишется?
Сап. Не знаю, куда лучше с таким вопросом идти, поэтому я здесь. Заканчиваю 2 курс прикладной математики и информатики. Чудом не вылетел. За 4 семака множество пробелов и хотелось бы как-то наверстать, дабы с 3 курса уже начать нормально учиться.
Посоветуйте годноты (глубже, чем матпрофи) по следующим предметам:
Матан (до рядов более-менее знаю, дальше - 0) + тфкп теория функции комплексного переменного
Дисмат (Сюда же матлог и теорию графов)
Линейная алгебра (вроде так называется, там матрицы еще)
Дифференциальные уравнения
Тервер
Ну и конечно всё это не на уровне заочника, а на более приличном хотелось бы знать.
Спасибо заранее, надеюсь не обоссыте и не оставите в беде.
Посоветуйте годноты (глубже, чем матпрофи) по следующим предметам:
Матан (до рядов более-менее знаю, дальше - 0) + тфкп теория функции комплексного переменного
Дисмат (Сюда же матлог и теорию графов)
Линейная алгебра (вроде так называется, там матрицы еще)
Дифференциальные уравнения
Тервер
Ну и конечно всё это не на уровне заочника, а на более приличном хотелось бы знать.
Спасибо заранее, надеюсь не обоссыте и не оставите в беде.
Отличный бизнес план - математические стримы. Вот ты этим и займись.
Письменный, Конспект лекций по высшей математике.
Демидович, Краткий курс высшей математики.
Андерсон, Дискретная математика и комбинаторика.
Гнеденко, Элементарное введение в теорию вероятностей.
Но там есть опечатки, например у Письменного в одном из изданий неправильно выводится экспонента, а у Андерсона на стр. 103 ужасающе неправильно определено отношение частичного порядка. Сверяйся с википедией.
Хорошо, спасибо. А практика? Какие задачники предпочтительнее? Вообще по дисмату у нас в почете учебник Тишина например, но что-то как-то не знаю.
Я плохо разбираюсь в задачниках, мне-то хватает листочков и упражнений из книг.
Потому что тут могут только инъектировать в одно место друг другу.
>надеюсь не обоссыте и не оставите в беде
Оставим. Иди на хуй. В сети есть сотни списков, как и в шапке треда, так и на форумах и бложиках.
На самом деле прибыльно, сейчас школота дрочит на НОУКУнаучпоп. Хотя они физикобыдло и наверняка будут задаваться вопросом нахуя это нужно в хуизике.
Шарифов вон поясняет что такое предел последовательности и как решить неравенство, гребя бабло с партнерки.
>физикобыдло и наверняка будут задаваться вопросом нахуя это нужно в хуизике
И тут из за угла в машине со сваг-стилем под маткор выезжают успешные математики с кучей денег, пафоса и шлюх.
Даже если мы будем играть во все эти лимонные игры с многочленами. И ДАЖЕ если мы возьмем твой пример.
Как ты узнал что (x-a) =0? при делении на ноль выражение смысла автоматически не имеет. И почему я в двучлене не могу задать отдельные переменные, мне как-то тоже не очень понятно.
Сам то как думаешь, кто-то из обывателей согласится заниматься таким говном, чтобы понтануться?
А теперь обоснуйте, почему в ГДЗ написана какая-то чушь а не эту очевидная формула с пикрилейтед.
Только не говорите что я эту часть 2 раза приплюсовал этой формулой...
Вот, вообщем это формула, ну точно должна подходить, хотя в ответе энивей другая. Подставил переменные в формулу из ГДЗ и в эту - не подходит.
Эта фигура называется "гномон".
XxM+NxY-YxM
Показывали только что по ящику историю создания какой то там китайской башни гуаночжоу. Она на фото.
Так вот, там говорилось что из за того что башня имеет гиперболическую форму она прочнее точно такой же башни, но если бы её построили как обычный цилиндр.
Там еще говорилось что то про конические сечения, про то что можно было еще уже сделать "шейку" башни сэкономить и получить сравнимую прочность.
Это вообще как?
Ты заебал. Многочлен можно выразить через другие. P(x)=R(x)Q(x)+остаток.
Есть многочлен P(x), выразим его через (x-a), где a - какое-то число. P(x)=(x-a)Q(x)+остаток. Подставим P(a)=(a-a)Q(x)+остаток=0Q(x)+остаток=остаток.
>Как ты узнал что (x-a) =0
(x-a)!=0
>при делении на ноль выражение смысла автоматически не имеет
Делят P(x) на (x-a), а не на 0. Если тебя смущает 0 при x=a, то если 4 поделить на 5: 4=0·5+4
>И почему я в двучлене не могу задать отдельные переменные, мне как-то тоже не очень понятно
Потому что в твоей замене [3-1=2] получается число. Ты многочлен делишь на число, а нужно на многочлен. Когда ты уже поделил, то можешь подставлять какой угодно x, но цель найти остаток, поэтому на место x нужно поставить a.
>Подставим P(a)=(a-a)Q(x)+остаток=0Q(x)+остаток=остаток.
P(a)=(a-a)Q(a)+остаток=0Q(a)+остаток
fix
Ну же, Анон! вопрос - тут:
Ряды какие-то. Это картофан походу. Не хотят решать анончики. Смирись. Или добавь пучков.
Стоит изучить курс аналитической геометрии.
Ты просто задал вопрос, для которого нужно знать не очень популярную теорему, но она точно есть в теме интегрирование рядов.
Книжку давай
Александров, курс аналетической геометрии.
Ну да. У задачки очевидно есть решение. Зачем её решать если решение есть?
Там точно про это пояснят?
Когда я читал, поясняли.
>Сходится он при -1<y<+1.
Вроде если нет равномерной сходимости, то ничего там интегрировать нельзя.
даже если границы интеграла не выходят за пределы от -1 до +1 ?
>если границы интеграла
Это тут совсем непричём. Если нет равномерной сходимости ряда на данном множестве, то ни о каких дифференцирования/интегрированиях этого ряда речи идти не может.
Что не так с этой формулой? Можно конкретеки?
Как составить уравнение для данной функции? С английским не особо дружу, но похоже, что тут сверхлинейная зависимость.
Математика изучает только количество по своей сути?
Странный вопрос.
Нет
S=xm+yn-xy
Так получают количества и отдают количество, разве нет? И преобразования над количествами, ну это к основаниям но то неинтересно.
Я не понимаю, что ты спрашиваешь и какими словами оперируешь. А самое главное, зачем оно тебе надо.
Чем отличается вектор от графа?
Вектор - точка модуля над полем, а граф - объект категории графов.
Аноны, реквестирую формулу, которая позволяет рассчитывать радиус для описанной вокруг многоугольника окружности с учетом того, что длины сторон одинаковые.
Многоугольник, само собой, равносторонний. Нужно, чтобы длина одной стороны при любом радиусе была одинаковой.
Вектор это стрелочка в пространстве, а граф это нечто что имеет какую то определенную связь с какими то другими вещами.
Если многоугольник с нечетным количеством углов опускаешь из двех углов вершины, находишь точки их пересечения, находишь расстояние от этой точки до какого то угла.
Если четное число сторон, проводишь диагонали и от точки их пересечения находишь расстояние до любого угла многогольника
Нет, ты не понял. Вот есть n-угольник с радиусом, например, 300, у него длина стороны, например, 5. Мы строим n+1-угольник рядом. Какой необходимо задать радиус, чтобы длина стороны осталась 5?
Тебе это надо?
Короче, Ri = R(i-1)*(sin(180/n)/sin(180/n+1)). Верно?
Да
ПУЧК!
Вектор - направленный отрезок, граф - несколько точек, соеденные отрезками.
Почему 3abc обозначает abc+abc+abc, а не, например, a+a+a+b+c?
Гугли умножение.
Потому что там написано 3 a b * c
(3a)bc=(a+a+a)bc=abc+abc+abc.
О, етить! То что нужно! Наконец-то понял. Восхитительно.
Хотя может отдохнуть надо.
Наверно, правильнее написать в этот тред:
Как генерировать матрицы с высоким числом обусловленности?
На каких ещё матрицах тестировать алгоритм, решающий системы линейных уравнений?
Как генерировать матрицы с высоким числом обусловленности?
На каких ещё матрицах тестировать алгоритм, решающий системы линейных уравнений?
>Вектор - направленный отрезок
Не, нихуя. Вектор - это класс всех направленных отрезков, совмещающихся каким-нибудь параллельным переносом.
Кстати забыл, в какой книге это написано в начале? Там перед этим о равенстве векторов через параллелограмм.
Читаю вот эту хуйню
https://www.math.wisc.edu/~keisler/calc.html
Занятное чтиво. Собственно, из за таких вот оснований маняматики друг друга в говны тычут и толстеннымы талмудами по ебалам бьют?
Чем так нестандартный анализ не нравится? Или он тут не такой который должен быть? Или причина в том что в нестандартный анализ топологий не завезли?
https://www.math.wisc.edu/~keisler/calc.html
Занятное чтиво. Собственно, из за таких вот оснований маняматики друг друга в говны тычут и толстеннымы талмудами по ебалам бьют?
Чем так нестандартный анализ не нравится? Или он тут не такой который должен быть? Или причина в том что в нестандартный анализ топологий не завезли?
>Чем так нестандартный анализ не нравится?
Потому что он не даёт никаких новых теорем, которые нельзя получить в классическом.
В наши дни нормальные математики такой ерундой не занимаются, если что. Дрочить "основания" - удел импотентов, которые физически не могут заниматься чем-нибудь действительно интересным.
Александров.
В кубе 6 граней, но всегда будет 3 ребра?
Так ты и не можешь делить не на (x-a), ни на (x-1) не задав эти вонючие переменные. Что я читаю? Опять таблетки забыл принять?
Архив тредов протух
>не даёт никаких новых теорем
Педивикия говорит что ты пидор.
Значит в треде про основания, про классицизм интуицизм, формалист, харкачизм, сидят одни отбросы, которые ящик посчитать не могут и с трудом два плюс два складывают?
у вас ящик головного мозга
вы всё что читаете понимаете как ящик
ящик
Делят на (x-a), где a - какое-то число.
Многочлены можно делить.
А вообще ты заебал. Иди на хуй, зелень.
>Педивикия говорит что ты пидор.
Ты невнимательно её читаешь. Все результаты нестандартного анализа можно получить и в классическом.
>Значит в треде про основания, про классицизм интуицизм, формалист, харкачизм, сидят одни отбросы, которые ящик посчитать не могут и с трудом два плюс два складывают?
Да
анчаусы, посоветуйте, что посмотреть и порешать по обратным тригонометрическим функциям. А то у меня в интегралах получается, что-то типа arctg( 2tgx) и хз как все это упрощать.
Ты физически не сможешь найти остаток не задав переменную x, ты что в детском саду вообще? Там нету равенства. Иди нахуй, обзывается ещё на людей.
Помогите. Ребро же это вот это? Там больше 3 не может быть.
>arctg( 2tgx)
дуга тангенс которой равен двум тангенсам икс, что тут не понятного?
Но ведь там написано что в нестандартном анализе все тоньше объясняется.
Нет, это вершина. У куба 6 граней, 8 вершин и 12 ребер.
Сап, анон-математики. Я школьник, поэтому сильно не бейте. Лучше подскажите, как прорешать данное уравнение и куда нужно копать.
(1/6)^5x-16 - 6 <= 0
(1/6)^5x-16 - 6 <= 0
(1/6)^(5x-16)-6<=0
фикс
Ло гарифм
Значение знаешь?
>>21853
>21854
Это степень, которая получается между основанем логарифма и заданным числом.
То есть.
log1/6(5x-16) - log6(1) <=0
Если не накосячил, конечно. Но что нужно дальше?
На репетитора денег нет, а училка огрызается.
Есть какие-нибудь годные задачники по матанализу с решениями, кроме Виноградовой и Антидемидовича? Посложнее че нить
Точно. Про эту годноту я и забыл
+ отработать гиперболические функции, а то я их боюсь
Щас поишу тебе книжку.
Обратные тригонометрические функции С.И.Новоселов
Янпольский А.Р. - Гиперболические функции
Вот это годнотень. Спасибо за обе!
Переведи все логарифмы на одно основание чтобы работать можно было с ними.
Не протух, просто ты послан нахуй
Это ты вектор с ориентированным графом перепутал что ли? хуя малец
гугли все по отдельности, зачем такими вопросами засирать и без того обосранный тред
Обычный лист бумаги держит ручку.
С точки зрения механики сплошных четвергов я таким изгибом делаю в бумажке ребро жесткости.
Поясните мне с точки зрения математики почему ребро жесткости собственно дает жесткость?
Слишком сложно. Поясни понятнее, пожалуйста.
Такой вопрос специфический: кто-нибудь пробовал с математическим (ну или околотехническим) образованием перекатиться в финансы? Можете entry-level что-нибудь посоветовать по рынкам для математического ума.
Можно получить человеческое объяснение, как найти x из данной позиции?
Это не уравнение - твоё выражение ничему не приравнено. Поэтому ничего тут найти нельзя. Умри.
Смысла мало. Финансы работают не по математическим законам. Закономерности конечно есть, но они работают только на десятилетних периодах минимум.
Ребята, вы не видели Пыню? Он вчера ушел, сказал за учебником Серра, и не вернулся.
Этого маню удаляем и не слушаем. Матмоделирование, методы оптимизации, оценка рисков, машобчик -- вот это все вперемешку применяется и хорошо работает. Если ты про "экономиста" из шараги, который не знает математику, то да.
Уже тысячу раз пояснили, что это маняфантазии, что если бы это работало, то были бы фрилансеры 300к/c на наяву. Предсказать никак нельзя, поэтому никого безумно богатого нет.
>Если ты про "экономиста" из шараги, который не знает математику, то да.
Все "норм" экономисты сидят и рулят чужими деньгами, получая 100к зп в эрэфии.
https://ocw.mit.edu/courses/mathematics/18-s096-topics-in-mathematics-with-applications-in-finance-fall-2013/
https://ocw.mit.edu/courses/sloan-school-of-management/15-401-finance-theory-i-fall-2008/
https://ocw.mit.edu/courses/sloan-school-of-management/15-450-analytics-of-finance-fall-2010/
Из математики почитай линейную алгебру (Акслер например), анализ (Зорич там или Рудин), диффуры (Арнольд), введение в теорию меры (Терри Тао), теорию вероятности (Ширяев, Вероятность-1 и -2)
Этот лист довольно сильный оверкилл потому что формально достаточно только "вычислительных" курсов - калькулюса, линейки без особой теории, диффуров тоже без неё, но раз уж ты спрашиваешь на /math/ и про математическое образование, то я думаю этот список + MIT OCW в самый раз
И тут ты такой заглатываешь двухметровый хуй, потому что пояснить почему рокфеллеры с абрамовичами стали миллионерами которые из математики знали только что то уровня 2+2=5 ты не можешь.
>нефтяной магнат и другой нефтяной магнат не знали математику
ОК, но при чём же тут финансы?
С логикой вообще провал - существование людей которые разбогатели не зная математики не доказывает бесполезность математики (тем более кокретно для финансовой сферы), а только её крайнюю необязательность для цели обогащения. А то я тоже могу привести Джеймса Саймонса в пример и утверждать что все кто не знает математику заглатывают и никогда не смогут разбогатеть
Ну, я похоже понял тебя. Ты под финансами имеешь ввиду предсказание курса доллара на завтра с точностью больше 51%. Я под этим имею ввиду научную дисциплину, которая применяется на практике и сама использует сильный математический аппарат. Луркай
Ошибка выжившего, мазафака, ду ю спик ит?
И потом, раз все на маняматике держится, почему ты сосачируешь на мылруче, а не ебешь кайенских шлюх на коксовом острове где то посреди арабских миратов, предварительно натерев залупу и подзалупное пространство каким то псилоцибином, для остроты ощущений?
пиздец полнейший
>И потом, раз все на маняматике держится
С кем ты споришь, упоротый? Если тот с кем ты споришь делает такие утверждения, то на его посты и ссылайся, а не на мои.
И вообще связь "финансы=успешный миллиардер" она только в твоей тупой башке. Ты до людей интересующихся программированием тоже доёбываешься в стиле "хули ты не цукерберг?"
И что, и в трейдинге помогает не слиться?
>которая применяется на практике
Какой именно практике? Прогнозирование курса доллара?
Умрешь здесь тольк только ты мяняматик. Послал лучи рака легких в твои легкие, лол.
Так что отдыхай. Ты кстати, не избежишь этого, ты уже мертв как бы по факту. Умри.
Сильный математический аппарат, это ты про интеграл? Там нихуя нет.
>Я под этим имею ввиду научную дисциплину
и что же она изучает?
Беда то какая. В треде для начинающих многообразия над топологическими пространствами не дрочат. Бида бида...
Ты совсем уже ебнулся со своей ненавистью к алгебраистам или кому-то там, шизик.
2 Вопроса:
1. Почему правильный ответ - икс под номером 2? Ведь -2pi/3 лежит в III четверти, где sin < 0, а 2pi/3 - во II, где sin > 0.
2. Правильно ли я поставил скобки?
1. Почему правильный ответ - икс под номером 2? Ведь -2pi/3 лежит в III четверти, где sin < 0, а 2pi/3 - во II, где sin > 0.
2. Правильно ли я поставил скобки?
Да хули отклеилось то
Как все таки пнимать бесконечно малую? Я могу её представить как дробь 0.00...бесконечное количество нулей...1?
Ебать, в этом итт треде анон нашёл конец бесконечности
>Как все таки пнимать бесконечно малую?
Читать определения в учебниках анализа и не городить чушь.
>Почему правильный ответ - икс под номером 2?
Кто сказал?
Ну подставь 2pi/3 в исходное уравнение и удостоверься что тебя обманывают.
>Я могу её представить как дробь 0.00...бесконечное количество нулей...1?
Нет не можешь.
И мне вот интересно, откуда ты узнал о бесконечно малой и математике вообще? Просто интересно, откуда вы лезете.
>1. Почему правильный ответ - икс под номером 2? Ведь -2pi/3 лежит в III четверти, где sin < 0, а 2pi/3 - во II, где sin > 0.
У тебя каша.
Есть уравнение, видимо, решая его, мы где-то получили условие что синус должен быть отрицательным. Т.е. мы имеем, что либо икс равен первому выражению, либо второму, но синус от него точно отрицательный. В таком случае скобки расставлены правильно.
После этого мы должны найти все точки, которые нам подходят, потому что это все еще система. Значит отбрасываем первую серию корней. На втором пике абсолютно верное решение.
Алсо, решение написано безграмотно. Нужно от системы переходить к другой системе и никак иначе.
Бесконечно малая это не число...
>У тебя каша
Можно конкретнее, почему каша?
>мы должны найти все точки
Что тут ещё искать? У нас два икса, выбери, какой подходит, да и впиши в ответ.
>На втором пике абсолютно верное решение
Почему верное? Только что проверил оба варианта, подходит только мой.
>Нужно от системы переходить к другой системе
Можешь привести пример перехода? И когда можно переходить от системы к... эээ... обычному решению? Как это по-математически называется? Мне это очень важно.
> подходит только мой.
А второй какой? В ответе написан только один, в конце написано, поэтому нам подходит только одна точка. Ответ на вопрос почему каша смотри выше.
>Можешь привести пример перехода? И когда можно переходить от системы к... эээ... обычному решению? Как это по-математически называется? Мне это очень важно.
Переход называется равносильным, если решение двух систем совпадают. В решении же написан просто набор каких-то уравнений и неравенств, которые почему-то отбрасываются и видоизменяются. Оно абсолютно верное, но понять его можно, только если знать как решать подобное.
>первая серия даёт корни, лежащие на пересечение третьей и четвёртой
На твоём пике решавший перепутал числитель со знаменателем - рассуждает о 3π/2 когда у него 2π/3 которое строго во второй
А как её тогда понимать? Арифметические действия с ней можно проводить как с обычными числами.
>откуда ты узнал о бесконечно малой и математике вообще
Из книжки.
Вот определили там стандартную часть числа как вешественное число, нестандартную как бесконечно малую. Но ведь там подразумевалось что бесконечно малая это число в процессе этого определения. Как и корень из единицы, такого числа нету, которое в квадрате дает минус один, но абстракция допуска существования такого числа дала формулу эйлера, разрешение проблемы расхождения рядов типа 1/1+х^2, колебания и т.д.
> Арифметические действия с ней можно проводить как с обычными числами.
Что это значит?
>Из книжки.
Какой? Кто тебе ее посоветовал? Где взял?
Что операции сложения, умножения, возведения в степень, обратные к ним у них определены, и запрещено деление на ноль из за неопределенности результата.
Все эти операции я могу определить для букв, слонов и двача. И это не делает бесконечно малую буквой словом или двачем.
Не проецируй с математики на двачи с буквами. а+б=/=б+а.
Там определены операции по всем группам и категориям, с абелем и всем остальным. Даже можно сказать поле гиперреальных чисел.
И вообще, идея была представить бесконечно малую как непериодическую бесконечную дробь.
>А второй какой?
Ну вот же(пик 1), два корня, автор выбирает неправильный, после чего пишет какую-то херню. См.
Спасибо за объяснение.
У меня ещё несколько вопросов.
1. (Пик 2) Такое вообще законно? И то, что он вписывает в ответ простое число? А если я его вставить захочу в исходное уравнение, мне тоже представить, что это типа радианы? А если я захочу корень с pi вставить? Мне в обычном квадратном уравнении его как число что ли считать?
2. (Пик 3) Я не очень уверен в том, что понял, как они вычислили, что pi/3 не входит в данный промежуток. Единственная версия - они поделили 3,14 на 3 и посмотрели где лежит это число.
3. (Пик 3) Когда мы решали неравенство, что мы конкретно искали? Потому что я это понимаю, как "Схематично построить параболу и взять те промежутки, что по бокам от ветвей, т.к. ищем >= 0".
Я могу все определить так, что будет работать, было бы желание.
Почему тогда не определяешь?
Как обмазываться геометрическими доказательствами?
Почему в математике инфиксная запись выражений прижилась? Постфиксная для человека кажется намного естественней и во многих естественных языках встречается, в некоторых странных случаях префиксную можно. Но инфиксная...
2 2 + это же естественно. Или, в крайнем случае, + 2 2. А вот 2 + 2?
2 2 + это же естественно. Или, в крайнем случае, + 2 2. А вот 2 + 2?
Какая литература mustread для решения олимпиадных задач -диофантовых уравнений?
Нужно кушать испражнения других олимпиадников. Вкусишь их говнеца - познаешь их секреты.
а+б = аб, если а идет в алфавите перед б, во всех остальных случаях а + б = ба
У тебя член 4 см, ты его увеличил и стало 9, к своим 4 ты пристыковал имплант длиной 5.
8====+====3
Учебник открой, довен.
>2 2 + это же естественно.
В каком смысле естественно? Выглядит однохуйственно.
Антонасы, помогите разобраться. Имеет ли это смысл с математической точки зрения или совсем бред?
Теперь про бесконечно малые объясняй.
Если это не числа, то как их воспринимать? Как абстракцию очень маленького числа?
>Как абстракцию очень маленького числа?
Нет.
>Если это не числа, то как их воспринимать?
Как написано в определении, так и воспринимай.
Математика это не то, что везде можно пощупать потрогать и представить. Это наука про обобщение и закономерности.
Ну начнем с того, что при такой замене, катангенс не будет так выражаться. Подумай почему.
Подсказка, взятие корня - плохое действие.
Да и вообще, идея заменть в системе выражение, содержащее 2 переменные - путь в никуда.
Мы не можем однозначно выразить котангенс через синус? А если поставить +/- то было бы верно?
Из системы ниже можно выразить переменные, а затем подставить в уравнения.
Хотелось бы узнать насчет логики рассуждения. Она верна? Можно ли таким образом решить эту систему? Если нет, то как бы рекомендовал действовать?
>А если поставить +/-
Что это значит?
Если ты имеешь в виду решить две системы в оной с плюсом, а в другой с минусом, то да.
Я уже упоминал, что идея ввести третье неизвестное, зависимое от двух других - идея плохая. Я бы, сложил два уравнения.
>Если ты имеешь в виду решить две системы в оной с плюсом, а в другой с минусом, то да.
Именно.
>Я бы, сложил два уравнения.
Складывал и отнимал, но это не привело меня к успеху. Ладно, буду думать.
Но ведь ноль это единственное реальное число которое подходит под определение бесконечно малой -а<0<a.
И почему нельзя представить бесконечно малую как непериодическую бесконечную дробь?
Тебе нужно вообще смотреть в теорию чисел. Так изолированно диофантовы не решить.
В порядке возрастания сложности:
Ленинградские кружки
Школьные математические кружки: Четность
Школьные математические кружки: Делимость и простые числа
Школьные математические кружки: Теория чисел
Алфутова Теория Чисел / Прасолов Задачи по алгебре, арифметике и анализу - В первой мало решений, но их можно найти на problems.ru, во второй много дополнительных тем. Обе уже не простые.
Этого должно хватить, чтобы удовлетворить интерес, но если хочешь можешь еще навернуть Серпинского Теория чисел, "104 number theory problems" и "Elementary Number Theory" издательства Springer.
Определение приведи сюда
Я тебя в самом начале сказал ещё, что бесконечно малая это не число.
Если тебе нравится нестандартный анализ, где бесконечно малые это число, то нужно рассматривать не R, а другое множество - гипердействительные. Потому что аксиома Архимеда исключает бесконечно-малые числа.
Да, 0 бесконечно малое, но от него нету толку.
Бесконечно малым называется неотрицательное число t такое, что для любого положительного x верно t<x.
>ты: Как все таки пнимать бесконечно малую? Я могу её представить как дробь 0.00...бесконечное количество нулей...1?
>я: Бесконечно малая это не число...
>ты: А как её тогда понимать? Арифметические действия с ней можно проводить как с обычными числами.
Вот мой ответ ещё. Остальное не я писал.
Когда говорят о бесконечно-малых, имеют ввиду бесконечно-малые в классическом понимании. В классическом понимании бесконечно малая это последовательность стремящаяся к нулю.
Если попытаться определить бесконечно малую в R как
>Бесконечно малым называется неотрицательное число t такое, что для любого положительного x верно t<x.
то получается, что t<=t, причем равно только когда t=0. Такого быть не может.
Чтобы всё было пучком вводят такое определение: t - бесконечно малое, если t+t+t+...+t<1 для любого кол-ва t. Но тогда нарушается аксиома Архимеда, которой обладает R, она гласит, что если a<b, то a+a+a+...+a>b, при каком-то кол-во a. Поэтому вводят множество *R, где аксиома Архимеда не выполняется.
Представлять бесконечно-малые как 0,000...01 ты не можешь, т.к. это число действительное.
Добавлю, что в *R
>Бесконечно малым называется неотрицательное число t такое, что для любого положительного x верно t<x
это выполняется. Пусть r<1 действительное число и t - бесконечно малая. По аксиоме Архимеда в гипердействительных она работает, но не для всех чисел найдется такое n, что nr>=1, тога nt<1<=nr, поэтому t<r.
Докажи что f(a+b) = f(a)+f(b) и f(ab)=f(a)f(b)
А разве изоморфзим так доказывается?Равенство должно быть не между двумя РАЗНЫМИ операциями?
>Равенство должно быть не между двумя РАЗНЫМИ операциями?
Где это в твоём определении написано?
Тогда как к ней относится? Так же как к мнимой единице? Числа квадрат которого равен минус одному не существует, но мы допускаем что оно существует чтобы решать под сабатон по кругу?
Относится к бесконечно малой как к абстракция непрерывности числового ряда?
И почему бесконечная непериодическая дробь не подходит, состоящая из одних нулей и только где то там на бесконечности имеющая числа отличное от нуля? Она бесконечная, сколько её не умножай она останется меньше любого наперед заданного.
>Числа квадрат которого равен минус одному не существует, но мы допускаем что оно существует
Это неверный подход. Математика это про модели, хотим такую построим, хотим - другую.
>Относится к бесконечно малой как к абстракция непрерывности числового ряда?
Почему к абстракции? Это сходящийся ряд.
>И почему бесконечная непериодическая дробь не подходит, состоящая из одних нулей и только где то там на бесконечности имеющая числа отличное от нуля?
На секундочку. Как ты собираешься дать определение такой дроби? Обычная бесконечная дробь является точкой, являющейся объединением всех частичных множеств(если мы определим число как множество от нуля до этого числа, для наглядности). А как ты определишь свою дробь? Чтобы еще нагляднее показать тебе абсурдность твоего определения рассмотрим ситуацию.
Вселенная бесконечна, но на ее краю находится Васян. Ты говоришь, что начиная с этого момента у нас не будут встречаться никаие числа в записи кроме нуля, а потом говоришь, что после нулей идет 1.
А вообще, неплохо было бы освоиться в школьной программе.
Я про бесконечно малую нестандартного анализа.
Я в ней освоился.
Я тебе про суть смысла определения бесконечно малой, а ты мне про школу. Ты меня понимаешь или нет?
Определять бесконечно малую через обычные числа не стоит и выше это уже упоминалось. И если бы ты нормально плавал в обычных числах понял бы абсурдность своего определения.
Хорошо, это не число.
Тогда что?
Ну я честно не знаю что тебе сказать кроме
А ты в обычном то анализе хорошо разбираешься?
Ты про дзета эпсилон или про что?
И про это в том числе. а лучше спросить как ты шаришь в элементарной топологии?
Никак.
Так может стоит начать с основ?
Как это поможет мне познать суть бесконечно малой и бесконечности вообще?
Ну я вот школьную программу знаю и немного в основах разбираюсь. Мне не составило труда за 10 минут понять что и куда.
У тебя не получается это сделать уже пол треда.
читай, для кого я написал блядь
Есть 2 подхода: стандартный и нестандартный. Стандартный - бесконечно-малая это последовательность
Нестандартный - бесконечно-малая это число.
Ты ваще нихуя не понимаешь. Хули ты его путаешь, блядь? Он тебе про нестандартный анализ, а ты про классику. В нестандартном анализе вводится расширение R - *R, где бесконечно-малые числа есть, т.к. там не требуется аксиома архимеда. Я выше написал уже кратенько, блеадь, на этом нужно было закончить.
Ты удивишься, но я это понял. Проблема в том, что он не расширяет R, а определяет все на обычных действительных числах.
Мм ок, извини тогда, пожалуйста. Невнимательно читал.
ОП-пик для следующего треда
по моему скучная пикча! постите смешное!
Сап, нужна хорошая книга по мануалу логарифма и тригонометрии, от А до Я. Желательно с практикой.
После тыщи же новый.
Любой школьный учебник? Матхпрофи?
>Нестандартный - бесконечно-малая это число
Какое число? Бесконечно малое. Но какова его суть. Тобишь что означает в расширенной системе?
Тригонометрия Гельфанд - совсем просто, для первого знакомства
Сканави - наработка техники. И логарифмы, и тригонометрия
Обратные тригонометрические функции С.И.Новоселов - После предыдущих
Если захочешь со звездочкой, то
Тригонометрия на вступительных экзаменах по математике в МГУ Фалин Г.И
Математика - абитуриенту Ткачук
Дальше - олимпиадные задачники. Их отдельно гугли
Зачем ты ему говна навалил?
:)))
Ничего не означает, блядь, ну не можешь ты его как число записать, как и не можешь sqrt(-1) записать. Числом оно называется потому что так принято называть элементы множеств расширения N и т.д.
Анончики, подскажите, пожалуйста.
В этом году дропнулся из универа, ибо МАТАНъ. Осознал, что проге там не научат никакой, а МАТАНъ мне не особо поможет тестовые задания на сервлеты и фреймы решать, чтобы работку получить.
Однако маман настояла на том, чтобы я получил ВО(корку). В общем, с ноября я на заочке, более-менее погромистском факультете, но МАТАНъ все равно есть, как ни крути.
Вопрос: что сейчас начать читать, чтобы не кикнули оттуда и не охуеть в первую сессию?
МАТАНъ у меня класса до 9-ого, потом забил, ибо работать начал.
С меня IT вакансия в гугле
В этом году дропнулся из универа, ибо МАТАНъ. Осознал, что проге там не научат никакой, а МАТАНъ мне не особо поможет тестовые задания на сервлеты и фреймы решать, чтобы работку получить.
Однако маман настояла на том, чтобы я получил ВО(корку). В общем, с ноября я на заочке, более-менее погромистском факультете, но МАТАНъ все равно есть, как ни крути.
Вопрос: что сейчас начать читать, чтобы не кикнули оттуда и не охуеть в первую сессию?
МАТАНъ у меня класса до 9-ого, потом забил, ибо работать начал.
С меня IT вакансия в гугле
Вот кстати, всегда было интересно про Сканави. Его что, действительно берут и подряд все решают? Это же ебануться можно.
2-ух томник Фихтенгольца или Шварцбурд алгебра и анализ для ПТУ.
Зорич, Математический анализ
Точно так же, как и с любым задачником по любому предмету. Сколько тебе самому нужно, столько и решаешь.
Аноны, а в чём профит разложения в ряд Лорана в разных точках?
Можно же, например в полюсе разложить? А в существенно особой точке?
В чем преимущество по сравнению с рядом Тейлора? Я так понимаю, что чисто быстрее сходится и качественно показывает особые точки.
А где это требуется кроме задач на втором курсе я вот чёт не могу привести пример такой задачи... (Из физики, например, или экономики)
Господа, помогите решить задачу.
Есть большая таблица записей 5000 строк и 200 столбцов.
Есть массив условий 5 столбцов и 600 строк.
Нужно за меньшее время найти все записи по этим условиям.
Реализовал алгоритм на vba, но он пиздец как долго ищет и зависает, примерно 1,5 часа. Как всё это дело ускорить?
Есть большая таблица записей 5000 строк и 200 столбцов.
Есть массив условий 5 столбцов и 600 строк.
Нужно за меньшее время найти все записи по этим условиям.
Реализовал алгоритм на vba, но он пиздец как долго ищет и зависает, примерно 1,5 часа. Как всё это дело ускорить?
>А где это требуется кроме задач на втором курсе я вот чёт не могу привести пример такой задачи... (Из физики, например, или экономики)
на хуй пошёл отсюда.
Уже все задачи на множества прорешал?
Я не буду тебя посылать в ответ. Ты сам когда-нибудь поймёшь, что был неправ.
Тобишь ты будешь отрицать что величайшие математики во всей истории были физиками, химиками, астрономами, юристами, бухгалтерами, кем угодно но только не математиками?
>величайшие математики
>Галуа, Дедекинд, Гильберт, Нётер, Андре Вейль, Лере, Колмогоров, Гротендик...
это только малая часть.
Как ты удачно проигнорировал гаусса, ферма, римана, ейлера, ньютона и многих других.
Есть такая задачка:
Высота цилиндра равна диаметру шара, а объёмы этих тел равны. Найдите отношение площади полной поверхности цилиндра к площади поверхности шара.
Площадь поверхности шара это 4ПиR^2. Площадь полной поверхности цилиндра - это 2ПиR(H +R)
Я нашёл H цилиндра через равенство объёмов, подставил, а дальше ответ получается 1,5. В ответах к этой задачке есть только варианты с квадратными корнями. На пикче ответы к этой задаче. Пожалуйста подскажите на каком месте моё решение зашло не туда.
>H цилиндра через равенство объёмов
Точнее взял из условия. Где H = 2R
Где R - это радиус шара, а не цилиндра
Ответ (1+корень из 6)/3
А не получалось у меня,потому что я забыл, что радиус цилиндра НЕ равен радиусу шара.
Как доказать, что метрическое пространство сепарабельно?
ибашиш такой па тапалагическому прастранству...
Задал вопрос, а получил в ответ ещё один термин. Что такое топологическое пространство?
>нихуя не понимающий заочник
>Зорич
Толсто
Какое? Докажи, что в нём есть бесконечно плотное счётное множество. Например в R это Q.
мочух нахуй ты забанил блядь
Сепарабельно тогда и только тогда, когда у него есть счетная база.
Множество А всюду плотно в X, если [A]=X
И как это проверить?
Например на множествах рациональных и вещественных чисел
я вообще другой анон, просто интересно
Насколько понял: в R можно рассмотреть множество, состоящее из точек, координаты которой рациональные числа. А Q - счётное множество.
Что такое база?
Короче, ты выбрал литературу не для своего уровня сложности
То что хотел уже доказал. Сепарабельность доказывается по другому. Ты просто привёл ещё один термин.
Вводишь действительные числа, доказываешь, что между любыми дейст. числами есть рациональное. От сюда получается, что любая окрестность действ. числа пересекается с Q и т.к. Q счетно, то R сепарабельно.
Как найти сумму произведения известных рядов? Лямбда в степени n: 1/(1-lambda)
Всё остальное гиперболический синус. А вот что делать с их произведением непонятно
Всё остальное гиперболический синус. А вот что делать с их произведением непонятно
Говно вы, а не математики. Только строите из себя
http://faculty.etsu.edu/knisleyj/calculus/final.pdf
Бесплатно и без смс современный начальный курс. Требуется только знание английского и логическое мышление. Может быть, что нибудь из школьной алгебры, сам найдешь и повторишь. Ты же айтишник, должен знать английский и уметь в гугл.
На русском кроме Зорича ничего нет, но его лучше отложить до поры.
Фихтенгольцы и прочие годятся разве что для туалетов. Понятия не имею, как там на заочке, но на очке не мешало бы разбираться в лекциях и рекомендациях того маразматика, что читает тебе курс, потому что драть на экзамене будет как раз по своему курсу. Мысль понял, надеюсь.
>На русском кроме Зорича ничего нет, но его лучше отложить до поры.
Нет. Зорич отвратный учебник для пидорасов. Лоран Шварц хороший, или Рудин, но стиль Рудина мне не нравится. Фихтенгольц хорош, т.к. быстро и просто поясняет основные темы.
Не пойму откуда получается 1/sqrt(lambda)
Преобразовал к виду как на втором пике, в итоге получаем пик 3, который в пределе будет пиком 4, но вот откуда получается корень из лямбда в знаменателе?
>поясняет
Ясно.
пояснился от тебя по всем кольцам над модулями
пояснил тебе полиномом Лежандра, проверяй
Смысл читать Зорича? Если ничего кроме программы вуза не нужно, то по Фихтенгольцу за вечерок можно всю программу освоить. Если нужен тру анализ с тапалогиями-гамалагиями, то лучше читать Рудина, Львовского или Шварца, а не ебучего Зорича, где открытые множества появляются во 2-ом томе.
Ахуеть вы снобы. Съебите нахуй отсюда в паблики своих мехматов.
За вечерок? Это как? Я буду читать его минимум полгода и всё-равно не пойму минимум 30% книги.
>МАТЕМАТИКА ДЛЯ НАЧИНАЮЩИХ 32
>Говно вы, а не математики
Ну, технически все верно...
Я видать совсем, аноны. Не могу доказать, что если в множестве А есть а элементов, а в Б - б, то в А^Б их - а^б. Почему их не аХб? Поясните аутисту.
А^B - это по определению множество всех функций из B в A. Пусть в B ровно b элементов. Будем считать, что они занумерованы числами 1, 2, ... , b.
Элементы множества A будем называть буквами.
Каждую функцию из B в A можно тогда представить строкой из b букв.
Первая буква - это образ 1-го элемента B, вторая буква - образ 2-го элемента B, ... , b-я буква - образ последнего элемента B.
Например, пусть B = {1,2,3}, A = {p,q,r,s,t}.
Строки pqr и rrt описывают две разные функции.
Пусть во множестве A ровно a разных элементов.
Тогда первую букву в строке можно выбрать a способами, вторую букву - тоже a способами, ... , последнюю букву - опять a способами. Итого возможно a×a×...×a = a^b различных строк.
ЧТД.
С помощью арифметики ординалов доказательство прямо обобщается на случай, когда A и B бесконечны.
А^Б - множество всех функций из Б в А, т.ч. для каждого элемента Б возможно соответствие любому элементу А. Считай: для первого элемента Б существует |А| соответствий, для второго тоже |А| и т.д. получаешь |Б| множителей каждый из которых - |A|, т.е. всего |A|^|Б|
>по Фихтенгольцу за вечерок можно всю программу освоить
Разуплотнился от тебя на всё бесконечномерные пространства.
И с такими людьми я на одной борде сижу...
Грубо, есть два стула. На одном число точенные на другом буквы дроченные.
Каждому числу с одного стула ты можешь поставить в соответствие любую букву с другого стула. И так с каждым числом. Вот и получается что количество вариантов а^б
Бамп, помохите. Почему у меня теряется делитель?
Такие же мысли у меня, когда кто-то советует Зорича. Где, повторюсь, открытые множества появляются во 2-ом томе, когда во всех нормальных учебниках о них говорится сразу после ликбеза по множествам.
Где ты там корень из лямбда в знаменателе в результате увидел?
Че ты хочешь вообще непонятно.
Умножил на лямбду весь пример значит изменил его на константу.
Тогда уж лучше сразу бурбаков с тапалагическими инъекциями советуй.
Пиздец, фихтенгойц поясняет охуенно у него. Нет, люди добрые, ну вы только посмотрите на толстого дауна. Он математику по фихтенгойцу учить собирается...
Правильный ответ по учебнику - первый пик с лямбда в знаменателе. А у меня не получается
Сейчас читаю Рудина. Что с ним не так?
Исходное уравнение какое?
Это поиск резольвенты ИУ Вольтерра с ядром K(x, t)=x-t
А почему нельзя размышлять так? Есть а элементов множества А. Каждый из них можно записать в строку со всеми показателями степени из множества Б (которых б штук). Получается а строк по б элементов в каждой, и этим исчерпываются все возможные комбинации записей вида а^б. ЧЯДНТ?
А есть непозиционные и в тоже время пригодные системы ?
Система счисления Русов
А математику придумали жиды ?
Если ты о той, с которой знакомы большинство, то да.
Ну все перехожу на целковой,полушку,четвертушку и осьмушку
>Каждый из них можно записать в строку со всеми показателями степени из множества Б
Сам так решил или кто то сказал?
Бля, пацаны че-то я поехал, функция на пикриле строго возрастающая или нет?
Нет. Строго возрастающая означает неубывающая. А у тебя она убывает на промежутке
Анон, помоги по терверу.
Среднее кол-во золота, дропающееся из 5 сундуков равно 125.
Значит ли это, что шанс получить 50 золота из 5 сундуков равно 40%
125 золота = 100%
50 золота = x
x = 50 * 100 / 125 = 40
Ход мыслей верный?
Среднее кол-во золота, дропающееся из 5 сундуков равно 125.
Значит ли это, что шанс получить 50 золота из 5 сундуков равно 40%
125 золота = 100%
50 золота = x
x = 50 * 100 / 125 = 40
Ход мыслей верный?
каком промежутке
Строго возрастающая на левых и правых полуосях. На всей прямой, конечно, нет. Просто по определению строгого возрастания
Сам, очевидно. Просто для оценки числа возможных комбинаций.
Ты далбаебина тупая, я его челику посоветовал чтобы он из вуза не вылетел, ему больше и не надо. А ты тут сразу крылья распустил и нахохлился, как "Фихтенгольц" увидел. И это не плохой учебник, просто читать его нужно в школе ещё.
Мне не нравится как он пишет.
я сам чайник, но вроде бы так: если неизвестно распределение, воспользуйся нормальным. и оцени скок тебе нужно. через лапласа как-то неравенство делается. или через предельные теоремы, там ты тоже как бы оцениваешь
мимо студент, не ссыте на меня за это, сам недавно закончил этот теорвер.(если шо у теюя 125 - мат ожидание, не забывай, есть куча теорем, которые напрямую с ним работают, в смысле что могут упростить тебе вычисление)
>фихтенгольца в школе
мимо судент который ничего кроме письменного не прочёл
Стандартный анализ нужно прочесть, и чем более просто он написан, тем лучше. Уловить суть предела, производной, интеграла, формулы-НЛ и рядов сможет и 5классник. Просто он написан в Фихтенгольце, в Шварцбурге "Анализ для ПТУ", ещё в Зельдовече вроде, но я не читал.
Прочесть нужно и математикам, чтобы в продвинутых курсах не возвращаться к тому, например, почему производная определяется именно так как она определяется.
А никто не думал сделать сервис типа linglualeo и подобного по изучению языков, но для математики? Или есть уже? А если нет, то предположительно почему? Ну, euclidea нашел только вроде.
Khan academy есть.
Ну, это же просто видеоуроки, оно не интерактивно как-бы. Нет, как это называют "геймификации".
Ты их на ютабе смотрел что ли? Всё там есть.
Курсера.
Матеманимус, рссуди меня со мной же.
Что в западных источниках понимается под high school algebra? Каки различия у нас и у них? Изучают ли у них начала анализа? И что ткое прекалькулус? Я думал это и есть начала анализа но там вроде не оно
Зашел бы на сайт, да глянул. Но, скажу, что конечно обычный учебник наш по арифметике как-то полнее освещает тему.
Что в западных источниках понимается под high school algebra? Каки различия у нас и у них? Изучают ли у них начала анализа? И что ткое прекалькулус? Я думал это и есть начала анализа но там вроде не оно
Зашел бы на сайт, да глянул. Но, скажу, что конечно обычный учебник наш по арифметике как-то полнее освещает тему.
Скачай учебник, да посмотри. Думаю даже на вики можно найти список тем.
>скачай
В пдф файлах живут вирусы
>Изучают ли у них начала анализа?
Зависит от уровня школяра
https://en.wikipedia.org/wiki/AP_Calculus например сдают, если собираются учить в колледже что-то хотя бы опосредованно связанное с математикой
Про программу алгебры и остальных курсов доступные школьникам можешь прочитать здесь например: http://www.malibuhigh.org/academics_hs_math
Вроде в большинстве штатов для выпуска нужно сдать четыре предмета из списка
Тогда он ми вирусы удалит
Хорошо, спасибо. Я вижу, книги по рекалькулусу бдет достаточно
>Просто он написан в Фихтенгольце
Охуеть история
Зоричодебил, проследуй нахуй, чёрт ебучий.
Последовал тебе на бесконечномерное пространство, проверяй.
Проверил, пространство сепарабельно.
>5классник
>Анализ для ПТУ
ну всё, чувствую себя отсталым. максимум, что смог выучить - доказательство теоремы стокса. пойду плакать
Когда читал книгу по дифурам, наткнулся на такое рассуждение.
Несложно видеть, что x = f(t), где t определено для всех значений t, является решением уравнения. Покажем, что эта формула охватывает все возможные решения. Пусть phi(t) - решение уравнения. Можно считать, что phi определена для всех t.
Откуда могло взяться последнее утверждение?
Несложно видеть, что x = f(t), где t определено для всех значений t, является решением уравнения. Покажем, что эта формула охватывает все возможные решения. Пусть phi(t) - решение уравнения. Можно считать, что phi определена для всех t.
Откуда могло взяться последнее утверждение?
Я думаю это обусловлено видом уравнения. Там уравнение линейное:
z' = lambda z.
Надо заботать матстат на уровень бога. Пока осилили двухтомник Феллера. Нужен задачник и что-то продвинутое. Присматриваюсь к учебникам МФТИ. Что посоветуете?
биолог-кун
биолог-кун
Статистика не относится к чистой математике, это отдельная наука. Тут в основном чистую математику изучают. Спрашивай у других биологов.
Ага, я и смотрю по комментам выше, как вы тут разбираетесь в "чистой математике". Пошел нахуй, комнатный математический говноед.
Тред для начинающих всё же. Сам иди.
Но ведь он прав, что ты распетушился тут. Статистика является прикладной областью, использующей аппарат теории вероятностей, всякую там комбинаторику, чтобы собирать, обрабатывать большие данные о каких-то явлениях и доказывать гипотезы, связанные с этими явлениями. Математика изначально не про это. И специально тебе о книгах по мат.стату здесь никто не пояснит. Иди в гугол.
Иди нахуй, шваль. Самая бесполезная борда из всех, ни одного специалиста.
Задавайте вопросы по специальности - будут нормальные ответы.
Математическая статистика - подраздел математики.
Да я тебя, шваль, спрошу про топологию, ты же нихуя не ответишь, комнатное хуйло. Матешу учить - это тебе не блоги вербицкого надрачивать. Выродень ебаная.
Про общую и что-нибудь не слишком сложное - вполне отвечу. Спрашивай.
Нахуй ты живешь, шизик? Ты же никогда ни одной теоремы не докажешь.
Моя личность к топологии не относится. Обещание спросить что-нибудь ты не сдержишь, как я понял?
Не знаю насчет матстата, но раз ты заговорил про высокий уровень и Феллера, то можешь позырить задачник Ширяева. Он по терверу
>Тут в основном чистую математику изучают
Биекцировался в рогатую псевдосферу клейна от этого
Закупорил тебя.
людииии. мне нужна помащь. Мне нужно найти такую f(x), что k*f(x)=f(x)
f(x) не равна единице
f(x) не равна единице
f(x) = 0
и не равный нулю.
прост забил написать.
И не равна нулю
f(x) = 3 из R -> Z/5
k = 6, например.
Советую тебе взять мой хуй в рот, пыль ебаная. Ты хоть ординалы складывать умеешь, макака? Небось даже бином разложить не в состоянии. Какая тебе комбинаторика? Лучше говна поешь, жопа.
Если kf(x) = f(x) для k != 1, то f(x) = 0.
Пруф.
km = m
=> km-m = 0
=> m(k-1) = 0
=> m=0 или k-1=0 // в R нет делителей нуля
k-1 != 0
=> m=0
>ординалы складывать
Двачной бетежке больше нечем гордится в жизни, кроме как складыванию чисел придуманных до него?
Я их и придумал. В прошлой жизни.
Алё, вот решение.
Что ты за хуйню доказываешь?
тому долбоебу просто линейная функция нужна была, а он неправильно домашку со слову учителя записал
Какая домашка в конце июля?
Ты как с людьми разговариваешь, говно.
Пошел интегралы решать, быстро
Сделайте мне из этого четырёхцветную карту, пожалуйста.
можешь какой-нибудь из секторов перекрасить в четвертый цвет
Да уж, что-то я ступил.
Дают ли книги типа Serg Lang - Basic mathematics и John Stillwell - Numbers and Geometry и им подобные, то что они обещают? Что скажете о таком вообще?
А что они обещают?
А где на arxive публикации искать по мат.исследованию рынков?
Как аксиому выбора доказывать?
Из чего будем выводить?
По индукции
Привет, анон. Решаю задачу по матстату, попалось нетипичное условие.
Случайная величина фи задана законом распределения Fфи(х)
A(arctg(x) + пи)
x принимает значения от минус до плюс бесконечности. Найти коэффициент А и всю хуйню.
В примерах до этого F было разбито на три интервала:
0 если х < m
(0, 1) если х в интервале [m, n]
1 если х > n
И все действия происходили со вторым интервалом с областью значений (0, 1). Сейчас область значений выглядит странно.
Вопросы:
1. Правильно ли я понимаю, что речь идёт о радианах и область значений будет конечна и связана с областью арктангенса -пи/2 - пи/2 (ебал я вероятность -200 при больших отрицательных х).
2. Насколько я понял, для нахождения А нужно найти ф-цию плотности и пользуясь тем, что её интеграл равен 1, как-то найти А. Ф-ция плотности есть: 2А/(х2 + 1). Как найти А? Интегралы немного решал, но как найти А из готового решения пока не понимаю. Подскажите, пожалуйста, куда копать, я что-то не уверен, что уловил логику.
Случайная величина фи задана законом распределения Fфи(х)
A(arctg(x) + пи)
x принимает значения от минус до плюс бесконечности. Найти коэффициент А и всю хуйню.
В примерах до этого F было разбито на три интервала:
0 если х < m
(0, 1) если х в интервале [m, n]
1 если х > n
И все действия происходили со вторым интервалом с областью значений (0, 1). Сейчас область значений выглядит странно.
Вопросы:
1. Правильно ли я понимаю, что речь идёт о радианах и область значений будет конечна и связана с областью арктангенса -пи/2 - пи/2 (ебал я вероятность -200 при больших отрицательных х).
2. Насколько я понял, для нахождения А нужно найти ф-цию плотности и пользуясь тем, что её интеграл равен 1, как-то найти А. Ф-ция плотности есть: 2А/(х2 + 1). Как найти А? Интегралы немного решал, но как найти А из готового решения пока не понимаю. Подскажите, пожалуйста, куда копать, я что-то не уверен, что уловил логику.
Мол научат математически думать, а не просто помнить все формулы.
Есть одна рулетка. В ней играют числа от нуля до 99999.
Суть игры в том чтобы поставить ставку на одно из двух, какое сейчас выпадет число, больше 5250 или меньше 4750.
Если число попадает в промежуток между 4750 и 5250 все деньги идут к казино.
Шанс выигрыша 47.50%
Какая выигрышная стратегия/какую книжку читать чтобы самум вывести стратегию?
ее нет. Чтобы это понять, пройди какой-нибудь супер простой курс по терверу или статистика на курсере/степике/ютубе
Малореалистично, но сам не читал.
А, читал как-то книгу Барбары Оакли A Mind For Numbers и сопряженный курс Learning how to learn на курсере.
Смесь научпопа, советов по организации учебы и мотивационных кулстори. Ну такое.
Один толковый совет оттуда помог мне в моем аутизме - начал учить хуйню по таймеру, делая перерывы. Кроме того, повторял материал через определенные промежутки, последовательно. Вроде стал лучше запоминать, особенно говно всякое. Но это субъективно. Лучше не терять времени и учиться самому. В том числе, учиться запоминать, обучаться и так далее.
>А, читал как-то книгу Бурбаки Оакли
Пора завязывать с бурбаками
Можно подробнее?
>математически думать
Что ты под этим подразумеваешь?
Вот вы тут типа математики, а за множества мне пояснить так и не смогли.
>множества
Что за них пояснять? Не существует их.
Так куча математиков рассказывают о всякой там геометрической интуиции и прочее.
ПОясните мне за бином ньютона простыми словами. Я про разложение для не целых чисел.
>Не существует
Филсбэдмэн
Читаю матлогику Колмогорова. Это какой-то пиздец. Первые главы написаны на уровне коррекционной школы для дельфинов-даунов, а как началась булева логика, то я каждое второе утверждение не то что доказать, даже просто понять не могу.
Скорее, у тебя просто нехватка оперативки. Сконцентрируйся, не читай по нескольку словосочетаний за один раз. Это просто дело привычки.
Бля, такая жиза. Всю жизнь с этим проблема. Из-за этого не могу лекции слушать в универе.
другой анон
>Булева логика
Но это же совсем для детей.
У Колмогорова особая, уличная булева логика. Это надо видеть.
В чём её особенность?
>ZFC
Но она ведь противоречива.
Нет, её непротиворечивость следует из утверждения о существовании одного какого-нибудь большого кардинала. А существование таких кардиналов, в общем, очевидно как дважды два четыре.
>её непротиворечивость следует
Только относительно какой-нибудь другой противоречивой системы.
>А существование таких кардиналов, в общем, очевидно как дважды два четыре.
Не думаю.
Аргументы?
Первое - Теоремы Гёделя о неполноте
Второе - Аргумент такого же уровня как "ну это очевидно".
Пожалуйста, сформулируй названную тобой теорему о неполноте.
Ты прекрасно понимаешь о чём я. Из неё следует, что выражения как "её непротиворечивость" могут быть только относительно какой-то другой системы.
Доказывать непротиворечивость можно не только средствами формальных теорий.
Почему я должен доверять неформальным аргументам?
Ну, это уже сорт оф парадокс Кэрролла у тебя.
Бамп
Не понимаю, чего ты хочешь. Для целого случая формулу ты знаешь, при нецелой степени такой же формулы нет, но можно приблизить выражение сколь угодно близко рядом Тейлора. Раскладываешь по Тейлору = получаешь, что хочешь.
Ньютон с эйлером выводили всю теорию бесконечных рядов из формулы бинома ньютона. Я хочу понять как.
нифига себе ты годно запрос сформулировал. Почти так и поняли тебя.
Ньютон -- это историческая математика, которая сейчас построена очень по-другому, поэтому сомневаюсь, что тут кто-то тебе ответит
Суть то была в том чтобы я поня как изначально ньютон показал как возводить многочлен в дробную степень, а потом натянуть на это знание теорию рядов.
Ну не знаю. Когда мне говорят, что ДАНО: ас=а, бс=с, поэтому (а+б)с=а+б, я тупо смотрю на это и не понимаю как такая хуйня вообще может быть ДАНА. К такому меня не готовили.
Каким образом ты собрался её "доказывать"?
У тебя анальная фиксация на обычных операциях сложения.
Раздрачивай поля с кольцами и понимай что "2+1" может иногда быть равно "облако"
Кстати, какая самая малоизученная область у математики? Я имею ввиду не такую которая появилась после вчерашней пьянки романа с перельманом.
Откуда вы только лезите с такими вопросами, долоебы?
Ну вот к примеру могу сказать, что, очевдно, самая неизученная область это еще не открытая.
>ас=а, бс=с, поэтому (а+б)с=а+б
(a+b)c=c же, не?
Как проверить, что 2017 - это сумма квадратов?
(a-ib)(a+ib) = a^2 + b^2 = 2017
a=?
b=?
2017 простое число
>(a-ib)(a+ib) = a^2 + b^2 = 2017
a, b в таком случаи определенны не однозначно.
Я вот недавно придумал новую область математики. Пока вроде мало кем изучается.
>2017 простое число
бля, это лишнее. жара.
Оно вроде её последнее простое число.
я вот по остатком от деления на 4 смотрю, что-то не выходит.
Верно следующее, с точности до замены a на b.
a^2=2u+1
b^2=2v
=> b=2w
(2u+1)+4w^2=2017
u+2v=1008
Непоняно, короче
Сап. На связи школьник, 16 лвл(9 класс). Проблема такая, весь 8 класс сильно дрочил математику с репетитором, но учитель конкретно дизморалит, хуево объясняет тему(серьезно), график учебы такой: объяснение — практика в оставшееся от урока время, на след. урок самостоятельная. Из-за этого вышла 3 по алгебре и геометрии, + уже в последнюю четверть нет желания посещать уроки.
Конкретно у меня завал по анализу графиков, точнее по выводу области значения и т.д., сами графики и их формулы я знаю, стоит фиксить или хуй с ним?, тему с "убыванием и возрастанием графика вроде понял.
Задачи которые через квадратные уравнения тоже очень сложно составлять(составляю планы, но часто они неправильные), знаю что фиксить надо, покидает мб советов.
Ну и по классике, устный счет хуже не куда, главная моя причина 3, ибо часто ошибаюсь очень глупо.
Собираюсь накатить пикрилы(задачник какой-то уберсложный, хз как его решать)
Конкретно у меня завал по анализу графиков, точнее по выводу области значения и т.д., сами графики и их формулы я знаю, стоит фиксить или хуй с ним?, тему с "убыванием и возрастанием графика вроде понял.
Задачи которые через квадратные уравнения тоже очень сложно составлять(составляю планы, но часто они неправильные), знаю что фиксить надо, покидает мб советов.
Ну и по классике, устный счет хуже не куда, главная моя причина 3, ибо часто ошибаюсь очень глупо.
Собираюсь накатить пикрилы(задачник какой-то уберсложный, хз как его решать)
Вопрос у тебя какой?
если ты полоумный даун, то совет анона тебе не поможет
для таких вопросов есть /un
Если ты не способен решать легчайшие примеры, то тебе стоит перейти в школу для у.о., ибо здесь уже ничего не поможет. Это не троллинг, а хороший совет.
Нахуя тратить деньги на репетитора, наверное, сам аллах не ведает
Можно ли отделять аргумент тригонометрической функции от неё самой, при вынесении общего множителя(тр. функции) за скобки? т.е. cos(3x) - cos(x) = 0 -> cos(3x - x) = 0
Нет, триг функции не обладают дистрибутивностью.
Попробуй почитать Киселева.
???
Этот пост - квинтэссенция этого раздела. Сначала читаем, Бурбаки, потом выносим cos за скобку.
Что мы должны читать, и как сделать Бурбаки?
мимо другой анон
Лишняя запятая.
Хватит пиздеть о том, как плох раздел. Понятно, что люди разные. Кто-то учится в ВШЭ, кто-то учится элементарной алгебре. Это нормально.
К вопросу :
решение существует по теореме Ферма, но как его сконструировать?
решение существует по теореме Ферма, но как его сконструировать?
Напомни мне сколько решали ящик?
Что за ящик?
У вас мемес головного мозга.
Хочу создать свою личную криптовалюту, повелся на хайп.
Но вместо того чтобы компуктеры считали какую то белиберду цифро-буквенную хочу сделать так чтобы считалась математическая белиберда.
Сейчас я только додумался заставить комплекторы перебирать все числа от двух до бесконечности на простоту и вести в блокчейн записи уровня "2 простое число, 6 делится на 1-2-3-6, 147 делится на 3-7-21-49, т.д." Нахуя? Потому что могут. Ну и плюс потом в будущем, ящитаю, возможно понадобится кому то знать является ли число 1749369875873489562938483726489517389910463036490265936748495727659474191037703763535 простым или нет. Числа мерсена вычислять нихуя не подходит, так как только НЕКОТОРЫЕ из чисел мерсена простые, возможно что даже конечное множество. А еще они пропускают некоторые простые числа при последовательном увеличении степени
Есть еще что то такое чем математика может занять вычислительные мощности?
Если кто не понял что я хочу, математические проблемы которые пока не имеют способов решения кроме как тупым перебором.
Чтобы суть задачи вроде простая как два пальца обоссать асфальтом, типа последовательности простых чисел 2-3-5-7-11-13-17-19-23-29-31, а найти например 867 простое число, кроме как тупо перебирать все числа с калькулятором, невозможно было.
теорема ферма же a2+b2=c2
2017!=квадратику
Как стать аутичным математиком и посвятить все полностью матану ?
>Раздрачивай поля с кольцами и понимай что "2+1" может иногда быть равно "облако"
А как же тезис, что в математике все должно быть либо очевидно, либо доказано? В Винберге такой хуйни не было.
У меня опечатка. На самом деле бс=б.
Делай уроки
Основания не доказываются а выводятся.
Ты проецируешь арифметическую суть операции сложения на логические цепочки.
От того что ты скажешь оп пидор десять раз, умножишь на десять тобишь, оп не станет десятикратным пидором.
Нармалёк, но образование получить все же советую. Даже если хранить ровно по одному биту на число (простое, или нет), то для хранения информации о всех числах до того, что ты назвал нужно примерно 2 х 10^71 террабайт. Посчитал на вольфраме.
Значит хранить только найденные простые числа. Каждое число будет соответствовать блокчейну.
И что то это слишком дохуя. Посчитаю завтра на свежую голову.
Так а что делать-то тогда? Просто поверить? Не, ну нельзя же так просто говорить, что сегодня у нас аб будет равняться а. Я так какую угодно хероту смогу сконструировать.
Двач помоги, со следующего курса у меня будет вышмат.Хочу хоть что нибудь поучить заранее.Посоветуйте книжку.
Алсо я тупой
Алсо я тупой
> нельзя же так
Значит НЕ ЛЕЗЬ БЛЯДЬ, ДЕБИЛ СУКА ЕБАНЫЙ!!!.
Еще раз повторяю. У тебя анальная фиксация на арифметическом значении символа +.
другая теорема ферма, про остатки суммы квадратов при делении на 4.
Какие проблемы? Это следует напрямую из определения "сложения" и "умножения".
Справочник по вышке
Матфпроphi))
Как лучше аксиому выбора доказывать?
По индукции
По индукции?
Как считаете, есть ли какой-то потолок в интеллектуальном плане или все можно развить трудом и усердием?
К примеру, я вот хоть убей не понимаю как доказывается та или иная вещь в математике. В том же функциональном анализе замкнутость множества. Преподаватель как-то старался объяснить на лекции, все, и я в том числе, кивнули утвердительно, мол "ага, всё понятно, очевидно, тривиально!". А домой пришел и осознал, что я то ничего и не понял.
Или доказать положительную определенность линейного оператора. Через цепочку неравенств нужно вывести какую-то константу, которая как раз и будет доказательством положительной определенности? У меня единственная реакция - ЛОЛШТО?
В целом, по примеру, так сказать, по аналогии я смогу доказать для какого-то конкретного оператора, наверное, а вот сам этот алгоритм никогда бы не придумал.
Вот вернулся к сабжу, а может это мой потолок? К слову, очень плохо считаю устно, в магазине туплю, а дома все на листочке расписываю (даже сумму/разность дробей а я на третьем курсе матфака, стыдно).
К примеру, я вот хоть убей не понимаю как доказывается та или иная вещь в математике. В том же функциональном анализе замкнутость множества. Преподаватель как-то старался объяснить на лекции, все, и я в том числе, кивнули утвердительно, мол "ага, всё понятно, очевидно, тривиально!". А домой пришел и осознал, что я то ничего и не понял.
Или доказать положительную определенность линейного оператора. Через цепочку неравенств нужно вывести какую-то константу, которая как раз и будет доказательством положительной определенности? У меня единственная реакция - ЛОЛШТО?
В целом, по примеру, так сказать, по аналогии я смогу доказать для какого-то конкретного оператора, наверное, а вот сам этот алгоритм никогда бы не придумал.
Вот вернулся к сабжу, а может это мой потолок? К слову, очень плохо считаю устно, в магазине туплю, а дома все на листочке расписываю (даже сумму/разность дробей а я на третьем курсе матфака, стыдно).
Тоже интересно. Есть ли тут состоявшиеся математики с условно низким IQ?
аб=а из определения сложения не следует.
Сап, математики.
Прошу помощи: в каком порядке изучать материал, чтобы выйти на дискретную математику?
Из знаний: полузабытые квадратные уравнения, немного логарифмы, все.В школе все делал по ГДЗ, успел съебать из школы до ввода ЕГЭ, дальше сдирал у одногруппников. Я не тупой, просто всегда считал предмет не нужным.
Выучить хочу для понимания алгоритмов, которыми я каким-то хером увлекся, но очень сильно тону на всякого рода графах, хуяфах и этих всех умных вещах.
Прошу помощи: в каком порядке изучать материал, чтобы выйти на дискретную математику?
Из знаний: полузабытые квадратные уравнения, немного логарифмы, все.В школе все делал по ГДЗ, успел съебать из школы до ввода ЕГЭ, дальше сдирал у одногруппников. Я не тупой, просто всегда считал предмет не нужным.
Выучить хочу для понимания алгоритмов, которыми я каким-то хером увлекся, но очень сильно тону на всякого рода графах, хуяфах и этих всех умных вещах.
Повтори школьную программу
Двачую, этого более чем достаточно.
Собственно, дискретку и читают во втором семестре (в первом, как правило, предваряющая ее теория множеств и комбинаторика)
Спасибо.
Где ты тут увидел >cos(3x) - cos(x) = 0 -> cos(3x - x) = 0?
Привет, двачеры. Три года как закончил школу. Недавно появилось дикое желание решать алгебру. Хз почему. Так вот посоветуйте какие нибудь учебники, чтобы заново погрузиться в этот мир и изучить все по новой. Желательно, чтобы все было с примерами и объяснениями.
Я забыл, как вычислять производные функции, заданной в виде f(x, y) = g(x, y). Мне нужно найти уравнение касательной к эллиптической кривой y^2 = x^3 + x + 4 в заданной точке. Как найти производную?
d(f-g)/dy / d(f-g)/dx = dy/dx
Как такой способ дифференцирования называется в калькулюсе? Дифференцирование неявно заданной функции?
Хм, непонятно. Производную нашел: она равна y' = (3x^2 + 1) / 2y. Но в знаменателе стоит y. Как в таком случае найти касательную к эллиптической кривой?
Бля, я там напиздел со знаками, это производная неявно заданной функции.
Посоветуйте учебник геометрии для личностей с пониженным интеллектом.
Школьной? Аналитической?
Школьной планиметрии хотя бы. Да и чуть дальше не помешает.
Эксмо. Математика, справочник для поступающих в вузы.
Скажите что осваивают люди, в каком возрасте и как дабы не писать подобной ерунды.
Представим вертикальные углы a и b. Требуется доказать, что они равны.
Проведем смежный с углом a угол c. Так как они смежны
a+c=180
с=180-a
И все еще надо доказать что a=b. Это можно доказать лишь зная что, b+c=180 и тогда весьма тривиально получается
180-b=180-a=c
(180-180)-b=(180-180)-a=c-180
|-b|=|-a|=|c-180|
Но откуда мы знаем что угол "b" смежный с углом "c", как угол "c" смежный с "a"? Это надо теорему о накрест лежащих углах при параллельных прямых?
Или тогда угол в общем-то главное чтобы c обозначал один и тот же самый угол. То есть, один. Но он может тогда быть и на другой стороне, потому что он один.
Ощущение, что говорю об очевидных вещах, но эмоционально я ощущаю какую-то огромный прогал в знаниях и ощущениях и зашел куда-то в дебри.
Представим вертикальные углы a и b. Требуется доказать, что они равны.
Проведем смежный с углом a угол c. Так как они смежны
a+c=180
с=180-a
И все еще надо доказать что a=b. Это можно доказать лишь зная что, b+c=180 и тогда весьма тривиально получается
180-b=180-a=c
(180-180)-b=(180-180)-a=c-180
|-b|=|-a|=|c-180|
Но откуда мы знаем что угол "b" смежный с углом "c", как угол "c" смежный с "a"? Это надо теорему о накрест лежащих углах при параллельных прямых?
Или тогда угол в общем-то главное чтобы c обозначал один и тот же самый угол. То есть, один. Но он может тогда быть и на другой стороне, потому что он один.
Ощущение, что говорю об очевидных вещах, но эмоционально я ощущаю какую-то огромный прогал в знаниях и ощущениях и зашел куда-то в дебри.
Это по определению. Берем смежный угол с А и называем его С.
А откуда мы знаем что он будет смежный с B тоже? Тоже по определению угла С?
>Проведем смежный с углом a угол c. Так как они смежны
Зачем что-то проводить, если смежные углы сами образуются?
Смежные углы — это пара углов с общей вершиной и одной общей стороной.
Это от подобного определения надо отталкиваться?
a и b и c, b - смежный с углом a угол, значит он с ним имеет общую вершину и общую сторону. А имеет ли он общую вершину и общую сторону с углом b? Ну, вертикальные углы... прямые так как углы вертикальные, то угол a имеет... ну прямые... эээ... и по этому угол c в общем-то имеет общую сторону с углом b, по скольку имеет с углом a, а угол a имеет с углом b не... чот как-то словоблудие какое-то у меня.
Там симметричная картинка. Нарисуй вертикальные углы А и B. Вне зависимости, какой C, какой D они будут смежные и с A, и с B.
Не могу найти в интернете издание именно от Эксмо.
Как запоминать теоремы? Надо зубрить аксиомы? Решать задачки со сходного? Еще что? Как запоминать дабы не выветрилось и потом обобщилось и все хорошее?
Поясните за математические структуры, чувствую в этом что-то очень глубинное. Что-то почитать небанальное на понимание.
Прими определённую формальную систему как истину и в ней доказывай теоремы и решай задачи.
В других формальных системах, обычно всё устроено очень сходным образом.
+1 вопросу, много раз видел упоминание "СТРУКТУРЫ" как некого математического объекта, но не сталкивался с содержательными вещами на эту тему.
Математической структурой называется следующий набор данных.
1. Множество G, называемое носителем структуры.
2. Возможно пустое семейство Ai множеств, называемых вспомогательными.
3. Семейство операций.
4. Семейство отношений.
Под операцией понимается отображение из прямого произведения нескольких копий G и, возможно, некоторых Ai во множество G.
Под отношением понимается подмножество прямого произведения нескольких копий G и, возможно, некоторых Ai.
Сап двач, есть одна задача: есть треугольник, в нем известны высота, угол из которой она выходит, сторона, на которую она падает. Так же при острой необходимости можно узнать сумму двух оставшихся сторон. Как найти оставшиеся стороны?
Находишь площадь как половину произведения основания на высоту и как половину произведения синуса угла на стороны, получаешь произведение сторон. Из теоремы косинусов выражаешь сумму квадратов сторон. Решаешь квадратное уравнение.
Поподробней?
Через полторы недели поеду на сухари под шконку на пятнадцать лет с УДО и с конфискацией имущества.
Какую литературу следует попросить у родственников чтобы выучить всю математику?
Киселев. Геометрия. Планиметрия и стереометрия.
для начала можешь почитать школьные учебники
повтори precalculus, например
Посоветуйте задачник по Алгебре.
->
math - Математика
Скорость борды: 4, количество тредов: 157, количество постов: 22577
Доска о модулях над кольцами, пучках на многообразиях и гомологиях с когомологиями.
=======================
пффффффф
Скорость борды: 4, количество тредов: 157, количество постов: 22577
Доска о модулях над кольцами, пучках на многообразиях и гомологиях с когомологиями.
=======================
пффффффф
Дяденьки, научите меня евклидовой геометрии.
Это много или мало?
А ты симпатичный?
Что имеют в виду, когда говорят "вероятность 7 к 12"
p=7/12 или p=7/(12+7) ?
За второй вариант поясни
Второй вариант трактовки - это 7 голосов "за" некоторую гипотезу A и 12 голосов "против" неё.
Немножко.
crickets практически. 4 поста в час. в /b тысячи их. но у всей сцы вместе взятой еще меньше.
Чисто из интереса, на математике ирл реально заработать? Типа теория вероятностей, комбинаторика, статистика, какие-нибудь ставки или игры, вот это всё? Просто я подумал, интересный вопрос
А все почему? А потому что рулеточек нету.
Нет, математика старше 8-9 класса - это чисто логическая игра, как шахматы. Ну, можешь на олимпиадках золотую медальку выиграть, но она скорее всего только позолочена снаружи.
Из 12 событий 7 впадет такими которые нам и нужны.
Твой топологический дефект хорош чтобы сосать несчетную сетку дзета нулей.
Ну ты и зануда. Я бы с тобой не дружил, если бы такое в жизни услышал
Значит пиздуй отсюдова считать несчетное множество
>несчетное множество
Не существует такого дерьма. Иди нахуй.
Хуя дебич к нам пришел.
Пересчитай мне все числа между нулем и единицей /Ь/ратиш
Между "нулём" и "единицей " из какого множества?
Кватернионов.
Всем здравствовать. Надеюсь, что у вас не очень хуесосят, ибо заебало.
Посижу пригляжусь, может вольюсь.
Вот мой скромный вклад в общак.
https://rutracker.org/forum/viewtopic.php?t=5020592
Чего, простите?
Чет тоже не понял. Кватернионы это ж группа из 8 эл-ов.
Как называется переход между решением задач к доказательству теорем?
Пидорство
Царский подгон
тогда комплексные числа - это группа из 4х элементов(сарказм)...
"осознание как использовать формальной системы"
Изучение математики.
Что значит improper integral?
Несoбственный интeграл.
Здравствуй, математический.
На пикрил, кажется, опечатка (9b^2). Или я сам где-то проебался?
С меня как обычно
На пикрил, кажется, опечатка (9b^2). Или я сам где-то проебался?
С меня как обычно
ты ошибся: в одном соучае основание - 3, в другом 9
стопэ, это я по ходу ошибся, а ты прав, времени нет сейчас
Изучение геометрии надо начать с зазубривания аксиом?
Я не знаю каким долбоёбом нужно быть, чтобы приходилось "зазубривать" аксиомы.
А с чего?
Киньте книг для закатывания в теорию графов. Чтобы там поясняли без расслоений топологических бесконечномерных колец над неабелевыми группами колец.
С решения простых задач, применяя всё больше и больше аксиом.
всё-таки ты ошибся а там всё ок
Это где такое?
Хех, помню тебя и твой тред в б
А я не помню.
Есть 2 стула... То есть дохуя узлов в сети, некоторые из них соединены между собой, т.е. стандартный граф. Каждый узел имеет координаты и отображается кругом с радиусом R (одинаков для всех узлов). Координаты выбраны таким образом, чтобы круги не пересекались и между ними было некоторое свободное место.
Вопрос: как нарисовать связи, используя квадратичные кривые Безье (см. пикрелейтед), чтобы кривая, соединяющая 2 узла, НЕ ЗАДЕВАЛА ДРУГИЕ УЗЛЫ? То есть как правильно выбрать то, что на пикрелейтед называется управляющей точкой?
Гугль/Яндекс находит только алгоритм построения самой кривой Безье, который мне не нужен - в SVG кривую строит сам браузер по 3-м точкам. А вот применительно к задаче отображения связей графа - ничего не смог найти.
Неделю уже сижу над этой задачей, начальник ругается, грит я тупая веб-макака, "пошел нахуй тогда отсюда, пошел, блядь, ничего не можешь сделать, пошел нахуй, говно". Помогите, братишки!
Вопрос: как нарисовать связи, используя квадратичные кривые Безье (см. пикрелейтед), чтобы кривая, соединяющая 2 узла, НЕ ЗАДЕВАЛА ДРУГИЕ УЗЛЫ? То есть как правильно выбрать то, что на пикрелейтед называется управляющей точкой?
Гугль/Яндекс находит только алгоритм построения самой кривой Безье, который мне не нужен - в SVG кривую строит сам браузер по 3-м точкам. А вот применительно к задаче отображения связей графа - ничего не смог найти.
Неделю уже сижу над этой задачей, начальник ругается, грит я тупая веб-макака, "пошел нахуй тогда отсюда, пошел, блядь, ничего не можешь сделать, пошел нахуй, говно". Помогите, братишки!
>грит я тупая веб-макака
Он прав. В /pr/.
Скажите. Предположим, что есть 1000 атомов, каждый из которых за минуту может расписаться с вероятностью 1/10. Как посчитать вероятность, что распадется 100 атомов? 50 атомов? 150 атомов?
Тьфу, не расписаться, а распасться, чертова автозамена.
https://ru.wikipedia.org/wiki/Схема_Бернулли
Пусть успех - распад атома.
p = 0.1.
Опыт - наблюдение за атомом по итогам 1 минуты.
Нужно найти вероятность ровно 100=m успехов в 1000=n опытов.
Она равна (nm)pm(1-p)n-m = 1000!/(100!900!) 0.11000.9900.
Что приблизительно равно 0.042 = 4.2%, согласно вольфраму.
Мне бы хоть одну решить. Вторая кажется какой-то легкой, но что-то в голову совсем ничего не лезет.
Спасибо. А еще, можешь помочь с пониманием функции биномиального распределения? Оно состоит из функции Бернулли и не понятной мне сигмы.
не, я спать
Ну, может как нибудь позже.
Или кто-нибудь другой.
Я пять раз прочитал первую задачу и я ее не понял. В каком вузе сидят долбоебы, которые придумывают такую поеботину?
Физмат лагерь, лол
Да ведь у нас и так почтинг маленький, а ты еще веб-няшек в /пр гонишь!
Если бы вшэ, я бы решил, ради смеха. А так - иди нахуй, школьник.
хз как это решается, напиши потом, анон, когда разберут
Рассмотрим замкнутую несамопересекающуюся кривую длины L. На ней отмечены N точек, с каждой точкой i связано вещественное положительное число xi. Сумма x1+x2+...xN больше или равна числу L.
Доказать, что существует круговая подстановка f чисел 1, 2, ... , N такая, что для любого j от 1 до N длина участка кривой от точки f1 до точки fj меньше или равна сумме чисел xf1 + xf2 + ... + xfj.
Уточнения.
Подстановкой называется биекция из множества {1, 2, ... N} в себя.
Она записывается в две строки, вверху прообразы, внизу образы.
Пример подстановки:
12345
52314
Мы записываем подстановки по нижней строке, например предыдущую подстановку мы бы записали как (5,2,3,1,4) или даже как 52314.
Под круговой подстановкой понимаются подстановки (1, 2, 3, ... , N), (2, 3, ... , N, 1), (3, ... , N, 1, 2), ... , (N, 1, 2, 3, ... ), а также (N, N-1, ... , 2, 1), (N-1, ... , 2, 1, N) и т.д.
Под fk понимается образ числа k.
Так, если f - перестановка 51234, то f3=2, f5=4.
Предполагается, что между точками с соседними номерами нет других отмеченных точек. Т.е. между точками 1 и 2 нет точек, между точками 2 и 3 нет точек и т.д.
По 2 а) могу сказать, что каждый следующий ход надо делать так, чтобы он перебивал по эффекту все предыдущие. Тогда в целом ты будешь ехать вниз либо по нечетным, либо по четным. По другим задачам ничего сказать не могу, голова раскалывается.
Если в b) опечатка, то каждый ход к увеличиваешь с единицы до бесконечности. Когда наткнешься на нужное число начнешь ехать вниз. Если опечатки нет, то никак. В с) жесть какая-то. Что за лагерь, концентрационный что ли?
Решение. Вырежем из листа бумаги несколько секторов диска. По условию секторов достаточно, чтобы выложить их них целый диск. Сектора расположены так, что касаются центром и перекрываются. Начнём двигать каждый очередной сектор. Будем двигать до тех пор, пока он не перестанет перекрывать предыдущий. Очевидно, рано или поздно получится целый диск.
Описывать это решение формально как-то влом.
Знаю математику на уровне конечного автомата, то есть в те же доказательства теорем не умею. Спасите меня. Как спастись?
Че то я в ахуе с ответов. Не беру в голову, нормальные задачи. Первая: http://www.problems.ru/view_problem_details_new.php?id=73617
Вторая:
Ты не знаешь на каком ты этаже - выше первого, или в подвале. Твоя задача просто проходить этажи, пока не попадется первый, но тебе надо идти в обе стороны, т.к. непонянто где первый.
Спускаешься на один вниз. Так k раз
Поднимаешься два раза на k
Спусшкаешься на один вниз. Так k раз
Теперь ты оказался там, где начал, но прошерстил k ближайших этажей. Видимо, первого не оказалось среди них. Повторяешься все, но берешь уже 2k. Потом 3k. Рано или поздно окажешься на первом и двери раскроются.
Про пункт с) не знаю, он какой-то хитрый, но готов поспорить на хабре уже где-то такую задачу разбирали.
Третью устно не скажу, но уверен, что здесь индукция по k. Порисуй на бумажке разные k, и посмотри сколько укладывается гробов в разные квадраты. Будет какая-то закономерность. Ее надо будет доказать по индукции
Подскажите как аксиому выбора доказывать?
По индукции, вроде
Подробнее можно? Где можно прочитать про это?
И где он тут аксиому выбора доказывает? Мы пытались с другом доказать и у нас намного больше пяти минут ушло, только так ничего и не получилось.
Мб в психушку пособие по шизе оформить норм идея как думаете? Чтобы всё свободное время математике посвятить. А то работать мамка гонит. А там всё время на работу будет уходить. Или норм? Кем кто работает, кстати?
Нормально. Я в психушке доказывал много важных теорем.
Расскажи, как там вообще? Пенсии хватает на жизнь?
Годно придумал
Ну ок, пойду тогда симптомы читать, по идее даже симулировать ничего не нужно, абулия, асоциальность и тд
Вполне. Я других психов обучал и заставлял свои доказательства проверять.
Лол, охуенно. Ну ок, решено тогда. В понедельник попрусь.
А где там доказательства?
Так во втором ведь не знаешь, какая кнопка что делает. А в первом не сказано, что можно воровать топливо у других машин
Вы тут типо математики, да? Да вы же питушары дырявые ,не более.
Про первую хуйню сказал, понял, что машины = бочки
Но вот со второй что-то не то.
По поводу 100 этажей очевидно, по поводу к - подозреваю, что на нужно тыкать на кнопочку сначала из предположения что к это 1, потом 2 и так далее.
>как аксиому выбора доказывать?
>аксиому
>доказывать
Я не шарю в этой теме.
А что такого?
Хочу сделать свою математику без блекджека и шлюх. С чего начать?
Видимо тут какая-то историческая ошибка, раз теорему называют аксиомой. Или ты еблан. Или ты троль.
В общем я требую пояснений.
Так пока что и не теорема, правильно всё называют. Я сейчас пытаюсь доказать её.
Аааааа, так ты просто еблан.
Давай по порядку.
В какой системе аксиом ее будешь доказывать?
Использовать в качестве управляющей точки ближайшую к двум нужным точкам третью точку.
zfc
Если имеется ввиду нарисовать кривую так чтобы она не заходила в третий круг, выбирать управляющую точку в таком месте, чтобы трегольник образованный этими тремя точками не содержал частей остальных кругов, ибо кривая безъе всегда заключена в многоугольнике построенном на выбранных точках.
ZF.
z.
.
Какой лучший учебник по алгебре из школьной программы ?
Как доказать, что F(A + B) = F(A)+F(B). F(X) - свободная группа, "+" копроизведение(в данном случае дизъюнктное объединение и свободное произведение соответственно).
Другими словами, мне нужно доказать, что свободные группы сохраняют копроизведение. Я могу доказать, что они изоморфны благодаря универсальному свойству, но насчёт равенства что-то идей нет никаких
Другими словами, мне нужно доказать, что свободные группы сохраняют копроизведение. Я могу доказать, что они изоморфны благодаря универсальному свойству, но насчёт равенства что-то идей нет никаких
Люто двачую, ибо мой друг из физмат школы по такому занимался. Это фундамент, но если захочешь чего-то олимпиадного, попробуй Шень Алгебра
Всем вечер добрый. Решал уравнение (пикрил 1). Вижу, что симметрическое уравнение, провёл замену t = x - 1/x. Получил дикие корни (а-ля пикрил 2). Wolfram показывает красивые корни (а-ля последний пикрил). Господа, где я проебался? С меня как обычно, наверное -- большое человеческое
Каким образом лучше доказывать аксиому выбора?
Быстрофикс
Тут теорема Ферма нужна вроде.
Может, Безу?
Нет, через безу сложно, аксиому выбора проще всего доказывать сведением к группе, а там уже через Ферма, как следствие.
Алсо в какой аксиоматике собираешься доказывать? А то мы щас насоветуем.
А правда, что с помощью ZFC можно воскрешать мёртвых?
Я тебе больше скажу, можно мертвым сделать кого-то при помощи ZFC.
Насколько я помню аксиомой выбора можно воскрешать мёртвых, так что ничего страшного.
Аксиоматика? о_0
В NBG буду пытаться.
Да они тебя приебашут так что сдохнешь
Каким образом "доказали" "теорему" Ферма если она ведёт к противоречию?
Это на самом деле тривиально.
До меня не доходит
Это прямое следствие теоремы Ферма.
Вот поэтому мы и гооврим про то, в какой аксиоматике работаем.
Анон, перепроверяй. Алсо как тебе тут поможет такая замена, если там только один коэф различный?
Если теорема Ферма имеет доказательство, то арифметика Пеано противоречива.
Это на самом деле довольно легко доказывается.
Да, ну чтож, это явно прорыв, быстрее пиши об этом во все издания, но не рассказывай нам, а то спиздим идею.
Куда написать можно?
Самое уважаемое заведение в нашей стране это т.н. Кащенка. За бугром тоже есть, но они не будут с рандомом непонятным разговаривать.
Индукция, не?
Ты где-то обсчитался. Так же разделил на х^2, сгруппировал, сделал твою замену, получил красивый ответ
>ведёт к противоречию
Какому?
Моё доказательство не конструктивно, так что не знаю.
Я, конечно, делаю только первые шаги в мат логике, но мне действительно стало интересно.
Как с ними связаться лучше?
А ты расскажи кому-нибудь ирл о своих достижениях, они тебя сами найдут.
Я боюсь рассказывать, вдруг спиздят идеи мои.
Тоже верно. Но ты к их специальному агенту подойди, тут можешь не беспокоиться, он не украдет. Либо сразу в патентное бюро беги, только без очереди, чтобы побыстрее, приходи и сразу кричи про то, что сделал. Тебя поймут, дальше пустят, а там уж и рассказывай свою тему.
В патентное бюро? Разве доказательства можно патентовать?
И можно подробнее про "специального агента"? И откуда ты так уверен в его честности?
Блять, объясните мне уже ряды и их сумм. А то я что русскую, что украинскую, что английскую с немецкой литературы читаю и все равно не понимаю.
Вот что я понял.
В книжках обычно пишут все в такой последовательности
Сперва поясняют что такое ряд. Ряд это функция аргумент которой проходит только целые значения, тобишь последовательность чисел получаемая с помощью определенного правила.
Потом объясняют что означает сходимость. Сходимость ряда стремление суммы ряда к какому то числу при стремлению количества суммируемых к бесконечности. Если при стремлении количества слагаемых к бесконечности сумма тоже стремится к бесконечности ряд расходится/сходится на бесконечность.
Дальше тестирование ряда на сходимость. Деление соседних членов ряда друг на друга, пределы, интегралы, даламберы, коши и прочая прочая которая проверяет действительно ли хвост ряда стремится к нулю.
Потом всякие радиусы сходимости с аналитикой и приведением к известным рядам.
Потом пишут простейший пример суммы ряда 1/1-х, объясняют почему он сходится только на промежутке (-1:1)
Потом я теряю нить разговора и возвращаю её когда мы уже находим суммы степенных рядов через экспоненты, арктангенсы с косинусами и и логарифмами.
Вот объясните мне как от прогрессий перешли к арктангенсам.
Все понимают математику, а я ублюдок и тупой мудак.
Запретите полоумным родителям рожать полоумных детей.
Запретите полоумным родителям рожать полоумных детей.
https://2ch.hk/math/res/3583.html
Когда-то был сделан тред по тому как научиться доказывать теоремы. У тебя тоже проблемы с этим?
И не только. Через некоторое время я забываю доказательства и не могу их восстановить из памяти.
Посмотри первую часть курса калькулюса от пенн юниверсити на курсере. Там это хорошо объясняется.
Имидж - самое главное в таких делах, и им светит срок, если они попытаются присвоить чужое. В патентном бюро можно патеновать открытия твоего уровня.
Двощь, для решения задачек по механики (и в дальнейшем для аналитической механики), какие разделы математики нужны изучить? Можно я остановлюсь на алгебре, анализе и дифференцировании? В чем различие их?
3 класс-кун
3 класс-кун
Нельзя. Щас уже лагранжианы для механики применяют.
>забываю доказательства
ДЕБИЛ ЕБУЧИЙ СУКА ТЫ!!!!!!
Сказано же, дебилу, запоминай саму суть доказательства, чтобы ты потом его мог восстановить если забудешь. А он учит доказательство в лоб.
Ну и че? Вопрос про матешу был. Это же анализ чистый
мимо Прошел курс механики
А тут пояснить нет?
Не понял твой вопрос. Приведи пример какой-нибудь
Какой самый лучший способ доказывать аксиому выбора?
Трансиндукцией
Точно, Генцен вроде так и доказывал аксиому выбора. Сейчас попробую.
Не получается что-то...
Ну тогда по старинке... Обычной индукцией
Как доказать, что каждая сюръективная функция имеет правую обратную?
Трансиндукцией
Это эквивалентно аксиоме выбора.
Как лучше доказывать, что декартово произведение непустых множеств не пусто?
Это аксиома, которую просто принимают
Я доказать хочу.
Тогда трансфинитную индукцию юзай
С помощью трансфинитной индукции (да и с обычной) вообще никак не получается.
А ты как доказывал?
Через Лемму Цорна
Хм... А как её саму доказать лучше?
в китайском антидемидовиче разбиралось гдето.... номер непомню
Никто не знает как доказывать существование сильно недостижимых кардиналов?
Каким образом они привели уравнение к этому виду? Там что-то типа фсу, но я понять не могу. Распишите более подробно все преобразования, кому не сложно
Заметь, что коэффициенты в уравнении стоят симметрично. Они поделили обе части уравнения на x^2 и перегруппировали. Если не понял, в первых скобках после преобразования возведи в квадрат x - 1/x и посмотри внимательно
Ясно, бьем себя по лбу. Спасибо!
Хочу повторить весь школьный курс математики, но не хочу читать школьные учебники. Посоветуйте, что-нибудь, чтобы были задачи. Остановился на Туманове и Сканави. Есть еще подобные?
Тебе их точно мало?
Есть лемма какая-нибудь про оптимальное количество дрочек в неделю?
>правую обратную
Это что?
Открытая проблема
Есть какие-то примерные догадки хотя бы насчёт того как её решать?
Дроча и анализируя.
А можно аксиому выбора простым перебором доказать?
>Если мы ограничимся рассмотрением только конечных семейств множеств, то утверждение аксиомы выбора может быть доказано исходя из других аксиом теории множеств[1] и не требует постулирования в качестве отдельной аксиомы
https://ru.wikipedia.org/wiki/Аксиома_выбора
Я хочу и для несчётных.
Начинай
Да, очень смешной мем, доказать недоказуемое. Долго ее срать будете?
лол, ее уже доказали в 30х
Помогите научиться переводить на православный пикрил ОП-поста.
Как-то не складываются у меня понятные куски в полностью осмысленные предложения.
Как-то не складываются у меня понятные куски в полностью осмысленные предложения.
Аксиомы ZFC?
Не обязательно только аксиомы. Как этот мат язык на русский переводить, чтоб читалось складно?
А то как нагородят по 3 вложенных скобки и прочей шняги, и как хочешь, так и разбирайся...
Наведи на истину, плеасе.
Они написаны очень естественно и так и читаются - слева направо. Если реально с этим проблемы, посмотри введение в Зориче, там автор даже приводит примеры, как читать такие конструкции
Ах ты мразь проклятая ,опять вылез, Зориче-даун?
Никогда не писал здесь про Зорича. Если ты не воюющий физмат-ребенок, предложи человеку лучший вариант, я не против
Непейвода - прикладная логика
Найти предел на бесконечности корень(x^2+x)-x
Почему мне говорят что предел равен 0.5, если он равен бесконечности?
А что не так с Зоричем? Один знакомый, который далек от математики сказал, что отличная книга, по ней матану даже обезьяну можно научить.
Он его не читал скорее всего.
кто тебе говорит? Покажи мне этого человека? Или что за книга?
Я нихуя не понимаю.
>Покажи мне этого человека?
Вольфрам, например
Потому что вот эта фраза
>бесконечности корень(x^2+x)-x
вводит в заблуждение и непонятно, что точно за выражение. Всегда точно пиши.
А так да, при x->infty sqrt(x^2+x)-x=1/2
Умножь
>sqrt(x^2+x)-x
на пикрилейтед, а дальше сам знаешь как.
Не знаю.
Где расовать такие пикчи и что использовать заместо CAS? Я сейчас максимой пользуюсь, ну у нее интерфейс запутанный, ящитаю.
Или после того как рационализировал предел поделить его на х и провести к пределу?
У Максимы еще норм интерфейс (с другой стороны, всё держится на командах). Можешь Математику попробовать. От себя скажу, что мне её mathematica, язык, не нравится.
>Где рисовать
http://www.texrendr.com/ я этим пользуюсь.
А здесь ты можешь прочитать как на latex писать выражения, ну и таблицы с символами для удобства:
https://en.wikipedia.org/wiki/List_of_mathematical_symbols
https://en.wikibooks.org/wiki/LaTeX/Mathematics
http://web.ift.uib.no/Teori/KURS/WRK/TeX/symALL.html
Да, делишь на x^2 и всё, дальше там всё очевидно будет.
Но у меня получилось такое уравнение. Зачем делить на квадрат? Под корнем чтобы поделить придется возводить икс в квадрат по любому.
Тьфу, я ошибся, да на x нужно (что-то я совсем уже). Но прежде нужно вынести x из под корня.
sqrt(x^2+x)+x = sqrt(x^2(1+1/x))+x = x*sqrt(1+1/x)+x
Минус на плюс у свободного x поменяй, а то ошибка.
И уже после дели на x.
БЛЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯТЬ Я ПОНЯЛ
Нестандартное число это число которое удовлетворяет неравенствам H>x, x∈ℝ, и 0<K<x, x∈ℝ.
Абстрактный объект который не используется непосредственно для счета, а только лишь для абстракции количества охуеть какого большого/неебацо маленького
Разве нельзя так поделить на икс, тупо введя икс делитель под корень с возведением в квадрат?
Можно. Выбирай как хочешь.
В какой аксиоматике проще всего доказывать аксиому выбора?
В любом трансиндукционном наборе аксиом
А зачем тогда бесконечно большие(малые)?
Приведи пример такого набора,, ссылку там или другое, что-то не верится...
сколько человек голосовало за каждый стоблик? я знаю, вы сможете посчитать
1 - 2
2 - 4
3 - 1
Вместо калечных пределов.
Функция называется непрерывной, если расстояние между двумя бесконечно близкими точками на ней бесконечно мало
>2a^2 = (24 - 2a)^2
>a^2 - 48a + 288 = 0
Это как? Я про свободный элемент.
Тебе стоит хотя бы сдать ЕГЭ выше 80 баллов и только после этого лезть со своими идеями. Математика это не мемы из МХК, это тяжелая и сложная наука.
> Тебе стоит хотя бы сдать ЕГЭ выше 80 баллов
Чет в голос ору с егэ-дауна.
>это тяжелая и сложная наука
ор выше гор
больно много сил надо на сложение или умножение
>сложение и умножение
Причём тут математика?
Если нет сложения или умножения, это не математика. Это -- философия.
>Гаусс
Как решать уравнение (x-vt)/v2=y?
y, v и t известны. Найти надо x.
Умножь обе части на v2
Черт, что-то тупанул. Неизвестно v, а x как раз известен. Извини.
Умножь обе части на v2
Сап, двач. Анон, проверь, правильно ли.
Задание: отметьте на числовой оси точки М(х), для которых: см. пик.
Правильно, но в б ты нарисовал неравенство, а в условии равенство
Умножь обе части на v2
Есть функция e^x
Нужно найти для нее ряд тейлора в точке один.
Берем функцию х+1, она сходится с нашей искомой в точке (0, 1).
Что делать дальше? Есть у меня х+1, что к ней дальше прибавлять?
Спасибо, сработало.
Раскладываешь тупо по определению ряда Тейлора
Такая длинная формула с производными от производных. Ты не умеешь по Тейлору раскладывать что ли? Если так, то в этом проблема при нахождении суммы рядов. Тейлор - это тема производных, а не рядов
Что-то я туплю.
Среднее арифметическое пяти чисел это 7. И первых четырех среди них это тоже семь. Какое пятое число? Как это решать?
Среднее арифметическое пяти чисел это 7. И первых четырех среди них это тоже семь. Какое пятое число? Как это решать?
Пятое число - 7.
Сумма первых четырёх будет 28, сумма пяти 35.
Сумма первых четырех это семь, среднее арифметическое их это семь или первые четрые числа это семь?
Ты шизик что ль? Среднее. арифметическое первых 4х равно 7.
х+y+z+a/4=7
(x+y+z+a+n)/5=7
n=35-x-y-z-a
Дальше сам
Как гипотезу Римана доказывать?
Как первую и вторую проблему Гильберта решать?
google: электромагнитная индукция
Но это же вроде физика? Мне математическими методами нужно.
Зачем? Куча интересных задач решается физическими методами
Например?
Математики унизят меня. Я хочу чисто математическими методами, ну или чтобы не заметно было.
В геометрии иногда задачу можно переформулировать для задачи в оптике, или в предположении, что какое-то геометрическое утверждение верно, можно построить бесконечный двигатель. Чисто хаки и трюки
Тогда через интеграл решай
А как лучше всего вычислять πk(S^n) для произвольных k и n?
Каким методом лучше проверять равенство произвольных вещественных чисел?
В какой системе аксиом?
NBG.
черещ парадокс рассела
сап, нужны видеоуроки ( хорошие, с подробным объяснением для дауничей, типа Timetostudy Сourses ) по интегралам с самого начала. желательно по русскому.
Так тебе по русскому или по интегралам?
по интегралам, ладно
По русскому, на интегралах.
Как доказывать, что аксиома выбора неверна?
Как получить Абелевскую премию?
За доказательство аксиомы выбора можно и Филдовскую получить. Или ты уже старый?
Обратной индукцией
А обычно люди помнят хоть что-то из доказательств в школе?
Я даже не помнил что они у нас были.
Я узнал о существовании доказательств, а следовательно и настоящей математике, где-то во втором семестре 11 класса и произошло это случайно
Аноны хелп! Какая есть теория по прямой, проходящей через центр вписанной в треугольник окружности и параллельной его стороне(треугольника)?
Почему 5-√16x9+5, тут квадратный корень берет с собой еще и умножение на девять? Кто и зачем такое придумал? И оно ограничено двумя операциями под корнем тип или чё?
Потому что умножение на 9 поместили под него.
Что за "поместили"?
Укажи, где начинается и заканчивается корень. А если его берут, значит он стоит под корнем.
Очевидно теория о центре вписанной окружности и параллельных прямых. Если тебе этого мало, то я подскажу, что особенного в центре вписанной окружности, теорема Фалеса.
Лемма Цорна.
А как доказать, что любая категория декартово замкнута?
На самом деле это ещё следует из леммы о том, что все группы абелевы.
Как гуглить истории типа "вкатился в математику вот так-то, до этого вообще не понимал ничего, а теперь я суперматематик 80 уровня"?
А ну очень просто. Обычно такие истории постят на сайтах и пабликах нормаьных вузов, если они иметются, потому что в математику можно вкатиться только через образование.
это недоказуемо
Окрестность.
Расскажите про примерный план изучения высшей математики, если на данный момент есть обрывочные знания из школьной программы - знаю что такое синус косинус логарифм, но совсем не умею в азы матанализа.
Почему?
Из-за парадокса Рассела
Совсем не понимаю тебя, причём тут парадокс Рассела?
Расскажите, пожалуйста, про о малое и О большое.
Я могу дать тебе определение, но оно будет не лучше, чем определение в википедии или в учебнике. Если ты никак не можешь понять, что это, попробуй в соответствующей главе Демидовича доказать пару равенств про О, либо вспомни пределы (О основывается на пределах, так что их знать надо)
На педивикии довольно невнятно, у Зорича немного мутно. Мне бы в такой, хз, конспективной форме, чтобы не вылетало из головы через день-другой.
Я просто постоянно путаюсь в записях, типа f = o(g) или f = o(1) и чем вообще O отличается от о.
Не, чел, тут педагог нужен. Для меня что википедия, что Зорич чистые и ясные, и по-другому и не объяснишь. Ты, видимо, не хочешь проходить матан, но для прожки нужны О. Такая запись постоянно встречается в матане, но если бы я не делал упражнения про О, я бы тоже не понял ничего
Да не, мне не для прожки, а именно для себя, чтобы ясности какой-то достичь с ними.
Из аксиомы выбора следует, что они равны.
Как можно доказать что существует сюръекция из одноэлементного множества в множество вещественных чисел?
А она существует?
Какие основные принципы математического мышления? Как думаете? Приведите пример внутреннего диалога.
Я думаю что существует. Только доказать не получается.
Как учить математику?
>Какие основные принципы математического мышления? Как думаете?
Что вообще под этим имеется ввиду?
Через прочтение доказательства аксиомы выбора.
АС - новый мемес /math?
Это серьёзный ответ был. Через неё можно многому научиться.
Как доказать, что существует бесконечное количество функций из натуральных чисел в пустое множество?
Для начала стоит нормально освоить школьную программу.
Че происходит, достаточно прочитать определения, чтобы понять что ее не существует, что за бред вы несете, откуда могла возникнуть такая мысль?
Берешь и делаешь.
Функция по определению - отображение в Вещественные числа. Как отображать в пустое множество не очень понятно вообще.
Алсо моча, почистите уже этого серуна, все засрал.
>Функция по определению - отображение в Вещественные числа.
Ты ебанутый?
>достаточно прочитать определения, чтобы понять что ее не существует
И почему её не существует? Докажи это.
Ты какой-то странный, не пиши больше.
>Как отображать в пустое множество не очень понятно вообще.
Берёшь элемент пустого множества и отображаешь в него. Что тут непонятного?
Читаем определение. Пусть существует, возмем эту сюръекцию, тут же получаем противорчеие, чтд.
Ты хуйню несёшь какую-то, причём тут вещественные числа вообще? Ты хочешь сказать, что в аксиоматиках где не существует вещественных чисел не существует и функций?
Аааааа, тогда извиняюсь, все ясно стало.
>тут же получаем противорчеие
Подробнее, почему мы его получаем? Это не доказательство.
Да, не существует. А ты видимо, просто путаешь функцию и отображение. Это не критическая ошибка, просто такая договоренность имеется.
А ты тогда ответь кто ты, откуда ты взял эту теорему и зачем пытаешься ее доказать.
>просто такая договоренность имеется
Среди тебя и твоих ебанутых друзей? Никогда не слышал про такую "договоренность", даже на русском.
Это просто лемма которую мне нужно срочно доказать. Я пытаюсь кое-что более интересное получить, но эту простую вещь никак не могу доказать.
Почему она ведёт к противоречию?
Что ясно стало?
>Среди тебя и твоих ебанутых друзей?
Мехмат так еще никто не называл. Но ок, если не нравится, давай будем считать что функция и отображение - синонимы.
Нененене. Кто ты? Откуда взял идею, которую доказываешь? Зачем ты ее доказываешь?
Ты автор поста ?
>Мехмат так еще никто не называл.
Я называю. Такими договорённостями только ебанутые будут страдать. Особенно если учитывать, что вещественных чисел не существует в любой нормальной аксиоматике.
>Кто ты?
Я уважаемый человек.
>Откуда взял идею, которую доказываешь?
Придумал недавно.
>Зачем ты ее доказываешь?
Из неё напрямую следует другая теорема которую я хочу доказать.
Ох, ну все все ты прав, я не прав, называть функцию отображением это очень тяжело, Зорич вообще поехавший. Че хотел то?
Ну допустим да.
>Зорич
Хуесос конченный, как и ты впрочем.
Я это понял уже все.
Кто ты? - образование, стаж математики, баллы ЕГЭ, все по чему я могу понять, что ты не ебанутый хипстер, который решил перед телочками понтоваться, а действительно математик, которому просто в голове что-то перемкнуло.
Лол, я просто подумал ты - зеленный, который глупость явную написал и решил поддержать шутку.
Почему на матемаче столько неадеквата? На дваче ж полно нормальных математиков, где они все?
Два года стаж, не учился в твоей стране, так что не знаю какие у меня были бы баллы ЕГЭ.
>которому просто в голове что-то перемкнуло.
Объясни подробнее.
>нормальных математиков
Сомневаюсь, что идиотов, у которых определение функции хоть где-то упоминает вещественные числа можно считать нормальными математиками.
>Два года стаж
Столько времени ты после вузика работал математиком? Или столько времени после школы ты по вечерам учил таблицу умножения?
>Столько времени ты после вузика работал математиком?
Нет, я имел ввиду стаж изучения.
Ты можешь доказательство написать? Я не понимаю почему это к противоречию ведёт.
Прости, но я не буду этого делать пока не пойму, что ты отучился хотя бы год на мат факе или имеешь знания эквивалентные этому.
Ты же говоришь, что это почти очевидно. Или ты не знаешь как формально это доказать?
Вот именно, это почти очевидно, да и писать надо не сильно много. Но где гарантия, что ты потом не придешь срать на доску со своим доквом Ферма или аксиомы выбора? Лучше уж я щас тебя на хуй пошлю, чем очередной шизик будет насиловать эту и без того опущенную борду.
>почти очевидно
просто очевидно
фикс
>да и писать надо не сильно много
Так в чём проблема? Твоё "очевидно" не является доказательством.
Я на самом деле почти полностью уверен, что это можно доказать. Так что я не верю тебе.
>что ты потом не придешь срать на доску
Ты и сам сейчас срёшь неплохо.
Ну ок, того чего я просил ты не принес, так что действительно, перестану срать здесь.
> Мехмат так еще никто не называл.
Бруквалуб, ето ты?
Чего ты от меня хочешь? Я не понимаю тебя. Ты истеричный какой-то.
>Бруквалуб
Впервые о таком слышу. Алсо это странно, огромное количество мехматских студентов тут сидит.
Историю о том, как ты отучился год на матфаке или получил знания эквивалентные этому. Достаточно рассказа, фоткаться с флажком в заднице не требую.
Не слушай
Какую-то чушь он несёт. Легко доказывается, что такая сюръекция существует, причём уникальная. Одноэлементое множество это начальный объект в категории множеств.
А ты мне нравишься.
пустое множество - начальный.
одноэлементное - терминальный.
Хоть вы тут все просто дурью маетесь, а мне бомбануло.
Ты видимо сам просто не знаешь как доказать это, вот и пытаешься тут своими "знаниями" похвастаться.
Это точно? Спасибо если это действительно так.
На самом деле в категории множеств начальный и терминальный объект совпадают. Доказывается довольно легко.
>Это точно?
Точно.
>Точно
Спасибо. Сейчас проверю ещё раз и напишу. Это единственное доказательство, или есть ещё?
> категории множеств начальный и терминальный объект совпадают
Что? Правда что ли?
>Это единственное доказательство, или есть ещё?
С точностью до изоморфизма. В категории доказательств оно является начальным объектом.
Правда. Доказывается довольно легко. Можно даже сказать, что доказательство тривиально.
В Set есть нулевой объект? {} изоморфно синглтону? Нахуй иди.
>В Set есть нулевой объект?
Да.
>изоморфно синглтону
Изоморфизм рефлексивен, так что да.
Ты ещё и издеваешься? Что такое быть терминальным или начальным объектом вообще? Как может быть пустое множество быть изоморфным любому непустому множеству? Что такое изоморфизм в Set?
>Ты ещё и издеваешься?
Что?
>Что такое быть терминальным или начальным объектом вообще?
У каждого объекта есть уникальный морфизм из начального, терминальный - начальный в C^op.
>Как может быть пустое множество быть изоморфным любому непустому множеству?
Никто этого и не утверждал. Если нулевой объект изоморфен синглтону, то очевидно, что и начальный и терминальный объект не являются пустыми множествами.
>Что такое изоморфизм в Set?
Биекция.
Среди дедов популярно выделять в классе всех отображений подклассы отображений R→R, R→Rn, Rm→R, Rm→Rn (m и n больше 1). Эти подклассы называются соответственно "числовая функция числового аргумента", "вектор-функция числового аргумента", "числовая функция векторного аргумента" и "вектор-функция векторного аргумента". Они ещё и словом "годограф" обожают пользоваться.
пилите перекат
Теоретико-множественные диды сразу нахуй идут.
Как доказать, что существует уникальный мономорфизм из объекта натуральных чисел в терминальный объект?
Нужно, чтобы это было верно в любом топосе.
Нужно, чтобы это было верно в любом топосе.
Давай так: терминальный объект - это такой объект Т категории С, что для любого объекта Х этой категории существует в точности один единственный морфизм f : X → T. В Cop терминальный объект - это начальный объект. Более конкретно, начальный объект категории С это такой объект S, что для любого объекта Х той же категории C существует в точности один морфизм f : S → X.
Смотрим, что у нас по этому поводу творится в Set. Из любого множества A существует ровно одно отображение f : A → {x}, где {x} множество, состоящее из единственного элемента х (для пущей экспрессии). Иными словами, |{x}||A| отображений.
Для любого множества A существует ровно одно отображение f : ∅ → A, так называемое пустое отображение. Других пустых множеств нет. Оно существует и единственно.
Далее, мы знаем, что если объект является и начальным, и терминальным одновременно, то его называют нулевым объектом. Такова тривиальная группа в Grp. Если в категории существует много терминальных (resp.начальных) объектов, то все они изоморфны. Ты говоришь, что в Set существует нулевой объект и более того, это {x} ≃ ∅. Покажи мне этот изоморфизм, биекцию между {x} и ∅, единственность морфизма f : {x} → Х для любого Х и отображение в ∅.
Напомнил, как в классе 7-8 на контрольной по физике было задание на график функции которое не мог решить. Пытался что-то придумать сам, почти "открыл" производную функции, но из-за мысли, что в математике нет термина "скорость" отбросил идею.
>пидорнутое издательство лань
если ты специально для траллинга взял эти пикчи, то окей
ну а если ты не знал, что это срань, которая в хуевейшем качестве с плывущими шрифтами на уебищной бумаге перепечатывает djvu-шки с либгена, то тебе стоит подредактировать пикчу, заменив 2 книжки на их оригиналы
Тогда проходи пределы и О-запись будет как родной язык. В Виноградове хорошо разобраны О, но пределы знать надо
Да и это доказуемо
>существует ровно одно отображение f : A → {x}
>Других пустых множеств нет. Оно существует
>и единственно
Доказательствa?
>{x} ≃ ∅
Никто этого не утверждал. {x} ≃ {x}, это единственный объект который и терминальный, и начальный.
А как доказать? Что-то не получается как мне сказали. Пытался доказать через то, что одноэлементное множество это начальный объект.
Это нельзя доказать на формальном языке, но можно доказать, что это доказуемо в принципе. Это, конечно, не эквивалентно доказательству, но почти эквивалентно аксиоме выбора
Если это сможешь доказать, то я не прав. Очевидно же.
Если докажу, ты мне отсосёшь?
Я не любитель таких вещей, а так бы отсосал конечно.
Помогите, плиз, с разобраться пикрил.
Знаю, что в результате получится f(x) = 0, f(x) = x - 1, f(x) = 1 - x, но не знаю, как к этому прийти. :c
Знаю, что в результате получится f(x) = 0, f(x) = x - 1, f(x) = 1 - x, но не знаю, как к этому прийти. :c
ты че сука, думаешь это смешно? Разбор этого задания ищи на сайте IMO
Вот ща как взял и начал в ангельский
Лучший способ начать.
ТАК ТАК ТАК, Все здравствуйте. Я знаю школьную программу, куда мне двигаться дальше в постижениях математики?! Интересует литература, порядок изучения, рекомендации.
http://ium.mccme.ru/old_courses.html
Открываешь любую ссылку и смотришь, что там написано под заголовком "Первый курс"
Я мимокрок и у меня маленький вопрос: как это равенство может быть верным, если мощность пустого множества равна нулю? Это очепятка?
Видимо, пустое множество в данном случае это элемент семейства. Чёт я тупанул, извините.
Ничего страшного.
Только что за хрень ты читаешь? Такое впечатление, что ещё немного и автор число сочетаний стал бы считать через пучки

































































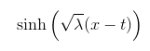
















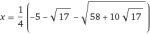

















Списки хорошей литературы:
http://pastebin.com/4iMjfWAf - Classic / http://pastebin.com/4FngRj6n - dxdy / http://4chan-science.wikia.com/wiki/Mathematics
Полезные ресурсы (OP):
http://gen.lib.rus.ec / http://mathprofi.net / http://math.stackexchange.com
Архив тредов:
https://pastebin.com/PMvY34XF