Дайте кто-нибудь задачник по анализу нормальный, Демидовича не предлагать.
>>203761
То, что такое конструктивно-приемлемые аксиомы теории множеств вопрос довольно туманный. Имеется более слабое и более ясное требование предикативности http://en.wikipedia.org/wiki/Impredicativity . Аксиома степени непредикативна т.к. она предполагает, что всевозможные подмножества данного множества уже известны и не могут быть построены в дальнейшем. Аксиомы выделения и замены непредикативны т.к. конкретный вид выделяемого множества зависит от от значений истинности некоторой формулы, которая может содержать кванторы по всей вселенной множеств и в рамках недостроенной вселенной невозможно узнать каково именно оно будет.
Стоит ли на раннем этапе изучения математики учить и вникать в аксиомы ZF? Или одной AC достаточно?
>>203796
Если ты не собираешься заниматься теорией множеств - ты их можешь даже не запоминать.
А вот если убрать аксиому бесконечности и заменить её отрицанием, все перечисленные аксиомы становятся предикативными. Даже аксиома выбора в финитистской конструктивной математике возможна.
Действительно ли математики склонны к аутизму? Как много у вас на потоках было ярко выраженных интровертов?
Как много в среднем на математических факультетах приличных вузов снг няшных тяночек? Какова тенденция изменения их количества с изменением меры математичности факультета? Что на счет разных стран? Имеет ли смысл съебать из украшки куда, чтобы получить больше приятных дамм и л'эди?
Есть вышка гуманитарной шараги.
28lvl
Знания довольно фрагментарные.
Ни одной статьи пока нет.
Но одна уже назревает.
Каковы шансы соискать ученую степень в математике (теория чисел)?
>>204104
Ну, скорее всего придется сдать академическую разницу. Шансы не нулевые. А нахуя тебе это? Идеи какие есть?
Посоны, просветите о тензорах. Кто такие, откуда берутся, зачем нужны? Почему старые добрые матрицы уже не в моде?
ананасы, как показать что число ab будет алгебраическим, если a - алгебраическое, а b - рациональное? корнем какого уравнения например оно является?
>>204117
>сдать академическую разницу
Эх, наверное, она будет большой, т.к. в моем ВУЗ'е было исключительно гуманитарное фуфло. Правда, есть академ. справка о завершении двух курсов в тех. ВУЗ'е.
>Шансы не нулевые
Это немного утешает.
>А нахуя тебе это? Идеи какие есть?
Хочу посвятить остаток жизни исследованиям. Параллельно мог бы работать за еду или преподавать. Идеи есть, но статус математика-любителя, боюсь, будет препоной на пути их распространения, да и никто всерьез воспринимать не будет математика-любителя, даже мама.
>>204150
>корнем какого уравнения например оно является?
Если a явл. решением уравнения P(x) = 0, то ab явл. решением xзнаменатель(b) степень полинома P(x) * P(x1/b) = 0.
>>204159
>xзнаменатель(b) степень полинома P(x) * P(x1/b) = 0.
ну а если у этого многочлена x будет в дробных степенях, как к целым перейти?
>>204157
> Идеи есть, но статус математика-любителя, боюсь, будет препоной на пути их распространения, да и никто всерьез воспринимать не будет математика-любителя, даже мама.
Сливай свои идеи кому-нибудь известному :3
>>204159
Как ты вообще заинтересовался математикой?
Что за няшка на пике?
>>204166
Ошибся. Не знаю как эту задачу решить пока... Возможно, потом к ней вернусь.
Мои мысли.
Корень любой степени из алгебраического числа также алгебраическое число: мы просто в полиноме аргумент возводим в эту степень.
Квадрат (а значит и 4, 8, ... степени) алгебраического числа также алгебраическое число. Доказать легко.
>>204221
>Как ты вообще заинтересовался математикой?
Теорема Ферма и советские книжки. В математике есть много задач, которые интригуют простой формулировкой. Например, явл. ли число Пи нормальным? Sum (1/n2) = Pi2/6, Sum (1/n4) = Pi4/90, а чему равно Sum (1/n3)? Эти задачи до сих пор не решены.
Не знаю, на форчане была популярна.
>>204224
Короче, попсоблядь еще одна, так бы и сказал. Что за советские книжки хоть?
>>204079
>Действительно ли математики склонны к аутизму?
Да
>>203761
почему считается, что континуальное множество нельзя представить при помощи двух счётных, когда любое число можно представить бесконечной дробью. Это же точней чем 0.(9)=1.(0) и всё такое!
>>204150
Очевидно. a^(1/n) алгебраическое, произведение алгебраических алгебраическое.
>>204289
>когда любое число можно представить бесконечной дробью
Множество бесконечных дробей несчётно.
>>204309
именно об этом я и сказал. берём два счётных множества, перемножаем наоборот (т.е. делим друг на друга), вуаля - получаем несчётное.
>>204327
что ты забыл в этом треде? а/b = a*(1/b)
или так:
а - счётное множество вида 1, 2, 3, 4,,,,n (n->inf)
b - счётное множество вида 1/1, 1/2, 1/3,,,,1/m (m->inf)\
а теперь расскажите будет ли иметь приоритет на это видение ушлый доцент, если начнёт на неё (увиденную на аиб) лепить своё имя, если его спалят дващерики из комиссии?
>>204328
Поздравляю, ты построил рациональные числа, по дороге попутав декартово произведение с числовым.
>>204335
>рациональные
implying иррациональное число не является бесконечной дробью
>>204335
Они не отличаются. Числовое произведение - это побочный эффект декартова произведения.
A x B = {(a, b) | a in A, b in B}
При взятии кардинализации уравнения имеем:
card(A) x card(B) = card({(a, b) | a in A, b in B}), которое при счетности множеств будет совпадать с натуральной алгеброй.
Учи матчасть.
Как найти наставника-математика, чтобы помог студенту обучиться? Преподаватель в университете сказал, что это будет лучше всего, но он этим заняться не может.
Просто чтения учебников и решения примеров не очень-то и хватает.
>>204414
Они отличаются типами, но это, скорее, философия. Алсо, слева у тебя должно быть card(A x B).
В любом случае, из декартова произведения двух копий натуральных чисел строится очевидная биекция в рациональные.
>>204416
>наставника
Ну если уровень мидихлориан у тебя в крови превышает 20000 единиц, то наставник сам найдет тебя.
>>204420
Бля. Ну такого уровня мидихлориан нет. Тогда придется искать учителя или даже МЕНТОРА.
Куда пропал рома михайлов?
>>204419
>очевидная биекция в рациональные.
и неочевидная в иррациональные неочевидна лишь по причине неспособности большинства человеков в бесконечные величины
>>204431
Ну давай, запили биекцию в иррациональные, Кантор ты комнатный.
>>204437
Виноват, не знал что такое биекция. Но зачем биекция? Произведение же!
>>204427
Серьёзно? Здесь что, и вправду когда-то был Рома Михайлов?
>>204475
Судя по жж, по крайней мере, раз был.
http://baaltii1.livejournal.com/312587.html
>>204472
Да, сижу, а что?
Заглянул под спойлер - получил красные способности на месяц
>>204468
Ты рассуждаешь о континууме, но не знаешь, что такое биекция.
Сдохни, мразь, я тебя презираю.
>>203761
>Почему аксиомы булеана, выделения и замены неконструктивны?
Неконструктивны в самом обычном смысле:
- аксиома булеана - не предоставляет алгоритма построения булеана, только логическое высказывание типа "для любого а найдётся b.." @ ГДЕ НАЙТИ ЕГО БЛЯТЬ??
- аксиома выделения - не сказано как именно мы можем перебрать элементы множества для построения нужного подмножества
- аксиома замены - опять не сказано как именно получить из всех элементов, которые существуют, подмножество
>>204507
Ты рассуждаешь о боге, но не знаешь что такое теодиция.
Сдохни, мразь, я тебя презираю. по сути-то тебе нечего возразить
Подскажите пожалуйста, что значит количество линий внутри кружков узловых точек у данной сети Петри?
И как правильно произносить? пЕтри или петрИ?
Матаны, предстоит весьма долгий перелёт. Хочу почитать что-нибудь более-менее занятное по истории математики, желательно охватывая 20й век. С математикой знаком хорошо.
>>204084
Оче мало. Меньше 10%, а няшных - ну хорошо если одна-две на курсе. И съебывать думаю толку нет. За тянками иди на филологию, хотя раз тебе это важно, то тебе даже там не дадут, лол.
>>204525
без аксиомы бесконечности - это уже детский садик у нас, а не математика
и она, кстати, конструктивна
>>204536
> она, кстати, конструктивна
Ну она, как вспомогательный инструмент для прочих аксиом, и ведёт к неконструктивности.
> без аксиомы бесконечности - это уже детский садик у нас, а не математика
http://www.google.de/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0CCkQFjAB&url=http%3A%2F%2Fwww.springer.com%2Fphilosophy%2Fepistemology%2Band%2Bphilosophy%2Bof%2Bscience%2Fbook%2F978-94-007-1346-8&ei=A9mvU8-0IKGr0gWDw4DQCQ&usg=AFQjCNE-I6__vRqATAAXcAynulY7eVOsiA&sig2=BmS7Gjqe2GEDdOSyWLbYgg&bvm=bv.69837884,d.bGE&cad=rja
>>204527
>Ты рассуждаешь о боге, но не знаешь что такое теодиция.
>Сдохни, мразь, я тебя презираю. по сути-то тебе нечего возразить
Строго говоря, предыдущий анон прав. У тебя есть интуитивное представление о боге, порождённое рассказами бабки у подъезда. Но у тебя нет и не может жить такого же интуитивного представления о континууме, потому что он определяется как "равномощный вещественным". Ты должен сначала знать, что такое равенство мощностей. Отсюда биекция.
>>204546
>Отсюда биекция
Разве я говорил, что мощность континуума равна мощности счётного множества? Я лишь продемонстрировал, что мощность континуума равна квадрату мощности счётного множества.
> представление о боге, порождённое рассказами бабки у подъезда
криптохристота, это ты?
>>204556
>что мощность континуума равна квадрату мощности счётного множества
Нихуя не равна. Мощность квадрата счётного множества равна мощности счётного множества. Биекцию можно установить, например, с помощью полинома Кантора:
f:N^2→N:f(n,m)=((n+m)^2+n+3m)/2
А теперь уёбуй.
>>204542
>http://www.google.de/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0CCkQFjAB&url=http%3A%2F%2Fwww.springer.com%2Fphilosophy%2Fepistemology%2Band%2Bphilosophy%2Bof%2Bscience%2Fbook%2F978-94-007-1346-8&ei=A9mvU8-0IKGr0gWDw4DQCQ&usg=AFQjCNE-I6__vRqATAAXcAynulY7eVOsiA&sig2=BmS7Gjqe2GEDdOSyWLbYgg&bvm=bv.69837884,d.bGE&cad=rja
спасибо за книгу, я наверное был неправ
>>204511
Блядская вакаба сожрала мой пост. Гори в аду, блядская макака!
Объясняю почему ты дебил:
Аксиома выделения: при заданных множестве и свойстве, возможно создать новое множество, помещая в него элементы данного множества по критерию обладания ими данным свойством.
Аксиома замены (на самом деле, подстановки, ты, я вижу, серьезным дерьмом быдлопереводчиков питаешься): при заданных формуле и множестве, при подстановке каждого элемента которого в формулу найдется элемент, делающий формулу истинной; возможно создать новое множество, отбирая из элементов, которые существуют, такие, для которых при подстановке в формулу найдется элемент из заданного множества, делающий формулу истинной.
>>204716
Хуй через плечо. Не прав он, вот что.
А тебе в ридонли на годок строго рекомендуется.
>>204818
Чё? Почему? И ты кстати даже не сказал, что он не так сказал.
>>204861
Ну что за даун. Я дал определения, в каждом из них, как видно, есть указание алгоритма словами русского языка. Даже имбецил может из этого написать строгий алгоритм.
>>204909
напиши мне давай алгоритм нахождения бозона хигса и придъяви его, сучечка
ведь козе понятно, что он существует, перебери и выбери, давай
>>204923
Для начала построй LHC, а дальше приходи за следующей инструкцией.
Вот такой вот интересный и простенький вопрос вам:
Х - 100 элемнтное множество. Каких подмножеств у него больше 43 элементных или 57?
>>203761
Аксиома булеана конструктивна для конечных множеств для конечных множеств есть алгоритм построения булеана, аксиомы выделения и замены - для счётных порядок, для перечисления элементов, можно перенести из N. В случае произвольных множеств, не обойтись без аксиом бесконечности и выбора. И всё это верно только с учетом того, что аксиома бесконечности конструктивной.
А вообще, эти разборки насчёт конструктивности и неконструктивности, сродни споров религиозных сектантов, которые сперва придумали каноны, а потом спорят по поводу того каким из этих канонов больше соответствует библия.
Оттого, конструктивны аксиомы или нет, ровным счетом ничего не меняется. Главное - непротиворечивость и всеобъемлемость.
>>204924
>Интересный для первокурсника шараги
Не благодари.
>>204935
А ты думаешь здесь кто-то есть кроме них? Я вот к примеру наткнулся в учебнике теории множеств Шеня. Просто показалось занятным, а ты столько говна сразу. Обижали в детстве?
>>204923
Ну что же ты за баран. В определениях уже написан алгоритм, он включен в определения, понимаешь, баранина?
Я сначала тебя покормил, но теперь ты кажешься совсем тупеньким. Это какой же там алгоритм описан в аксиомах? Ебанулся? Квантор сущестсвования понимаешь? Там, где идёт квантификация по произвольным множествам, алгоримт невозможен в принципе. Поэтому аксиомы неконструктивны для общих случаев. В частности при комбинации с аксиомой индуктивного множества.
>>204927
> Главное - непротиворечивость и всеобъемлемость.
Первое не доказать, второе весьма расплывчато. Конструктивная математика вполне всеобъемлюща для всех математических применений в мире, включая КТП и ОТО, и много больше.
>>204969
Лол, большая часть математики не имеет практических применений в мире. Приоритеты совсем другие. В первую очередь целостность и логичность внутренней структуры, и выявление закономерностей между различными областями математики. За практической пользой - к физикам.
>>204968
Во-первых, начинаются они с квантора всеобщности, во-вторых, после квантора существования идет описание свойства получаемого множества, из которого и следует алгоритм.
>>203761
Посоветуйте годной литературу про теорию групп и применения ее в физике.
>>204975
>большая часть математики не имеет практических применений в мире
а, вот и гуманитарии подтянулись
>>205016
Ладно, к сверхсчётно кардинальным множествам, может быть, алгоритма и нет. Тут я не подумал немного, да.
>>205028
> сверхсчётно кардинальным множествам
>>203761
При определении обратимого отображения F : S → S' необходимо существование G : S' → S так что F o G = I_s' и G o F = I_s.
Ослабляем определение требуя только G o F = I_s, тогда в силу того, что G функция, для любого y = F(x) существует G(y) = x так что (G o F)(x) = G(F(x)) = x.
То есть элементу для y из S' найдён x из S, который отобразится в y под F.
Почему F не обратимо? Почему нужно ещё ограничение F o G = I_s'?
>>205242
F:X*Y->X - проекция на первое слагаемого декартово прозиведения.
G:X->X*Y - естественное сложение X в декартово произведение.
FG=Id:X->X. Но GF<>Id:X*Y->X*Y
Ты, видать, линала даже не знаешь, ибо зная даже базовые вещи линала - становится очевидно, почему это не выполняется даже для линейных отображений.
>>205246
Ты не понял моего вопроса. Ты исходил из того что определение требует F o G = I_s' и G o F = I_s и показал пример который ему не удовлетворяет.
Я ослабил определение, потребовав только G o F = I_s и спрашиваю почему оно недостаточно для того чтобы утверждать, что у образа F существует прообраз. Да, нарушается сюръективность у F и тогда нарушается критерий обратимости (биективность). Но для любого x из S (F^-1 o F)(x) = F^-1(F(x)) = x где F^-1 равно G.
То есть под G элемент F(x) был обратно отображён в x.
Матаноны, проясните по хардкору - известная теорема Гёделя о неполноте вообще применима к чему-нибудь, кроме формальных арифметик? Как-то подзаебало, когда очередной диванный философ начинает "доказывать" с помощью этой теоремы существование (или отсутствие) бога и любую прочую хуиту.
>>205261
Сукпздц ты тупой школьник.
Я тебе привел ПРИМЕР, где ЭТОГО НЕДОСТАТОЧНО, что блять композиция в одном порядке - тождественный сука оператор.
Ты, долбаеба кусок, в первом сообщении спросил, почему этого недостаточно для сука ОБРАТИМОСТИ, я тебе, мудаку, привел контрпример.
Теперь ты, мудило, говоришь почему у образа нет прообраза, а потом сука сам пишешь, что нарушается сюръективность, да как блять пиздец ты вообще можешь подобное спиздануть и не ахуеть от того, какой ты мудило.
Сука, тупой школьник, я тебя ненавижу, мразь тупая.
Рассмотри блять любое да даже тривиальное накрытие или отображения вложения любых двух комплексных алгебр конечных различных степенией трансцдетности и пойми, что ты ссаный мудило.
Определение он ослабил, блять, да я тебе под ТВОЕ ОПРЕДЕЛЕНИЕ КОНТРПРИЕР СУКА ПРИВЕЛ.
Сдохни, мразь.
>>205291
>Я тебе привел ПРИМЕР, где ЭТОГО НЕДОСТАТОЧНО, что блять композиция в одном порядке - тождественный сука оператор.
Если ты про:
F:X*Y->X, G:X->X*Y
FG=Id:X->X. Но GF<>Id:X*Y->X*Y
То это не контрпример, потому здесь для любого элемента x из X (F o G)(x) = G^-1(G(x)) = x. Значит G^-1 способно отобразить G(x) в x.
>Теперь ты, мудило, говоришь почему у образа
Я этого не говорил. Я говорил, почему только G o F = I_s недостаточно для того чтобы утверждать, что для каждого y = F(x) из Im(F) : G(F(x)) = x.
нет прообраза, а потом сука сам пишешь, что нарушается сюръективность,
Сюрьективность => у образа есть прообраз. Обратное необязательно. Пример f : R → R вида f(x) = x². Здесь у любого f(x) из Im(f) есть прообраз (квадратный корень). Но f не сюръективна т.к. существует -1 в R для которого у f нет x так чтобы f(x) = -1. Если определить f : R+ → R+ то сюръективность будет.
>я тебе под ТВОЕ ОПРЕДЕЛЕНИЕ КОНТРПРИЕР СУКА ПРИВЕЛ.
Нет, ты привел контрпример не под мое определение.
>>205242
> Ослабляем определение требуя только G o F = I_s, тогда в силу того, что G функция, для любого y = F(x) существует G(y) = x так что (G o F)(x) = G(F(x)) = x.
> То есть элементу для y из S' найдён x из S, который отобразится в y под F.
> Почему F не обратимо? Почему нужно ещё ограничение F o G = I_s'?
>>205292
Сука, тупой долбаеб, ты блять в глаза долбишься, ТЫ САМ СУКА СПРОИЛ, ПОЧЕМУ ЭТО УСЛОВИЕ НЕДОСТАТОЧНО ДЛЯ ОБРАТИМОСТИ, А ТЕПЕРЬ ПОД ШКОНКУ, ШКОЛЬНИК.
> Я этого не говорил. Я говорил, почему только G o F = I_s недостаточно для того чтобы утверждать, что для каждого y = F(x) из Im(F) : G(F(x)) = x.
Сука, какой же ты долбаеб, из GF=Id сразу, СРАЗУ БЛЯТЬ СЛЕДУЕТ, что \forall y in Im F: y=F(x) => Gy = x тк Gy = GFx = Id x = x.
Пиздец, ты даун, советую больше не пытаться заниматься матемаикой, а перевестись на факультет менеджмента в твоей шараге.
>>205293
>из GF=Id сразу, СРАЗУ БЛЯТЬ СЛЕДУЕТ, что \forall y in Im F: y=F(x) => Gy = x тк Gy = GFx = Id x = x.
То есть F обратимое отображение, потому что y можно было перевести в x? И обратное к F это G (которое обозначим F^-1).
>>205242
Потому что обратная функция - это по определению биекция, в которой области отправления и прибытия поменялись друг с другом местами, говоря простым языком.
А если нет условия F o G = I_s', то область определения G может быть отличной от области значений F - например, первая является сверхмножеством второй.
Попробуй в качестве упражнения доказать следующую лемму:
f o g = e_X <-> surjective(f) & injective(g)
Её следствием является теорема, с которой ты испытываешь проблемы.
Ты уверен, что хочешь изучать математический анализ по этому учебнику? Не хочу задеть, но создается впечатление, что он для тебя сложноват. Может быть, что попроще попробуешь? Вот эту книжку в своё время обсуждали и многие сошлись на мнении, что это прекрасное пособие для детей, и не только: http://www.nostarch.com/mg_calculus.htm
А потом ты всегда к чему-нибудь более глубокому вернуться сможешь. Для эффективности всякой работы важна объективная оценка способностей.
>>205261
Несмотря на то, что обратное отображение также как и прообраз множества записывается с минус первой "степенью", это совершенно разные вещи. И несмотря на то, что твоя ошибка (точнее сказать, недосмотр) заключается не в этом, следует усвоить, что обратное отображение - это отображение, а прообраз отображения - это подмножество области определения отображения. Второе есть у всякого подмножества области прибытия всякой функции, а первое - лишь у биекций.
Попытайся записать математически строгие определения каждой категории самостоятельно.
>>204924
Очевидно, одинаковое количество. Спроси что-нибудь поинтереснее.
>>205320
Во первых благодарю за (относительно) адекватный ответ.
Во вторых дикие термины "область прибытия", "область отправления" в разговоре со мной применять не надо. Я знаю что такое домен и кодомен и чем они отличаются от прообраза и образа отображения.
В третьих последний абзац писать не было необходимости.
Теперь к частностям. Еще раз:
Определение: отображение f : S → S' называется обратимым если существует отображение g : S' → S что g o f = I_s. Отображение g мы назовем "обратным к f".
Покажем, что для любого элемента x ∈ S :
Если x отображен на y при помощи f
То y отображен на x при помощи g.
Пусть x ∈ S и y = f(x) ∈ Im(f). Поскольку g o f = I_s следовательно g(f(x)) = x <=> g(y) = x.
Значит y отображен на x при помощи g.
Полностью согласен, что при этом существует некоторое множество S'' = S' \ Im(f) на котором g может быть вообще не определена. И тогда если взять y ∈ S'' то не обязательно, что что существует x ∈ S так что f(x) = y. Следовательно нарушена сюръективность f.
Не понимаю как это все мешает тому что
(*) «Если x отображен на y при помощи f
То y ∈ Im(f) отображен на x при помощи g.»
А требование f o g = I_s на мой взгляд усиливает определение добавляя к f свойство сюръективности. Для чего? Для критерия обратимости? Тогда другой разговор. Но при этом следует учесть что биективность и обратимость «нетождественые» свойства. Для их «отождествления» требуется усилить определение добавив к нему f o g = I_s'.
>Её следствием является теорема, с которой ты испытываешь проблемы.
Я «испытываю проблемы» не с теоремой критерия обратимости а с определением обратимости посредством композиции. Из моего определения критерий не следует (о чем я говорил) но (*) выполняется.
>>205336
> Во вторых дикие термины "область прибытия", "область отправления" в разговоре со мной применять не надо
Чем это, позвольте, они дикие? Скорее уже дикие твои "домен" и "кодомен", пришедшие из английского языка. Второе слово вон фаерфокс даже красным подчеркивает.
> Полностью согласен, что при этом существует некоторое множество S'' = S' \ Im(f) на котором g может быть вообще не определена.
Ты совершенно меня не понял. Речь шла о том, что область значений F может быть подмножеством области определения G.
> Не понимаю как это все мешает тому что
> (*) «Если x отображен на y при помощи f
> То y ∈ Im(f) отображен на x при помощи g.»
Не мешает. Но я не зря указал определение обратного отображения:
> Потому что обратная функция - это по определению биекция, в которой области отправления и прибытия поменялись друг с другом местами, говоря простым языком.
Чтобы называть отображение обратным от данного, его область определения должна равняться области значений данного отображения.
> Из моего определения критерий не следует (о чем я говорил) но (*) выполняется.
Не рановато ли свои определения установившимся математическим понятиям давать? (*) - это не достаточное условие для взаимной обратимости.
Всё же какой учебник читаешь? Может быть, там просто объяснили плохо, такое часто бывает, все с этим сталкивались.
>>205425
>Чем это, позвольте, они дикие?
Дикие они тем, что не употребляются. Напиши ты "область определения", "область значений" - я бы тебя понял (так я тебя тоже понял, но глаз резануло).
>Скорее уже дикие твои "домен" и "кодомен", пришедшие из английского языка.
Да нет, тут в другом причина. Я думал, что co-domain (или «сообласть») это S', а не тождественен Im(f) = f(S). S' я называл сообластью, а f(S) образом.
>> Полностью согласен, что при этом существует некоторое множество S'' = S' \ Im(f) на котором g может быть вообще не определена.
>Ты совершенно меня не понял. Речь шла о том, что область значений F может быть подмножеством области определения G.
> Поскольку область значений f (или сообласть f, или codomain f) есть Im(f) = {y ∈ S' | ∃x ∈ S, f(x) = y} то "существует некоторое множество S'' = S' \ Im(f) на котором g может быть вообще не определена." логически эквивалентно тому что ты сказал.
>> Потому что обратная функция - это по определению биекция,
В третий раз: это не определение а критерий обратимости f. Определение дается при помощи композиций. Я определение ослабил - критерий нарушен.
>Чтобы называть отображение обратным от данного, его область определения должна равняться области значений данного отображения.
Области значений (то есть Im(f)) или множеству S'?
(*) - это не достаточное условие для взаимной обратимости.
Что есть "взаимная" обратимость и откуда она здесь внезапно появилась? Для обратимости f, что для меня эквивалентно (*) достаточно g o f = I_s. Биективности f нет (в четвертый раз) и я это прекрасно понимаю. Но y обратно в x перевести можно.
>>205425>>205441
Вы спорите об определениях. Причём оба они имеют право на жизнь. В абстрактной теории под обратимым отображением обычно понимается именно биекция, а понятие "область определения" вообще не водится. Если f: A -> B, то его обратное должно быть f-1: B -> A, т.е. должно быть определено в КАЖДОЙ точке B. Если ты сузишься на f(A) \in B, то инъективное отображение вполне себе станет обратимым, и формально f: A -> B и f: A -> f(A) - это таки РАЗНЫЕ отображения с разными свойствами - у одного есть обратное, а у другого нет. Каждое отображение может быть сделано сюръекцией путём сужения кодомена, и инъекцией - сужением домена (хотя тут уже аксиома выбора нужна).
В то же время иногда иметь отображения, определённые не всюду, довольно удобно, и в этом случае инъективности достаточно для существования обратного. К примеру, говорить о всюду определённом замкнутом операторе просто-напросто бессодержательно - он сразу окажется ограниченным, и ничего интересного мы в результате не получим.
>>205425
А ну все, то о чем я тут распинаюсь это "левая обратимость". Слово "взаимная" мне помогло. То есть тут обратимость это выполнение "левой" и "правой" обратимости. Что немедленно означает, что не только f но и g обратимо, и выполняется биективность (хотя этого никто не просил).
http://mathworld.wolfram.com/LeftInverse.html
ах сука вот ты где пидеры ебучии .сука папались наконец то учёные в рот мочёные. сука как я вас нинавижу умнеки хуевы выебоны
бля реально одного из вас встретить и по ебалу сьездить харашенько надо
хули вы такие выйобистые все а твари?
бля вот хуле я не понимаю на хуй что за хуйню вы тут пишити
бля давай реально забъйомся с кем нибуть я башню атшлифую атвечаю
>>205458
Ну давай розберемо по частинах, тобою написане)) Складається враження що ти реально контужений, ображений життям москаль)) Можу тобі і в очі сказати, готовий приїхати послухати?) Вся та хуйня тобою написана це просте піздабольство, рембо ти кімнатний)) від того що ти багато написав, життя твоє краще не стане)) піздіти не мішки перевертати, багато вас таких навесні відтануло)) Про таких як ти кажуть: Мама не хотіла, тато не намагався) Вслухайся в моє послання тобі <намагайся проаналізувати і зробити висновки для себе)
>>205443
> Причём оба они имеют право на жизнь
Not in math they haven't brah.
>>205441
> Дикие они тем, что не употребляются
В твоем учебнике? Это несколько самонадеянное определение дикости, не находишь?
> Я думал, что co-domain (или «сообласть») это S', а не тождественен Im(f) = f(S)
Я вижу ты запутался уже. Правильно ты думал, кодомен - это область прибытия, то есть третья буква, которая фигурирует в стандартной записи анализа вида "f : X -> Y".
>>205444
Надеюсь, ты понял свою ошибку? Ты употреблял именно "обратимое", "обратное" и так далее, что по умолчанию значит именно то, что я написал.
А учебник указать почему-то постеснялся.
Приведу статью из википедии: http://en.wikipedia.org/wiki/Inverse_function
>>205462
Да кокой смысл спорить с этим дауном, он даже что такое критерий не понимает. Кричит про какие-то определения, про нарушения критерия, кидается направо-налево модными словечками, вообще ахуеть.
Для мани:
В теоркате существование левого и правого обратного для стрелки - достаточно, чтобы она была эпиморфизмом и мономорфизмом, обратное неверно. Хотя индуцированные отображения на стрелках оказываются биекциями. Теперь маня, ты ахуешь и съебываешь в ахуе отсюда.
>>205462
>В твоем учебнике?
Нет.
>Это несколько самонадеянное определение дикости, не находишь?
Нет.
>> Я думал, что co-domain (или «сообласть») это S', а не тождественен Im(f) = f(S)
>Кодомен - это область прибытия, то есть третья буква, которая фигурирует в стандартной записи анализа вида "f : X -> Y".
Неверно. Берем f : R → R вида f(x) = x².
Ее кодомен или Im(F) есть R_≥0
Но "область прибытия" (прости господи) или "третья буква после стрелочки" есть R ≠ R_≥0. Неравенство двух этих множеств, надеюсь сам докажешь.
>Надеюсь, ты понял свою ошибку?
Да.
>Ты употреблял именно "обратимое", "обратное" и так далее, что по умолчанию значит именно то, что я написал.
Согласен. Вместо "областей прибытия" мог сказать и привести ссылку на left inverse, вместо траты постов и времени.
>>205468
Про теоркат я тебя не спрашивал, но раз уже ты завел речь: эпиморфизм и мономорфизм это названия сюръективного и инъективного гомоморфизма. Таким образом твои рассуждения верны для гомоморфизмов, но не для отображений.
>>205472
АХАХАХАХАХАХАХАХАХАХА, СУКПЗДЦ, УВЕЗИТЕ ЕГО УЖЕ НАХУЙ ОТСЮДА
>>205472
>эпиморфизм и мономорфизм это названия сюръективного и инъективного гомоморфизма
Это названия стрелки, сократимой справа и слева соответственно. В категории множеств стрелки - это отображения. И для них обратное как раз верно - стрелка, сократимая справа, имеет правый обратный. В других категориях это может быть не так.
Однако, какие воинствующие молодые люди.
>>205468
Копирую ссылку с моего предыдущего поста:
http://en.wikipedia.org/wiki/Inverse_function
>>205471
> Неверно.
http://en.wikipedia.org/wiki/Codomain
Резко у тебя вижу уверенности в себе прибавилось, стоило кому-то сверху с видом знающего человека со мной не согласиться.
Господа, я прочитал тред дважды, но как-то даже и не понял, о чём вы тут спорите и каковы позиции сторон. Объясните, пожалуйста.
>>205482
У меня все более крепнет желание начать изъясняться стилем этого >>205291 господина, но я этого делать не буду.
Итак: поскольку кодомен (или область значений) не есть образ f (пример с x ↦ x², где образ неравен области значений R). Следовательно:
>Речь шла о том, что область значений F может быть подмножеством области определения G.
Неверное утверждение т.к. область значений (не образ, а область значений) функции есть S' и оно не "может быть" а в точности равно области определения g (если g всюду определено, если нет то S' надмножество домена (области определения) g, а не подмножество.
>>205485
Путаница в терминах "образ функции" и "область значений" и непонимание определения "левой обратимости"
>>205485
Господа изволят сраться вокруг определения обратимости и обратной функции. Позиции сторон примечательны тем, что сути не понимает никто из них, иначе и срача бы не было.
Бля, это тупорылое школьное мудило все еще здесь.
Ладно.
F \in Hom(A,B) - морфизм между объектами A и B. Эквивалентная запись F:A->B
cod F := B
dom F := A
Сука, не образ, где ты блять образы нашел, мудило, где сука в категории может быть образ, что такое образ блять в категории, где объекты вполне упорядоченные множества, а стрелки - отношение "<". Где блять ты там сука образ найдешь? ГДЕ?
Тебя блять не удивило, что кообласть и область - категорные понятия, а СУКА ОБРАЗ МНОЖЕСТВЕННОЕ ПОНЯТИЕ? Пиздец.
С умным видом рассуждает о функциях, пишет кообласть, область, сука обратные функции рассмтривает, да ты мудило ни на что не годен в математике, тебе блять дорога на факультет почвоведения, пиздец.
Ты, мразота, знаешь, что такое критерий? С точки зрения матлога - это по сути ЭКВИВАЛЕНТНОЕ УТВЕРЖДЕНИЕ, с точки зрения теории, мы можем принять его за определение объекта, то есть сука, мы может сказать, что биективные морфизмы - и только они обратимы, а можем сказать, что обратимые - это когда есть стрелка, КОТОРАЯ ЕСТЬ ПРАВАЯ И ЛЕВАЯ ОБРАТНАЯ. ПОНЯТНО, МРАЗЬ?
Сдохни уже.
>>205490
Я просто проходил мимо и решительно ничего из того, что ты сказал, не понял — но я решил немного изменить твой пост. Итак...
F \in Hom(A,B) - морфизм между объектами A и B. Эквивалентная запись F:A->B
cod F := B
dom F := A
В данном случае нет никакого смысла говорить об образе: как можно рассматривать образ категории, если в категории объекты это вполне упорядоченные множества, а стрелки - отношение "<"? Каким образом, позвольте поинтересоваться, вы сможете найти тут образ?
Странно, что вас не удивило, что кообласть и область - это категорные понятия, а образ — множественное? Это ужасно!
Вы с видом знатока толкуете о функциях, употребляете такие слова, как "кообласть" и "область", рассматриваете обратные функции: но подобное, на мой взгляд, недостойно звания математика, и, возможно, лучшей судьбою для вас было бы сменить специальность и заняться, к примеру, почвоведением. Увы!
Осмелюсь спросить: знаете ли вы, что такое критерий? С точки зрения матлога - это по сути эквивалентное утверждение. С точки зрения теории мы можем принять его за определение объекта, то есть, уважаемый оппонент, мы может сказать, что это биективные морфизмы - и только они обратимы, а можем сказать, что обратимые - это когда есть стрелка, которая есть правая и левая обратная. Надеюсь, моё объяснение не слишком путано и я сумел донести до вас свою мысль.
Всех благ.
>>205490
Я не понимаю двух вещей: во-первых, почему ты истеришь и сыплешь оскорблениями, во-вторых, к чему ты вообще приплёл теоркат, который только вносит путаницу в сугубо теоретико-множественную постановку вопроса. Складывается впечатление, что ты просто очередной восторженный первокурсник, пытающийся самоутвердиться на сосаче путём употребления недавно услышанных умных слов. Это не /b/, своими дешёвыми выебонами ты тут никого не удивишь. Приходи, когда немного повзрослеешь, и не превращай тред в балаган.
мимопрокатился
>>205494
Эта мразь первая осмелилась бросаться теоркатовскими понятиями домена и кодомена, что вызывает во мне глубочайшие противоречия, зачем этот тупорылый школьник апеллируют такими понятиями, но не может понять простейшие вещи про функции.
А уж мой стиль общения - с подобными отбросами только так и приходится, ибо, как мы все смели заметить в этом итт треде, адекватные ответы подобной мрази не приводят к конструктивным результатам, только удары хлестом и объяснение, что это мрази место под шконкой, могут привести к результату: например, эта мразь может перестать как минимум постить сюда подобные вопросы.
А предположение, что я восторженный первокурсник - какое прекрасное предположение, жаль, что оно даже около не лежит.
>>205494
>к чему ты вообще приплёл теоркат
Стильно! Модно! Молодежно!
>>205497
К сожалению, этот постер имеет под собой хотя бы отчасти почву истины. Я как мог пытался понять его точку зрения и причину, по которой в неё никак не может попасть достаточно простой, в сущности свой, факт, но, видимо, поддержание приятельского стиля речи способствует пренебрежению.
Я всё таки спрошу очень настоятельно название учебника. Ты ведь пойми, пусть некоторые и пишут в раздраженном стиле, мы все сюда заходим в сущности, чтобы помогать обучающимся (в т.ч. самостоятельно), так что никто на самом деле против тебя ничего не имеет. А если ты укажешь на то самое заковыристое место, я, как минимум, приложу усилия, чтобы тебе хорошенько разъяснить, что имел в виду автор. И повторюсь: все, практически, рано или поздно прибегают к дополнительной или аналогичной литературе, здесь ничего такого нет. А пройти сначала по несколько менее глубокому пути - чтобы ты ни думал, очень продуктивное решение. А дальше уже можно расширять свой уже сложившийся математический кругозор. Я, если что, совершенно не шучу на счет той манги. У неё отличные обзоры и большинство математиков, которым приходилось её пролистать, весьма высокого о ней мнения.
>>205502
>Я как мог пытался понять его точку зрения
Я думал всё уже понятно. Ослабив определение обратимого отображения, я получил левообратимое отображение. Дальше шла путаница с понятиями "область значений" или "кодомен" (сейчас у него >>205497 опять пятиминутка начнётся) и "образ функции".
>пусть некоторые и пишут в раздраженном стиле,
Этих некоторых я игнорирую.
>>205510
Ах, верно, уже и забыл. Его пост заставил меня подумать, что ты еще на своём стоишь.
>>205510
> Ослабив определение обратимого отображения, я получил левообратимое отображение.
Блять, ебанный в рот, тупорылое мудило, ты получил, мразь ты тупая, инъективное отображение, определение он ослабил, вообще ахуеть.
Ты даже не понимаешь, что пишешь, я посмотрю. Сперва спрашивал про достаточность обратимости - сам не понял, что спросил, так стал всех обвинять, что тебя НИПАНИМАЮТ((99 Контрпример тебе привели, объяснили, что ты получишь только инъекцию, а второе тождество нужно для сюръекции. Ты даже не понял, что такое критерий. Знаешь, какого это видеть фразы в духе: "Почему это недостаточно для обратимости? Понятно, что критерий не выполнен, но почему этого недостаточно?", вот поэтому то блять я предлагаю тебе съебать из этого раздела в какой-нибудь /sn/ или /mg/, где сидят такие же поехавшие.
>>205514
Не понял, это аугментированная реальность на пике? Зоябись.
Вы чё, дебилы что ль?
почему так?
>>205721
Это философский вопрос или у тебя проблемы со школьным курсом?
>>205722
с подставлением в формулку у меня никогда проблем не было.
>>205723
ex — это просто по определению функция, которая всегда равна собственной производной.
А минус вылез наружу перед производной, потому что смена знака при иксе отражает график слева направо, т.е. рост превратился в убывание.
>>205721
Тебе доказать справедливость производной сложной функции?
>>205732
Образованец скатился до оскорблений, ожидаемо.
Не обращаем на него внимания, анончики, активней отвечаем.
>>205739
Надо всё-таки ужесточить модерацию в /sci. Задолбали.
>>205748
Типичный даун, неосиливший логику, спешите видеть.
сажи.
Монета падает орлом или решкой 50% на 50%. Я могу сделать ставку на любой бросок, на любую сторону, а могу не делать.
Мои шансы меняются как-то, если монетка на моих глазах упала 100 раз подряд решкой. Ну вроде как: "на 101-й вряд ли будет еще одна решка, можно на орла поставить."
>>205812
Если речь о идеальной монетке, то не зависит.
Но если подобное происходит в реальности, то, скорее всего, это какая-то жульническая монетка и тебя пытаются развести.
Посоны, недавно навернул курс по алгебраической топологии. Курс вроде норм.
Возник такой вопрос. Значит теперь я полчаса поебавшись с линейной алгеброй и теорией групп могу определить что в торе есть одна дырка или что то в этом роде. Но какие реальные приложения есть у гомологий и вообще алгебраической топологии в других областях? Какие задачи не решались без нее, а с ней на раз-два?
Няши, а можете доставить материал, где бы просто, понятно даже для тупых объяснялись пределы функций?
>>205871
Есть функция f, точка x_0 и число L.
У функции f существует предел L в x_0 если f(x) "способна быть сколь угодно близка к L".
Что значит "сколь угодно близка к L":
Это значит, что задав любое малое расстояние ε > 0, мы можем найти множество точек x рядом с x_0 так что для каждого x расстояние между f(x) и L будет меньше этого ε.
>>205868
В принципе неплохо знаю общую и алгебраическую топологию, но нигде и никогда применений не видел в реальных вещах. Ни в одном журнале, ни в одной конференции как минимум в таких областях как ТАУ, примат не видел ни единого применения. Возможно, робототехники что-то и применяют по части конфигурационных пространств.
Если же речь идёт о других областях чистой математики, то применения топологии и гомологической алгебры трудно недооценить -- они повсеместно.
Кстати, имей ввиду насчёт Вайлдбергера -- он придерживается весьма нестандартных взглядов на математику и весьма часто это проявляется в его лекциях. Ты, как новичок, можешь этого не заметить и принять за общепризнанный факт.
>>205945
> применения топологии и гомологической алгебры трудно недооценить -- они повсеместно.
ну хотя бы пару ярких примеров применения топологии
только не лемма про даму с собачкой - имхо неубедительная хуита
Посоны, посоветуйте ммаксимум доступное введение в теорию категорий, но чтобы лемма Йонеды была и все дела
только пидорского Авуди можете не предлагать, ему бы я в морду дал при встрече
>>205964
Чем тебе основная теорема алгебры неубедительна? Собственно, все простые доказательства у нее топологические. А на самом деле вообще все, т.к. от соображений непрерывности в каком-либо смысле там не убежать.
Из элементарного, например, что отображение из n-мерного диска в себя имеет неподвижную точку, теорема Борсука, теорема о причесывании ежа.
Теорема Безу является очевидной по модулю теории когомологий.
А вообще достаточно очевидно, что топологические инварианты важны и вылазят повсюду. Ну, т.е. когомологии де Рама дают сразу серьезную связь с анализом разным.
>>205976
> Маклейн
> доступное введение
попробуйте потоньше
>>205970
Ну если сам гуглом не умеешь пользоваться то например вот:
http://people.csail.mit.edu/shanir/publications/Topology.pdf
Сам охуел, когда увидел.
>>205975
> что отображение из n-мерного диска в себя имеет неподвижную точку, теорема Борсука, теорема о причесывании ежа.
у вас с википедией странное определение слова "применение", явно расходящееся с моим. По-моему "применение" топологии, это что-то, например теорема, не из топологии, которая использует теоремы из топологии, в качестве промежуточного шага
> Чем тебе основная теорема алгебры неубедительна?
Мы берем преобразование одного экстремально нетривиального контура в другой и в этом процессе должны пересечь ноль - ведь это же очевидно почему. На самом деле хочется сначала увидеть строгое доказательство (=на coq) что "оборотные числа" (забыл термин) контуров именно такие. А потом, что любое преобразование меняющее ОЧ, должно где то пересекать ноль.
Наверняка такое доказательство где то лежит, но не уверен что я пока смогу его переварить.
>>205978
Похоже на попытку совместить два баззворда, и не самую удачную в общем то
>>205979
В формулировках всех этих теорем не используется ничего из топологии. Наверняка они все были известны до появления топологии. Теорема о неподвижной точке уж точно, доказательство было вроде диким пиздецом.
Так оно строго совершенно, я сейчас могу изложить сходу немного по-другому, если слова фундаментальная группа и гомотопия не пугают.
>>205980
В общем то так можно сказать о любом исследовании совмещающем в себе несколько областей. Так что ничего информативного ты не сказал.
>>205976
>доступное введение
Попробуй Lavwere - Conceptual mathematics. Там понятие категории объясняется на простых примерах из жизни, как для младшеклассников, лол. На форчане ещё советовали Harold Simmons - An introduction to Category Theory, но пока не смотрел. Сам одно время задрачивал Awodey и Маклейна. Потом заебало, может позже вернусь.
Матаноны! Нужна помощь, вы сталкивались с задачей о глобальной оптимизации факторизируемых функций? Суть такова:
f(x1,x2) = psi(x1) * phi (x2)
допустим что можно найти глобальные максимумы и минимумы phi и psi. Надо найти глобальный минимум-максимум f по минимумам и максимумам (ну или другим особым точкам) функций-факторов.
>>206035
Возьми логарифм от обоих частей - справа получишь сумму логарифмов. Потом возьми градиент - получишь, что экстремум может быть когда обе функции экстремальны. Но видимо надо посмотреть отдельно что случается когда одна из них ноль (тогда логарифм бесконечен) - что-то вроде x1*x1*x2 - функция изрядно жопная.
Может ли кто-нибудь помогать иногда мне разбираться с кое-какими заданиями?
>>206062
Это одна из целей треда. Только помогать ≠ решать вместо тебя.
>>206065
Ни в коем случае. Просто детально обсудить теорию лучше и может дать какие-то подсказки лучше было бы лично, никогда не привыкну к доскам.
>>206070
Банальные основы 1-2 курсов. Анализ, топология, алгебра, теория чисел.
>>206071
Да пиши тут хули там. Мэйл/скайп геморно. А тут помогут думаю, если сам не смог. Для формул mathjax используй.
>>206072
Тут пошлют нахуй и скажут: "Хули ты долбоёб не понимаешь?"-, а спрашивать что-то более стыдно. Да и обсудить в чате как-то удобней.
>>206076
С такими соображениями мне тебя уже хочется послать нахуй. Блядь, тупишь - пиши в чем. Обзовут долбоебом, ну обзовут. Один обзовет, другой обзовет и объяснит, третий просто объяснит. Тебе важно понять тему или знать что ты долбоеб или не долбоеб.
Ломается тут как девочка.
>>206085
Я не ломаюсь, просто из чата как бы всегда выйти можно просто и потом зайти в новый, а тут-то мне еще сидеть после всего этого.
Ну и точно никогда не знаешь, действительно ли есть смысл то или иное задание писать, или никто не ответит и всё зря.
>>206124
> да и мне было бы просто удобней
Опять это кукареканье за "удобство". Да что ты, блядь, пиздишь? Ну каким в пизду образом чятик удобнее прекрасно функциональной доски? Что же вы, уёбки, так и не признаете, что вы просто закомплексованные аттеншнвхоры ёбаные, которые плохо переживают, когда кто-то их дебилами называет. Ну открою секрет: в чятике тебя тоже будут дебилом называть и тоже будут игнорировать, если посчитают вопрос слишком примитивным для их высокоорганизованного ума.
>>206128
Выйди из интернета, если собираешься кукарекать за субъективное понятия удобности персонально для меня, тем более я ищу только одного человека, который бы не послал нахуй при элементарном вопросе.
>>206139
Один человек регулярно тебе время посвящать не станет, и что если тот, кто будет с тобой сюсюкаться чаще всего, будет заодно называть тебя хуесосом?
>>205974
А чего это ты на Аводи распизделся? Ниасилил?
Эй, хватит этого нытика кормить.
По поводу гомологической алгебры. Погугли, была библиотека на крестах, в которой триангуляция и вычисление гомологий было закодено. Может, в этом направлении и до какого-то применения можно докопаться.
>>206171
Говно твой Аводий
И библиотеку свою на крестах можешь себе в сраку засунуть. Она мне нахуй не сдалась
>>206177
Я одного не могу понять. Если ты знаешь о лемме Йонеды откуда-то, а еще зачем-то она тебе нужна, то почему Маклейн кажется сложным?
Кстати, мне кто-нибудь может пояснить суть леммы Йонеды (или сказать где она хорошо объяснена, или указать на показательное использование). Читал года полтора назад в Маклейне, в доказательстве разобрался, но как-то не проникся, почему это очень важная и концептуальная вещью
>>206190
http://en.wikipedia.org/wiki/Yoneda_lemma
В Generalities немного написано.
Анон, посоветуй хороший учебник для изучения основ топологии. С уклоном в алгебру желательно. Хотелось бы, чтобы изначально все базовые топологические понятия давались в алгебраических терминах. инбф: бурбаки
>>206740
Тебе нужна топология или основы топологии?
Основы топологии - это то, на чём стоит топология. Логика всякая, философия.
>>206798
>Основы топологии - это то, на чём стоит топология.
Долбоёб, то, на чём стоит - это основания.
>>206177
Ох-хо-хо, как мы распизделись!
Говно ты, а не Аводи. А библиотеку я засуну твоей мамаше в дупло, ублюдок херов.
На хуй отсюда вали, чмошник.
>>206846
Сука, ты тут дохуя блатной, что ли? Такие долго воют потом как в ебальце пропишешь при встрече. Ты следи за ротешником, хуесосер мамкин. А Аводи сраное говно, точка.
>>206884
А паспорт тебе не сфотографировать, хуй дроченый? Если реально хочешь стрелку, пили любое время практически любое место, питер(хуитер).
>>206904
Гостиный двор, у аптеки, сегодня в 23.00.
Я: рост примерно 190, вес около 100, одет буду в спортивные штаны тёмно-синего цвета без рисунка и олимпийку тёмно-синюю с тремя белыми полосами по рукавам, в чёрной кепке. Жду.
>>206923
> Гостиный двор, у аптеки
Охуеть теперь. Пили бля ссылку на гуглмапах.
> рост примерно 190, вес около 100
Ты пёрышки взъерохивать не торопись, а то стыдно будет, как предстанешь во всей красе в ирл.
>>206930
Ну хули же ты не пришёл, фраер? В пузырёк полез?
>>206923
>рост примерно 190, вес около 100
мушку то спили, на всякий случай.
Реально ли самому выучить теорию групп, топологию и функан до уровня решения задач?
>>206981
Ты хули не пришёл блять? Я пришёл и твою мамку выебал перед всем питером.
>>207005
Нет, тебе обязательно нужен посредник, переписывающий выжимки с учебника на доску, чтобы ты их потом переписал в тетрадку; и вот только по такой тетрадке и можно чему-то научиться, иначе никак.
>>207014
И что мне, у тетрадки спрашивать, как вот эту задачу решить и почему у меня ответ не сходится?
>>206981
Эх блядь знал же, что пидорок зассыт. Очко сжалось, да? Или изначально не планировал, просто патролить))) решил? Ну всё, чёртик, теперь даже не высовывайся. Ты опущенец обоссаный теперь официально.
>>207035
Так лутше.
>>207114
>безвкусность
>близорукость
Тебя спросить забыл.
> mfw reading this thread
> imagining nerdish shivering basement dwellers squeezing fists and expecting a virtual fight
>>207200
Американец дохуя? Так иди бля бургеры жуй на форчане, хуила. Тут таких не любят, лалка, лучше пиздуй пока ротешник не обоссали.
Самый охуенный тред за джва года.
пидарасы бля я всегда знал.каждому-бы уибал из вас
Почему такой могучий человечище, как Колмогоров, в своём учебнике для 10-11 классов ни слова не сказал про комплексные числа, не раскрыл тему пределов и даже про хорошо раскрытое применение в науке дифференциального и интегрального исчислений так мало написал?
>>207357
Вопрос не в Колмогорове, а в школьниках. Его учебник и так зачастую ругают за излишнюю переусложнённость.
>>207357
Потому что всё это не нужно. 99% россиян достаточно умения складывать числа в пределах тысячи.
>>207360
Идея не новая. Гиммлер в школах на славянской территории хотел счет до ста, умножение запретить и немножко немецкого чтобы понимали приказы.
Анончики посоветуйте пожалуйста книжку по высшей математике написанную не профессорами для профессоров, а людьми (или профессорами) для людей, чтобы понятно всё объяснено было. Я не школота и не студентота, просто хикки которому понравилась идея делать открытия на кончике пера.
>>207409
Мамфорд "Красная книга"
Скопировал свой вопрос.
>>207272
> Науканы, скажите, зачем гениальному математику лаборатория? Может ли он обойтись без неё и работать дома? Что нужно для того, чтобы его решения приняли к рассмотрению в научном сообществе? Тот же Перельман в лаборатории работал над гипотезой Пуанкаре и вообще в тусовке научной был.
>>207409
Двухтомник Клейна "Элементарная математика с точки зрения высшей"
>>203761
Хочу найти алгебраическую формулу для вычисления факториала. Нашёл первые 8 полиномов, значения которых совпадают с соответствующими значениями факториала. Вот последний найденный: p(x!) = -x^7 - x^6 - x^5 + x^4 - x^3 - x^2 + 2x + 1. Совпадают первые восемь значений. То есть p(x) = x!; [1, 8]; Вопрос, как можно вычислить общую формулу?
>>207526
Твоя формула - разложение гамма-функции в ряд Тейлора, и в ней бесконечно много членов.
>>207528
Воу! Получается точно значение факториала по ней не вычислить? А чем же тогда является мой полином?
>>207529
Полиномом, который совпадает с соответствующими значениями факториала. Полиномиальной формулы нет чисто из аналитических соображений: факториал растёт гораздо быстрее любого полинома.
>>207526
Факториал приближенно считают по формуле Стирлинга (см Вики). Полином степени эн который проходит через эн точек нарисовать всегда можно, но для гамма-функции (факториала) хорошего (сходящегося от 0 до бесконечности) разложения в ряд Тейлора не будет - у гаммы полюсы в 0, -1, -2 итд. Попробуй нарисовать твой полином - возможно получится гнусная осциллирующая хрень вместо гладкой кривой.
>>207535
Сукпздц, че несешь. Имплаинг, что осцилирующий полином(ЧТО БЛЯТЬ) не гладкая кривая.
Чепушок, приходи снова, когда выучишь определение гладкого многообразия.
>>207540
Чмо ты - я чуваку поясняю, что он в натуре увидит на картинке, а не то, что называется гладким, а что лохматым. Многообразием же называют график разве законченные матпидоры. Это все равно что кота звать плотоядным млекопитающим.
>>207543
Может ты еще спизданешь, что называть проективным пространством простой спектр проективного кольца с индуцированной топологией - это тоже самое, что называть человека - обезьяной? Пиздец дебил.
>>207551
Школьник порвался, несите следующего.
>>207540
> Сукпздц
> Имплаинг
> Чепушок
> Анимешная картинка
Уёбывай отсюда.
>>207526
>p(x!) = -x^7 - x^6 - x^5 + x^4 - x^3 - x^2 + 2x + 1
Не верно для натуральных x.
>Совпадают первые восемь значений. То есть p(x) = x!; [1, 8]
Первые восемь значений p(x) (x = 1,2,..,8): -1, -215, -3107, -21319, -96389, -333311, -955975, -2388527.
>>207571
Очередной школьник-неоилятор подтянулся))
>Не верно для натуральных x
Сам написал ерунду. В общем, ты поясни как ты получил свой полином лучше.
>>207447
Можешь пояснить на примере, что алгебраическая геометрия нужна для вычислений? Ведь есть же алгебра и комбинаторика.
>>207576
Толсто, ну ладно, покормлю.
Понимаешь, что твой вопрос имеет столько же смысла, как и вопрос "Можешь пояснить на примере, что физика нужна для вычислений? Есть же биология и химия".
Ты сравниваешь разделы с разными целями и мотировками. Да и вообще, что за раздел такой "алгебра"? Алг. геом туда относится, например.(Ну коммутативная алгебра то точно).
А комбинаторика - это вообще пушка, каждый второй неосиливший математику, но очень желающий причислить себя к математике - начинает "изучать" комбинаторику и прочую хуиту-числодробильню. Не надо так.
А пример, где алг. геом./комм. алгебра нужны для вычислений:
В книжке "идеалы, многообразия и алгоритмы" есть примеры, где это в робототехнике используют.
>>207578
Просто меня интересуют символьные вычисления. Поэтому я знаю, от изучения математического анализа будет толк, от комбинаторики - будет толк, от булевой алгебры - будет толк, от абстрактной алгебры - вероятно, тоже будет толк. А вот алгебраическая геометрия для меня что-то мутное, не понимаю зачем нужны кривые, зачем находить на них какие-то точки, чтобы решить дифференциальное уравнение. Поэтому для меня это "теория категорий" - математика в себе.
>Да и вообще, что за раздел такой "алгебра"?
Абстр. алгебра: поля, группы, кольца и т.п.
>А комбинаторика - это вообще пушка, каждый второй неосиливший математику, но очень желающий причислить себя к математике - начинает "изучать" комбинаторику и прочую хуиту-числодробильню. Не надо так.
Аналитическую комбинаторику и теорию чисел называть хуиту-числодробильней - не надо так.
>А пример, где алг. геом./комм. алгебра нужны для вычислений:
В книжке "идеалы, многообразия и алгоритмы" есть примеры, где это в робототехнике используют.
Спасибо на этом. Хотя я был бы рад более простому единичному примеру, такому как пикрилейтед, который я не знаю как решить без знаний математического анализа.
>>207573
Кто на пике?
>>207575
Вычисляю по своей программе. Вбиваешь туда значения полинома в n точках: p(0), p(1), ... , p(n-1), а она выводит тебе формулу этого полинома. Но! Для факториала по моей программе у меня не получилось подобрать такой полином, чтобы он соответствовал значениям n! от одного до 8. Я тут посчитал, если задавать значения от 1 до 5 уже получается какая-то ерунда. От 1 до 4 ещё можно подобрать, а вот для пяти уже нет. Наверное это из-за того что факториал уж очень быстро набирает рост.
>>207591
>"теория категорий" - математика в себе.
Ты это зря. У теории категорий большой потенциал. Возможность устанавливать соответствия между различными областями математики и науки неоценима. В этом направлении уже делаются шаги. Посмотри книгу Спивака (arxiv.org/abs/1302.6946), например, он приводит примеры применения теории категорий в биологии и физике.
>>207591
>Поэтому для меня это "теория категорий" - математика в себе.
Самое смешное, что теория категорий применяется во вполне прикладных задачах; с алгебраической геометрией я не знаком, но подозреваю, что и у неё есть "вычислительные" приложения. На самом деле наличие разнообразных приложений у сильно абстрактных областей математики вполне ожидаемо т.к. удачные абстрактные конструкции могут проявляться в сильно различных областях.
Отправил жалобу на аватакрофага.
>>207610
Мария, лишился с ней девственности.
Интерпол. полином для люб. функции строится как два пальца обоссать, гугли интепол. полином Лагранжа, смотри пикрилейтед для твоего случая.
>>207591
Раз тебя интересуют символьные вычисления: базис Гребнера для идеалов(напрямую связан с алг. гемом, ибо как минимум позволяет находить решения полиномиальных систем уравнений) и алгоритм Бухенбергера для его построения - позволяют алгоритмиески определять принадлежность многочлена идеалу.
+последнее время модно в алгоритмах/алг. сложности говорить о алгебраическом многообразии алгоритмов.
>>207610
Ебать дебил, любой многочлен степени n однозначно определяется n+1 точкой.
>>207638
Какой ты дерзкий)) Поссал на дебила))
Такой вопрос. Можно ли из трёх аксиом группы (ассоциативность, наличие единичного и обратного элемента) вывести тот факт, что для каждого a и b принадлежащих группе, следует что их произведение (бинарная операция группы) тоже принадлежала группе (т.е. что группа замкнута)?
>>207775
Бинарная операция на группе G есть функция G✕G→G. Очевидно, что операция не может быть незамкнутой.
>>207719
>people die if they are killed
bitch please
Ублюдок, ты доиграешься. Прекращай аватаркофажить в тематике.
>>207810
Удачки забанить динамику на несколько милионников, лол.
>>207810
Ахах)) Мань ты чего)) Ты че такой грустный)) Хуй что ли попался невкусный)) Ахах))
>>207775
Пусть Z - группа целых чисел по сложению.
Подмножество {-1,0,1} - удоволетворяет твоим условиям, очевидно, незамкнуто.
Как в аксиоматике тервера объясняется сущность случайного события? Что такое именно "выпадение" некоего исхода? Что именно такое случайность? С сигма-алгеброй множеств ясно, но как понять само событие, скажем, происходящее во времени или как-то абстрактно?
>>208649
Такие тонкости обычно не рассматриваются. Ничто не мешает тебе сделать свою теорию и извлечь какие-то следствия.
>>208522
Поссал на дебила. Может ты еще в когерентных схемах сущность искать будешь? Пиздец дебил.
>>203761
Есть ли годные книги по матану inb4 матан is not calculus, алгебре и прочей топологии на английском, но не переведенные на русский? Или все самое годное переведено и/или изначально было на русском?
>>208674
Хуй твоей мамаши.
*мог бы
fix
>Или все самое годное переведено и/или изначально было на русском?
Лол.
Ну есть двухтомник Тао по анализу, например.
>>208686
Какие? Интересуют именно маст рид, но которых нет на русском.
>>208714
Ты заебал. Если интересует какая-то конкретная область - спрашивай, если нет - пиздуй на форчановский sci и читай sticky.
Колмогоров - уебан тупой.
>>208738
Высокомерные выблядки-олололгении не нужны. Так пойдет?
>>208736
>Если интересует какая-то конкретная область - спрашивай
Комплексный анализ. Но я и реального толком не знаю. Что посоветуешь? Чтобы без утомительных задротств по несколько страниц, чтоб по хардкору, короче. Читал давно Рудина "Основы анализа" в библиотеке - времени оценить особо не было, но понравилось, просто и доходчиво, правда, как мне показалось, не основательно, по вершкам, так сказать. А вот эта книга не слишком ли стара?
http://www.amazon.com/Complex-Analysis-International-Applied-Mathematics/dp/0070542341/ref=sr_1_1?s=books&ie=UTF8&qid=1406656046&sr=1-1&keywords=rudin+real+and+complex+analysis
А то, боюсь, в ней не затронуты современные реалии. Сейчас теорию категорию задрачивают, я слышал, типа современный и многообещающий подход. Вот, хотелось бы услышать менение русского математика:3 Русские математики одни из сильнейших.
>>208736
Ты зачем такой агрессивный? Неужели ты столько охуенных книг знаешь, что их все писать очень проблематично.
А по делу, от школьных до 1 курса универа матан, ангем, алгебра, матлогига, дрыскетка, приложения математики в информатике etc ибо я школьник, который решил убить двух зайцев - подтянуть английский и подготовиться немного к универу. Если будут снабжены годными задачами, так вообще очень счастлив.
Для большей ясности хотел бы уточнить, комплексный анализ интересен с точки зрения следующего вопроса. А почему он так необходим? Чем он крут, короче? Обычного мало что ли? Комплексные числа нужны, но вот переход к комплексной переменной зачем вообще нужен? Чебышев, например, недолюбливал комплексный анализ. Многие считают, что именно по этой причине он не получил известные уравнения Римана из теории чисел и не сформулировал гипотезу дзета-функции Римана.
>>208821-кун
>>208825
Просто пиздец. Откуда вас столько дебилов, не могущих в абстрактное, математическое мышление?
Советую перестать пытаться изучать математику и вылететь поскорей из своей шаражки.
Понимаешь, дебил, ты рассуждаешь о вещах, которые не понимаешь, но делаешь умный-умный вид, что понимаешь, что говоришь. О вещах, которые не достижимы твоим скудным умишком, но тебе почему-то хочется до них достучаться.
Вам, дебилам, бесполезно объяснять, что такое комплексное многообразие, комплексификация пространства и етц.
Знаешь почему в коммутативной алгебре и алгебраической геометрии рассматриваются только поле комплексных чисел? Да потому, что оно самое простое для изучения, все самые entry-level важные результаты даются в комплексном случае, в этих случаях максимальный спектр кольца в топологии Зарисского оказывается гомеоморфен алгебраическому многообразию.
Но ты ведь тупой, тебе даже этого не понять.
Вообще ахуеть, обычного анализа мала, да я этот ваш обычный анализ в рот ебал, петух блядь!
Может ты еще спизданешь, что топология не нужна? Что, на вещественное прямой топологии не хватает? Пиздец дебил.
>>208836
Ты мне нравишься, ты очень много знаешь. Слушай, помоги, пожалуйста лашку как мне. Я вижу ты шаришь в теме и готов даже выслать тебе мат.помощь, если ты мне поможешь решить одну простенькую задачку по матеше в школе. Вопрос вообще пустячный должен быть для такого гуру как ты.
Можна ли запoлнить 7-мерное пространство равными 7-мерными гиперкубами так, чтобы никaкие два гипeркуба не имeли целой общей 6-мерной гипeрграни?
>>208836
>Вам, дебилам, бесполезно объяснять, что такое комплексное многообразие
Никогда не понимал подобные понятия и считаю, что другие только делают вид, что понимают.
Цитирую Википедию
>Многообра́зие (топологическое многообразие) — хаусдорфово топологическое пространство...
>Топологи́ческое простра́нство — множество с дополнительной структурой определённого типа (так называемой топологией)
>Пара (X,\;\mathcal{T}) называется топологическим пространством.
Стоп, сначала топологическое пространство определяется как множество, ограниченное определенными свойствами. Теперь вдруг оно становится парой двух множеств! При этом что такое пара никакого объяснения не дается. Ну пара и пара, а как с ней работать - догадайся сам.
>>208842
>Гипотеза Келлера.
Пошел нахуй.
>>208844
> Стоп, сначала топологическое пространство определяется как множество, ограниченное определенными свойствами. Теперь вдруг оно становится парой двух множеств! При этом что такое пара никакого объяснения не дается. Ну пара и пара, а как с ней работать - догадайся сам.
Пиздец дебил, ты даже этого понять не можешь, но говоришь мне про:
>Никогда не понимал
Впрочем, ты тут сам признал, что тупой и не понимаешь.
Утенок, блять.
>>208844
Топология != топология. Первое - область математики, второе - математическая структура. И вообще перестань читать статьи по математике в рузьке википедии, они сделаны на отъебись. Читай ту же тему, только на английском.
>>208845
Ну пля((( Это ваще чет неправильный ответ( Там да или нет должно быть вроде, ну и доказательство. Ты че, решить что ле не можешь? Я тебе 1000 рублей скину еси сюда решение правильное выложешь.
А еще моему братику младшему задали (у нас с ним одна училка по матеше), это ваще вроде как орех такой гуру как ты должен щелкнуть:
сущeствует ли прoстая группa, кoторая нe являeтся трансфинитнo свeрхпростой?
заранее спасиба
А, хотя, виноват, определение пары все-таки дано.
>>208844-кун
>>208848
> сущeствует ли прoстая группa, кoторая нe являeтся трансфинитнo свeрхпростой
Нет. Доказательство у меня есть, но размер этого поля для ввода не позволяет мне его написать. Так брату и скажи.
>>208850
О класс!! а чо там с кубами? семимерными? там ваще как ситуация складываеца вцелом?
>>208850
Братишка хочит еще вопрос маленький задать пока гуру здесь. перидаю вопрос почти без изменений... слово в слово
"видил ли ты график функции дзета-функцыи? навскидку не помнишь, там все нетривиальные нули лежат на Re(z)=1/2 или не все?"
у нас просто типа контры завтра, паэтому училка дала задачи подготовица. заебала уже((((
>>208852
Я построил эти кубы в анале твоей мамашы, но амал твоей мамаши слишком велик, чтобы вместить его на страницы сосача, петух.
>>208855
Чот мне кажеца ты нихуя не математик на пездабол обычный
>>208836
>все самые entry-level важные результаты
Какие важные результаты? Что какая-то там херня гомеоморфна другой херне? А этот важный результат важен, чтобы узнать о какой-то хуйне из спектра кольца чего-то там... Пиздец, вы сами от себя просто кайфуете и срете там, где люди реально занимаются наукой. Тонны мукулатуры, блядь, которую никто никода не прочитает. Короче, просто паразиты. Ньютону не нужны были обоснования аппарата, что он придумал вместе с Лейбницем. Он просто работал. Вся физика сейчас описывается диффурами. Вы же занимаетесь абстрактной херней, которая также полезна для практической жизни как поэмы Шекспира, блядь.
>>208859
> Вся физика сейчас описывается диффурами.
Ахахахахахахаха, бля, унесите этого поехавшего.
Так ты значит и физику неосилил, ахахахахахахахахахаха.
Теория схем и квантовые группы - аппарат теорфиза, теория симметрий, суперсимметрий, и етц.
А ты со своей вычислительной парашей 18 века пройди нахуй.
Алг. геом, комм. алгебра, теория схем, квантовые группы, некоммутативная геометрия, гомологическая и гомотопическая алгебра и с топологией - это все аппарат теорфиза.
Если ты такой тупой долбаеб из шаражки - это не проблемы всего остального мира.
А аудиотренинг, про
>Тонны мукулатуры
> Что какая-то там херня
>Пиздец, вы сами от себя просто кайфуете и срете там, где люди реально занимаются наукой.
Это пиздец. Реально аудиотренинг. Пока ты себя убеждаешь, что ты не унтерменшн-неосилятор, нормальные адекватные, понимающие математику люди, продолжают ебашить спектры на кольцах и строить физическую картину мира.
А ты дальше продолжай себя убеждать, что ты не тупой, а прост все остальные фигней ненужной занимаются))
>>208825
>А почему он так необходим? Чем он крут, короче?
Если же тебя интересует сермяжный практический смысл, то из самого элементарного можно указать, например, вычисление интегралов по вычетам, или, скажем, теорию специальных функций, которая своей глубокой проработке обязана именно выходом в комплексную плоскость. Можно сказать также о квантовой физике, которая буквально пронизана комплексной переменной, начиная от самого фундамента спектральной теории и заканчивая численными методами с использованием мнимого времени. А вообще, аналитические функции обладают множеством свойств, которых нет и не может быть в вещественном случае. Взять, к примеру, теорему об аналитическом продолжении. Или строгое совпадение классов C1(D) = C∞(D). Это в первую очередь очень красивая наука, в которой практически нет места произволу, и все сущности как будто не придуманы людьми, а только ими открыты.
>>208859
Ты никогда не знаешь, что окажется востребованным завтра. Каких-то 100-150 лет назад "бесполезной" теоретической игрушкой была риманова и псевдориманова геометрия, теория групп, функциональный анализ, и многие другие вещи, без которых немыслима современная физика. Не бывает "плохой" и "хорошей" математики, это единая наука с множеством порой весьма неожиданных взаимосвязей.
Вечер в аудиторию, перельманы.
Помогите решить прикладную задачу.
У нас есть спускаемый аппарат, падающий перпендикулярно поверхности, с какой-то высоты допустим с нулевой начальной скоростью. Сопротивлением воздуха пренебрегаем сразу.
У него есть двигатели, обладающие некоторой тягой в ньютонах.
Нужно найти высоту, на которой нужно включить двигатели на полную мощность, чтобы в момент касания наша скорость тоже сравнялась с 0. Мягкая посадка короче.
Вот пик приложу, может станет понятнее. Красное - высота, зелёное - вертальная скорость.
Так вот, а теперь пойдём глубже. Двигатель во время работы потребляет топливо, следовательно масса спускаемого аппарата становится меньше. Значит тяговооруженность(отношение тяги к массе) увеличивается(то есть увеличивается ускорение, которое нам даёт двигатель).
Так вот, помогите решить эту задачу с учетом изменяющейся тяговооруженности. У нас есть начальная масса аппарата и мы знаем потребление топлива(в кг/с, например, можно использовать удельный импульс, похуй).
Как тут вообще составить мат. модель происходящего? С какой стороны подойти? Я уже весь мозг себе изъебал.
inb4: в спейсач не съебу, там нихуя не знают
>>208873
То есть вот как на этом графике - желтое ускорение. Сначала падали, потом включили двигатели, топливо вырабатывается, ускорение растёт.
Скорость падает до нуля раньше, чем на пике сверху.
Хочу запилить математическую модель, чтобы мог получить любые параметры в любой момент времени.
>>208873
>Я уже весь мозг себе изъебал.
Ну расскажи о своих попытках, что ли. Двигатель-то реактивный или любой природы?
>>208875
Реактивный же, на физику работы двигателя тоже похуй. Принимаем, что он обладает постоянной мощностью и нам известен его удельный импульс(можно выразить потребление топлива в секунду или за изменение скорости)
Сейчас уже лёг в кровать и писать о попытках с телефона неудобно. Дальше системы уравнений с постоянной тяговооркуженностью я не ушёл.
>>208873
m1*g*h2 = F_тяга_двиг*h2 + (m1 - m2)*g*h2.
h1 - расстояние от точки начала падения до точки включения двигателя.
h2 - от точки включения двигателя до точки падения.
m1 - масса до расхода топлива.
m2 - после падения.
Это если физически задачу решать. Поправь если я не прав.
>>208876
Ну смотри, у тебя в момент времени t есть аппарат массой m, считая топливо. За промежуток времени dt часть топлива dm сгорает и вылетает из сопла со скоростью U относительно аппарата. В результате скорость аппарата изменилась c V на V+dV. Пишем закон сохранения импульса
(m-dm)(V+dV)+(V+U)dm = mV
Здесь U, V, dV - векторы. Сократив всё лишнее и отбросив слагаемое -dmdV, как пренебрежимо малое, получаем очень простой закон движения.
mdV = -Udm
Разделим теперь это всё на dt
m dV/dt = - U dm/dt
dV/dt = a - ускорение аппарата.
-U dm/dt = F - сила тяги, развиваемая двигателем.
m a = F
Это и есть уравнение движения, осталось только поделить на m и дважды проинтегрировать.
>>208877
Проблема в том, что система открытая, и закон сохранения энергии не работает - по крайней мере, вот так вот в лоб. Ты не знаешь, сколько энергии унесло с собой сгоревшее топливо.
>>208877
А как выразить массу после посадки, через высоту на которой начинаем торможение? Впрочем тут вроде не сложно, завтра подумаю если ещё не ответите.
А что, если g у нас не постоянно, а зависит от квадрата высоты?
>>208878
>закон сохранения энергии не работает
Это в какой такой вселенной?
У нас есть ограничивающие условия, в рамках которых он работает.
>двигатели, обладающие некоторой тягой в ньютонах.
>Ты не знаешь, сколько энергии унесло с собой сгоревшее топливо.
Нам не нужно этого знать, это вычисляется из -
E_тяга_двиг = F_тяга_двиг*h2
А вообще есть Уравнение Мещерского для материальной точки переменной массы.
Скорее всего, если его решить твоим методом, мы получим тот же результат.
Только вот в задаче у нас не скорость посчитать, и даже не как изменится скорость под действием переменной массы.
Задача найти точку, где нужно врубить двигатель.
А это закон сохранения энергии.
>>208881
Это и есть уравнение Мещерского, я его просто вывел. Правда, для случая невесомости, но добавить силу тяготения не проблема.
>E_тяга_двиг = F_тяга_двиг*h2
Это общая работа, понимаешь? На торможение самого аппарата пошла только её часть. Остальное пошло на торможение топлива, которое впоследствии было потрачено. И ты не знаешь, какая это часть. Может быть, 10%, а может, 90%. Я тебе могу придумать придумать режим хода массы с высотой, реализующий любой наперёд заданный процент. И от этого будет зависеть ответ в задаче. А вычислить зависимость массы от высоты, учитывая, что мы знаем расход топлива - это всё равно, что решить уравнение движения. Так что никуда ты от этого не отвертишься, закон сохранения энергии тебе тут не поможет.
>>208879
m1*g*h1 = F_тяга_двиг*h2 + (m1 - m2)*g*h2.
>h1
fix
>А что, если g у нас не постоянно, а зависит от квадрата высоты?
Можно сразу брать вместо m*g закон всемирного тяготения. И интегрировать.
>>208882
>А вычислить зависимость массы от высоты, учитывая, что мы знаем расход топлива - это всё равно, что решить уравнение движения
А, понял, и правда, то есть в моем случае, придется в каждый момент времени замерять, какая часть топлива потрачена на торможение + какая часть энергии сохранилась в связи с изменением массы от расхода топлива.
>>208863
> Теория схем и квантовые группы
Я не физик, но вангую, что эта параша в жалких потугах аксиоматизировать КТП только применяется. Про суперсимметрию вообще молчу -- это не физика, а струнопердолинг.
> Алг. геом, комм. алгебра, теория схем, квантовые группы, некоммутативная геометрия, гомологическая и гомотопическая алгебра и с топологией - это все аппарат теорфиза.
Смотря что ты подразумеваешь под теорфизом. Если струнопердолинг, то возможно, но это уже не физика. Если ты про КТП или ОТО, то там эта ебола в хуй не впёрлась. Теория групп, диффуры в частных производных и тензорный анализ достаточны для конкретных результатов и расчётов, а стало быть для экспериментальных предсказаний.
> продолжают ебашить спектры на кольцах и строить физическую картину мира.
Ох лол, кто там строит? Полтора клоуна, которые под Виттена пытаются косить? Те, кто в физике делает какой-то профит, давно ушли в эксперименты и ебашут по хардкору в ЦЕРНах и Макс-Планках. Твоя теория струн нинужна, смирись и ебашь дальше, матешу школьникам преподавать, крикливый бля.
>>208870
> и все сущности как будто не придуманы людьми, а только ими открыты.
Ну да, я уже давно хотел сказать, это наш корявый порванный платонист стиль сменил.
>>208922
Мм ясн))
>>208922
> Я не физик
Дальше не читал
Космонавт - долбоёб опять выходит на связь.
Принёс три графика, точно иллюстрирующих мою задачку.
Сейчас буду ебаться, пытаясь выразить высоту, на которой начинаем торможение.
Математик-бакалавр врывается в тред. Спрашивайте свои ответы
матан, всевозможные дифуры, функан, числаки
>>208877
>(m1 - m2)*g*h2
Это типа решение интеграла от m1 до m2 (mgh)dm ?
Тут же по идее нужно пилить двойной интеграл, h же тоже изменяется.
>>208878
Скорость истечения газов нам не дана(можем посчитать ну да похуй). Лучше считать, что у нас магический двигатель, обеспечивающий нас подъемной силой F и аннигилирующий m* кг/с топлива во время своей работы.
И всё равно я нихуя не понял.
>>208993
Тот же график, построенный относительно высоты, а не времени.
Относительно высоты напрямую вообще нихуя не зависит. Я решительно нихуя не понимаю.
>>208995
Сколько существует абелевых групп порядка 14674545 с точностью до изоморфизма?
>>208922
>Я не физик
>параша
>жалких потугах
>пердолинг
>уже не физика
>в хуй не впёрлась
>Полтора клоуна
>теория струн нинужна
>матешу школьникам преподавать
>корявый порванный платонист
Всё ясно. Зря я потратил на тебя время.
>>208998
>Скорость истечения газов нам не дана
Она была нужна только для вывода. Для вычислений ты смело можешь считать, что тебе дана сразу
>-U dm/dt = F
А дальше всё очень просто же. У тебя есть величина F (которая складывается из тяги двигателя и гравитации), есть зависимость m(t).
x'' = a = F/m(t)
И интегрируй это, не забыв про начальные условия. Получишь зависимость высоты и скорости от времени после включения двигателя (t = 0). Дальше простая арифметика.
Давай статью с конкретным примером расчёта с применением схем и квантовых групп. Чтобы был расчёт сечения, например.
Давай. Ждём.
>>209014
> примером расчёта
Очередное быдло, которое неосилило ни абстракцию, ни физику, кукарекает о вычислениях)))
>>209056
Статью давай. Я осилил эти области получше тебя, поэтому и спрашиваю.
сап, математики.
Можете пояснить, чем в данный момент занимается теория множеств?
Какие результаты сейчас достигаются ?
Все таки 21 век на дворе. Зачем люди занимаются этим сейчас.
>>209078
Ну как чем? Ёблей в жопу, конечно. Одного из таких ебунов можешь наблюдать выше по треду.
с вами снова математик-бакалавр. буду постить рандомную геометрию.
>>209004
расскажешь, зачем тебе -- может, посчитаю.
>>209078
если коротко -- >>209080 прав. Если бы всё было у них гладко и успешно, уже объявили бы существование единой модели, не вызывающей противоречий. Лучше всего -- зайди на архив.орг, дельные статьи там иногда появляются.
Я жду от тебя статью, платончик, про применение схем в КТП (не теории струн) вне её аксиоматизации. Или ты в пузырёк залез?
>>209080
Примерно так себе я это представлял.
У нас на кафедре есть просто несколько людей, которые с чем-то там ебутся, потом чето там докладывают.
Мне все время воспитание мешает спросить, что за хуйню я только что слушал.
>>209078
Построением разнообразных моделей теории множеств, удовлетворяющим разнообразным экзотическим свойствам. Характерный вид доказываемых теорем примерно таков:
Пусть существует большой кардинал A. Тогда существует модель теории множеств B, в которой выполнена теоретико-множественное свойство C, верна гипотеза D и существует большой кардинал E.
Здесь, скорее всего, A, C и E были предложены в 30-е - 60-е, B - это вариация на тему ZFC, D - это либо гипотеза из ранней теории множеств, либо из какой-то теоретико-множественной области математики (общая топология, абстрактная алгебра, теория моделей и т.п.). Некоторые части этой формулировки могут опускаться.
Или иными словами, это весьма техничиская область в которой занимаются более-менее одним, весьма своеобразным, типом задач и >>209080 - прав.
>>209154
Этот вычислитель порвался, несите следующего))
Можт ты еще спизданешь, что категории не нужны, кроме теории струн? Пиздос, категории даже в квантмехе применяют. Твоя проблема в том, что ты тупой утенок, студент какого-нибудь задрищенского физфака, который не хочет смотреть правде в глаза, что твоего умишка никогда не хватит не то что на создание теории, да ебать, тебе не хватает умишка на осиливание теории. Продолжай устраивать аудитренинг себе дальше)) Всем тут все с тобой ясно))
>>209139
> расскажешь, зачем тебе -- может, посчитаю.
На такие вопросы сходу отвечают вообще-т. Подсчет конечных абелевых групп - легко разрешенная проблема, а теорему о строении абелевых групп конечнопорожденных(как частный случай теоремы о строении конечнопорожденных модулей над кольцами главных идеалов) знает любой первокурсник мухосранска.
>>209236
>категории даже в квантмехе применяют
Конечно же не применяют - и ты это знаешь. Поэтому тебе так и разорвало
>))
>аудитренинг
>>209236
и что? ты меня этим опустить хочешь? мне на высшую алгебру вообще насрать. есть разные области математики, и разным людям нравятся разные области. тебе -- алгебра, алгебраическая геометрия,наверное, если Миши Вербицкого перечитался. я это выучил и с радостью забыл. если будет стоять вопрос жизни и смерти -- вернусь, а сейчас оно мне не всралось. я ж не спрашиваю о методах построения функции Грина произвольной области и тому подобного.
>>209237
Так значит я в точку попал с студентом задрищенского физфака)) Проецируй дальше))
Теперь я буду звать тебя утенок, ты ведь не против?
>>209251
>КУДАХ БАБАХ КУКАРЕКУ))
>отсутствие примеров и ссылок на применение категорий в квантмехе
Вот и пруфы. Таким образом фиксирую: категории в квантовой механике не применяются.
Кстати, хацкель тоже кривое говно для быдлокодеров - но ты других языков не знаешь да и хацкель не знаешь, петушок из /зк.
Так-то.
>>209254
Пздц, такой тупой утенок, который не перестает проецировать)
http://arxiv.org/pdf/0808.1023v1.pdf
Первая ссылка в гугле)
>петушок из /зк.
Эт ты себя классно назвал) Возьму на заметку, петушок-утенок)
Алсо, судя по тому, что на слово "теоркат" ты отозвался "хаскелл", следует, что теорката ты не знаешь, мой дорогой петушок)
Если для тебя теорфиз, а алг. геом(со всеми схамами) и теоркат, да и гомологическая с гомотопической алгеброй - его язык, не физика, ну что я могу сказать, не мои проблемы, что в твоей шаражке на физфаке это не изучают))
>>209257
>http://arxiv.org/pdf/0808.1023v1.pdf
Ну вот так бы сразу, а то раскукарекался как школьник на перемене.
>схамами
Спокойней, няша, не нервничай. И не оправдывайся.
>>209259
http://www.numdam.org/item?id=PMIHES_1988__68__175_0
гугл по algebraic geometry in quantum field theory
Выдал мне: http://www.numdam.org/item?id=PMIHES_1988__68__175_0
Так что оправдывай свое ничтожное существование дальше, петушок-утенок)
Поясните за гипердействительные числа, посоны.
>>209260
>http://www.numdam.org/item?id=PMIHES_1988__68__175_0
>Выдал мне: http://www.numdam.org/item?id=PMIHES_1988__68__175_0
Так что тебе, говоришь, гугл выдал?
не дергайся ты так, анимешка, нервы береги
>>209263
Тебе Зоуичка что-ли не нравится? Или ты просто в гипердействительных числах не шаришь?
>>209265
Ну скажите ему, посоны!
>>209270
Хотел бы оказаться на месте этого парня? я - да. Несколько секунд тинейджер ловила максимальный кайф, это там где она голову запрокинула
http://www.xvideos.com/video6576145/teenagers_first_selfshot_sex_homevideo
>>209236
> кукареку категории кукареку
Так и будешь вилять хвостом, болван?
Математику и категории в частности я знаю лучше тебя -- это даже не вопрос дискуссии.
Вопрос к тебе конкретный: ты залупнулся о незаменимости схем в КТП -- докажи это ссылкой на статью. Следующие топики исключены: аксиоматизация КТП и теория струн.
Ты сколько раз ещё позориться будешь?
>>209257
> Первая ссылка в гугле)
Во дурак. Сразу демонстрирует твоё полное непонимание предмета.
> http://arxiv.org/pdf/0808.1023v1.pdf
Категории, конечно сексуальны, но эта статья имеет нулевую ценность для физики и даже, для математики. С переписываниями знакомых и хорошо работающих матаппаратов в категорный вид я знаком. Есть даже попытка в применении ТАУ. Но это всё баловство и желание выбить публикацию. Никаких мат. открытий в таких статьях не делается, никаких важных теорем не доказывается. А для физика это всё ненужные финты ушами. Разумеется, расчётов такие подходы тоже не облегчают. Амплитухедрон и то более обнадёжевающ.
И, кстати, самое начало статьи тебе и говорит о том, что речёт идёт о foundations, то есть аксиоматике.
>>209260
Опять гугл. Так ты вообще не сечёшь в том, что порешь, раз тебе в гугл лезть надо. Вот же глупышка. И приплёл, главное, поехавшего Атию, я так и знал. И опять аксиоматизация.
Дурак, ты пойми, физикам до ебени твои жалкие потуги аксиоматиизировать КТП -- им на это НАСРАТЬ. НАСРАТЬ, понимаешь, дебли бля? Нравится тебе это или нет, можешь сколько угодно смайло- и аватаркофажить, только бани добьёшься.
Вы занимаетесь хуйнёй какой-то, пацаны. Какая разница что где применяется?
>>209340
Мудак.
>>209334
Пиздос, второкур-физфаковец, тебе еще не надоели эти твои жалкие оправдания?
Покажи мне пример, где применяется интеграл по траекториям, аксиоматизация КМ и прочей хуиту - исключается.
Пиздос, ты вообще что такое теорфиз знаешь, утенок?
Пруфы дал - дал. Если для тебя теорфиз - это не физики, но проблемы утят меня не волнуют.
Хотя, ты зелень обычная скорее.
>>205975
> Теорема Безу является очевидной по модулю теории когомологий.
> Теорема Безу утверждает, что остаток от деления многочлена P(x) на многочлен (x-a) равен P(a).
ЛОЛШТО? Ну охуеть теперь, без когомологий тут никак не разобраться.
>>205982
Если получены новые значительные результаты, то так уже нельзя сказать
>>209345
Ну а если эти результаты можно получить используя несколько формализмов? То какой формализм петушиный, а какой тебе нравится?
>>209340
Никакой. Любое направление в науке ценно само по себе, независимо от того, сводится оно к пивасу и семкам или нет. Печально, что кто-то в этом разделе этого не понимает.
>>209355
первый формализм получивший новый результат - годный формализм.
Формализм который способен только на кококо и перемалывание всем давно известного - петушиный
Парни, поясните на пальцах за отношения эквивалентности и, в частности, за классы эквивалентности. Читал книгу Роберта Столла о множествах, читал "Алгебру" Ван дер Вардена, но нихуя не понял.
В частности мне не понятно, почему не пересекаются классы эквивалентности? Допустим, есть класс эквивалентности сравнения по модулю 2, есть класс эквивалентности сравнения по модулю 4. Они вполне могут содержать одни и те же элементы/пары, но в конце-то концов множества этих элементов не совпадают (или совпадают?).
>>209388
Ты рассмотрел классы двух разных отношений эквивалентности.
>>209388
Нет не так. Мы фиксируем одно и только одно отношение эквивалентности.
Тогда, наше множество разбивается на не пересекающиеся классы. Тогда фактормножество - это множетво этих классов.
Как в твоем примере: отношение под модулю два, тогда целые числа рспадаются на четные и нечетные.
>>209343
Не виляй хвостом, клоун. Ты выглядишь идиотом. Ответ на твои "пруфы" -- >>209335
Ты вообще понимаешь разницу между интегралом по траекториям и аксиоматизацей, плебей? Ты понимаешь, что первое (включая диаграммы, S-матрицы, ряды Дайсона) -- это аппарат расчёта? Разницу между КМ и КТП вообще улавливаешь?
А про ренормализацию слышал? Так вот почитай получше и ты поймёшь, что потуги некоторых Атий (который ярый платонист) появились не на пустом месте. А физикам математическая чистота до задницы, видишь ли. От одной только дельта-функции в своё время пердаки бомбили у некоторых особо упоротых математиков.
Короче ты снова выставил себя некомпетентным кривляющимся дураком.
Подходящего треда не нашел, спрошу здесь. Существуют ли какие-то геометрические законы (параметры, соотношения?), описывающие тело человека? Кто-нибудь данимался этим вопросом вообще? Интересует любая информация по этой теме.
>>209431
Я понял, что ты игнорируешь факты и пускаешь всем пыль в глаза, вместо адекватной аргументации.
Поссал в рот второкуруфизфаковцу. А теперь уебывай отсюда, петушок.
Ты ведь даже понять не можешь, что категории - это язык, а не другой способ теории строить.
Вон, гомологическую топологию вовсю ебашат в теорфизе, но гом. топ. без категорий изучать - только конченный дебил будет. Ибо функориальные свойства позволяют сходу заебашить спектралку.
Но куда тебе до этого, ты ведь просто зеленый.
>Ты вообще понимаешь разницу между интегралом по траекториям и аксиоматизацей, плебей?
> Ты понимаешь, что первое
> это аппарат расчёта
H@H@H@H@H@H@H@H@H@H, OH WOW SHI~
Ну ты точно просто толстишь в этом итт треде.
Не буду больше тебя кормить, няша :3
>>209438
Не переводчик выставил тебя идиотом. Ты сам себя им выставил.
Я чувствую, что нас великое гиперкомплексное будущее! Математики покорят новые вершины абстракций, сплочённые единой идеей познания мира. Все мы браться по разуму)
>>209435
>параметры, соотношения?
Занимался Леонардо Да Винчи
Поясните за комплексные числа. В чем их суть? Какую роль они вообще играют в математике? Помню, что когда выводили уравнение колебаний, то там искали решение в виде чего то там с мнимой частью. В чем физический смысл получается?
>>209621
d gbplt ndftq vfvrb gtne[
cosx + i sinx = eix => cosx = Re eix, sinx = Im eix
Заскулил как щенок, как его на место поставили.
>>203761
Аноны, а объяснить, на механике дают зубрить вычислительные рецепты или дают с доказателсьтвами и самому надо доказывать те разделы математики, что они изучают?
>>209851
Ах, да, и можно ли после механики поступить в магистратуру/аспирантуру на математику?
Анон, я хочу начать изучать математику именно как науку, но не знаю, с чего толком начать. Школу прогуливал, но что-то по бокам ухватывал.
Почему для функции Грина справедлив пикрелейтед? Если явно посчитать, например, для оператора d²/dx²+1 , то хуйня выходит. А если использовать непрерывность (и следовательно ограниченность), то интеграл будет меньше площади прямоугольника, который в пределе "сожмётся".
>>209893
>но не знаю, с чего толком начать
Выеби свою мамку, очевидно же. Все великие математики так начинали.
>>209901
Можно подробней? Как именно?
А в школе не заставляют ебать мамок, потому что упрощённый курс?
Как так получилось?
Аноны, мне 17 лет. Хочу приобщиться к математике. В школе не учил совсем, думал не дано, физику и химию знал. Перед экзаменами подготовился и за месяц немного выучил, что позволило сдать успешно экзамены, и поступить в универ. Я был самым хуевым математиком в классе, через свою лень, а сдал лучше всех, и поступил в универ. Там где буду учиться, математика будет только первые два года, мне на это пофиг.
Как стать математиком по вашему определению? Как вылезти из недошкольного уровня, и выучить науку, которая заставляет бугуртить.
Блядь, это что, вайп школьниками?
>>209912
Самоучкой почти без шансов. Нужен оче хороший универ. Говорят в рашке таких нет. Сожылею. Но можно и в плохом поучится. Попробуй напиши какому-нибудь знаменитому математику, например Роману Михайлову или Terence Tao или Вербицкому (или всем сразу) и спроси что делать.
Это могут быть вредные советы, я всего-лишь мимоинжынер.
>>209914
так каникулы жы дети набигают в интеренты. Дяденька олдфаг наоборот должен радоваться, что детишки полезли в науку, а не на аниму дрочат и в игоры гоняют. Я жы с нормальными соображениями. Ну все, захламлять вам тут не буду, слава Арстроцке математике
Как же вы, однако, заебали. Давайте пруфы того, что "самоучкой почти без щансов". Готов поспорить, что все неплохие физики самостоятельно учат нужную математику, а не по ВУЗу.
>>210596
Ты сидишь за компом, который придумали инженеры-физики. Ссу тебе в рот.
>>210593
Выучиться самому разумеется можно.
Однако нужен хороший самоконтроль и большое желание понять все в деталях.
Поясню в чем дело:
1. В универе тебя контролируют контрольными, сессиями, коллоквиуами и прочим.
2. Когда ты чего не понимаешь ты легко можешь спросить у преподователя или других студентов.
Одному тебе придется все непонятные места разбирать самому. Тут здесь есть один простой совет: если тебе непонятен какой-то кусок доказательства или суждений, ты обязательно должен вернутся назад и прочитать снова часть, которая тебе сейчас непонятно. Ну или хотя бы прогуглить этот момент.
>>210597
Ахуительные сказки. Физики у него компьютер придумали. Бабка старая всех компьютерщиков программистами называет, а ты всех подряд в физики гребёшь. Дебил натуральный.
>>210599
1. насильно мил не будешь, бро. алсо самостоятельность мышления убивается тупой зубрёжкой по чужим программам.
2. было актуально лет десять назад. сегодня же интернет отвечает на вопросы лучше, чем какой-то рандомный препод.
Другое дело, что вузик - это по идее-то доступ к дорогостоящей технике (которого я в своей мухосрани не имел - лишь сейчас, знакомясь со специалистами и заинтересовывая их своими идеями я обретаю возможности, которыми должен был обладать по дефолту)
>>210608
НУ ЕСЛИ ТЫ ОЧЕВИДНОЕ НЕ ПОНИМАЕШЬ...
НУ ДАВАЙ матиматик СДЕЛАЙ МНЕ КОМПЬЮТЕР!
болтун несоображающий
>>210602
1. Стимулирует дисциплину же все равно.
1.1. Зубрежка это вообще не обучение. У нас преподы всегда спрашивали на понимание, идею.
2. Где ты находишь такие ресурсы, где объясняют, лучше чем ИРЛ объясняют кандидаты и доктора наук?
>>210602>>210593
Поясняю за математику, но подозреваю, что во всех науках так. Всё полная хуйня по сравнению с людьми и ебаным коллективом. Важнее всего общаться, общаться и общаться. Посещать разные семинары, ездить в разные школы, даже пить водку после занятий. Конечно, надо и книжки читать, но без общения очень все печально с какого-то момента. В конце концов надо еще понять, что читать, а также получить должную мотивацию. Ну, т.е. сложно читать что-то сложное, если изначально не понять из пиздежа, зачем это все вообще надо, и не привыкнуть ко всяким умным словам. Ну, и
>было актуально лет десять назад. сегодня же интернет отвечает на вопросы лучше, чем какой-то рандомный препод.
Совершенно не верно. Ну, т.е. категорически не верно. Если ты хочешь узнать просто факт, то да. Но если, например, не понимаешь определения или доказательства какого-то, то гугл очень вряд ли поможет.
Предсказуемо, образованцы никаких серьезных аргументов или фактов не привели. Вы не подумайте, я ценю (более-менее) ваши мнения, как формально более образованных людей, но логика ваша отдает запашком несвежей рыбы и привкусом балтики семь.
Действительно,
>>210599
> Однако нужен хороший самоконтроль и большое желание понять все в деталях.
Если нету самоконтроля, ты ничего не добьешься в любом случае, какой бы ошейник (в данном случае ВУЗовский) ты на себе не примерил. А если бы не было желания, я бы подобные вопросы и не спрашивал, и не интересовался бы математикой, а сдавал бы её зубрежкой, чтобы побыстрее освободить время для других дел.
> Поясню в чем дело:
> 1. В универе тебя контролируют контрольными, сессиями, коллоквиуами и прочим.
Так знатно контролируют, что испокон веков любой мыслимый тест сдается на отлично зубрежкой. О своей памяти я прекрасно позабочусь сам. В любом случае лучше, чем одна-две проверки с полугодичным разрывом.
Иначе как же так выходит, что 100% окончивших ВУЗ помнят в лучшем случае 1% от того, что изучали?
> 2. Когда ты чего не понимаешь ты легко можешь спросить у преподователя или других студентов.
А могу использовать собственный мозг и альтернативные учебники. Кстати, такой подход за несколько лет обучения сильно прокачает мозг. А то, что ты предлагаешь, только приучит ложиться на других и быть неуверенным в своих силах.
Кроме того, не забывай, что речь идет о самостоятельном обучении во время обучения в ВУЗе - потому что бумажка-то нужна, а тратить несколько лет перед вузом на изучение всей математики - непозволительная роскошь. Хотя, я уверен, что годик всё же потратить следует. Именно так сам и поступаю. Через год отпишуся.
> Одному тебе придется все непонятные места разбирать самому. Тут здесь есть один простой совет: если тебе непонятен какой-то кусок доказательства или суждений, ты обязательно должен вернутся назад и прочитать снова часть, которая тебе сейчас непонятно. Ну или хотя бы прогуглить этот момент.
Напомню, что во время исследовательской деятельности, никто тебе непонятные места помогать разбирать не будет - отчасти потому что они еще пока всем непонятны. Ты так говоришь это, как будто это что-то плохое.
>>210612
> Всё полная хуйня по сравнению с людьми и ебаным коллективом. Важнее всего общаться, общаться и общаться. Посещать разные семинары, ездить в разные школы, даже пить водку после занятий. Конечно, надо и книжки читать, но без общения очень все печально с какого-то момента. В конце концов надо еще понять, что читать, а также получить должную мотивацию. Ну, т.е. сложно читать что-то сложное, если изначально не понять из пиздежа, зачем это все вообще надо, и не привыкнуть ко всяким умным словам.
Семинары - это хорошо, но пруфов твоему кукареканью социобляди я не вижу. Понимаешь, если бы у тебя был хоть какой-то авторитет, как например трип успешного тракториста, делающего свою тему, твои слова еще могли бы чего-то стоить. А так получается, что ты - скорее всего бессознательно - позиционируешь свой аргумент как аргумент от авторитета, но таковым не являешься.
Твои предложения кричат о тебе, как о человеке, слабом волей и, возможно, умом.
Резюмируя, я в очередной раз в дискуссии на эту тему от противоположной стороны вижу в сущности лишь "это хорошо и удобно, если ты безвольный распиздяй с посредственным умишком". Вот только посредственные умишки никогда к углубленным знаниям и их полному пониманию не стремятся - они нехотя жрут, что им дают.
Долбаеб ИТТ, поясните за аксиому выбора, мне кажется полной хуйней, как можно не боятся доказывать с помощью ее, что-то?
>>210685
>есть академ. справка о завершении двух курсов в тех. ВУЗ'е.
>16
>>210687
Ну берёш карочи и такой не баишься карочи. А теперь проваливай. Следующий!
>>210687
Это самая винрарная аксиома эвер. Столько-то пердаков интуиционистоблядков подорвала.
>>210707
Сука, я так понял там множество из чего угодно, блять, это тоже самое, что сказать, мол бог есть патамушта есть!
>>210710
То есть она абсолютна верна и никакого кризиса математики не вызовет в чьем-то анусе?
>>210677
>Семинары - это хорошо, но пруфов твоему кукареканью социобляди я не вижу. Понимаешь, если бы у тебя был хоть какой-то авторитет, как например трип успешного тракториста, делающего свою тему, твои слова еще могли бы чего-то стоить.
Я, конечно, пока не математик, но математикой уже сколько-то прозанимался и именно к занятиям наукой иду. Более или менее вижу, как все устроено. А вот ты явно говоришь кукарекаешь с дивана. А то, что я сказал вполне общепринято, всякие Миши и Тао подтвердят.
>Так знатно контролируют, что испокон веков любой мыслимый тест сдается на отлично зубрежкой.
Ни в одном приличном месте тестов нет. Хотя контроль знаний действительно для слабаков. Но именно контроль ради контроля. А вообще листки и экзамены нужно сдавать, суть не в том, чтобы тебя подстегивать, а чтобы осознавать, что ты понимаешь, а что и нет.
>А могу использовать собственный мозг и альтернативные учебники.
Ну, удачи. Будешь сильно тормозить, а во многих случаях так принципиально не помочь. Ответь с помощью альтернативного учебника на вопросы типа "Нахуй вот это вообще надо", "А что если в теореме ослабить вон то условие", "Почему нельзя просто..."
>Кстати, такой подход за несколько лет обучения сильно прокачает мозг. А то, что ты предлагаешь, только приучит ложиться на других и быть неуверенным в своих силах.
Какой-то ебанутая у тебя позиция. Не стоит воспринимать науку как спорт. Наука дело сугубо коллективное и совершенно независя в прокачке мозгов. Ты хочешь "качать мозги" (по-моему совершенно мифическая деятельность) или математику учить?
>Напомню, что во время исследовательской деятельности, никто тебе непонятные места помогать разбирать не будет - отчасти потому что они еще пока всем непонятны
Вот опять таки совершенно неправильный взгляд. В исследовательской деятельности нужно максимально общаться с людьми и разбираться вместе, обмениваться идеями. Стереотип об ученом одиночке, который сидит в подвале и что-то дрочит, давно устарел.
>>210687
А чем она тебе не нравится?
>>210734
>А чем она тебе не нравится?
Это здешний конструктивистоблядок пытается развести срач. Не обращай внимания, что взять с поехавшего.
>>210770
Ну, просто обычно люди недовольны, например, каким-нибудь парадоксом Банаха-Тарского. Но, блджадь, это же совершенно очевидно, что объема не существует, множества слишком хуево бывают устроены.
>>210712
Ну типа того.
>>210710
Ну тут мотивация глубже, чем просто избавиться от аксиомы выбора, тащемта.
>>210714
Как понять "верна", дурак? Классическая теория множеств вместе с аксиомой выбора может быть в лучше случае непротиворечива (не вести к парадоксам), но это нельзя доказать, используя только аксиомы теории множеств. Алсо аксиома выбора независима от остальных. То есть нельзя вывести эту аксиому из остальных.
>>210770
Отнюдь, я давно не создавал тредов (кроме этого), потому что пока нет достаточно интересных тем для меня вне работы. И, кстати, "блядок" и "поехавший" ты сам, уёба :)
>>210785
Очевидно, говоришь? Ну-ну. Давай, рассказывай, что там "очевидного" в данной теореме. Начни с того, насколько и почему для тебя "очевидна" аксиома выбора. Ну так чисто интуиитвно. Подумай на досуге.
>>210816
Имелось ввиду, что я не развожу срачи. Про аксиому выбора спросил какой-то дурак.
>>203761
Анон, хочу изучить математику. О ней знаю на уровне 6-классного школьника. Какие книги посоветуйте? Может, есть адвайслист?
>>210816
>насколько и почему для тебя "очевидна" аксиома выбора.
Очевидна необходимость аксиомы выбора.
Пусть S - расчленённое семейство произвольных непустых множеств. Возникает естественная потребность получать подмножества из объединения множеств семейства (т.е. подмножества из ∪S). Оказывается, что подмножества определенных типов - представляющих собой элементы прямого произведения ∏S - невозможно получить только с помощью аксиом ZF. Следовательно, чтобы иметь возможность работать со всеми типами множеств, необходимо постулировать свойство, которое позволяет таким множествам существовать. То бишь, принять как данность то, что прямое произведение множеств семейства ∏S непусто.
В общем-то, необходимость аксиомы выбора так же логически неизбежна, как и необходимость существования аксиом ZF, поэтому аксиома выбора не менее очевидна, чем другие аксиомы. К тому же, с силу независимости, без аксиомы выбора мы потеряем достаточно весомую часть математики.
другой-кун
>>210734
> А вот ты явно говоришь кукарекаешь с дивана.
Чтобы оперировать логикой внедиванное пространство не нужно.
> Ни в одном приличном месте тестов нет.
Я назвал тестом любую проверку, потому что так переводится это слово.
> а чтобы осознавать, что ты понимаешь, а что и нет
Ни один тест это не проверит. А осознавать, что я понимаю, я могу и без посторонней помощи. Потому что если, понимаешь, я чего-то не понимаю - то я, так бы-то сказать, понимаю это.
> Будешь сильно тормозить
Да хуйня. И куда спешить, в любом случае?
И снова таки я узнаю эти расплывчатые смазанные аргументы распиздяефажиков. Оно-то понятно, всем практически лень присуща, но зачем свою лень прикрывать диалектикой?
> а во многих случаях так принципиально не помочь
Хорошо, это можно допустить. Но что мешает время от времени быть свободным слушателем на лекциях и там же спрашивать ведущих о набежавшем?
> Ответь с помощью альтернативного учебника на вопросы типа "Нахуй вот это вообще надо", "А что если в теореме ослабить вон то условие", "Почему нельзя просто..."
Мне совершенно нетрудно представить такую ситуацию. Описания везде разные, когда один недоговорит о чем-то, другой с радостью всё прояснит для даунов. И самостоятельное отвечание на такие вопросы как раз и есть деланье математики. А не "принятие" приведенных доказательств с последующей дрочкой упражнений. Не в той мере, то есть.
> Ты хочешь "качать мозги" (по-моему совершенно мифическая деятельность) или математику учить?
Качание поможет её учить. Совершенно не мифическая, читни статей про исследование мозгов математиков.
> В исследовательской деятельности нужно максимально общаться с людьми и разбираться вместе, обмениваться идеями
То есть снова идет надежда на других. Я, вообще говоря, понимаю это, но тут нужно держать в уме правило 90%. Я к тому веду, что нужно самому не плошать.
>>209896
Здесь теорема о среднем должна сработать. А с оператором проверь себя: правильно функцию Грина нашёл?
>>210832
>Ни один тест это не проверит. А осознавать, что я понимаю, я могу и без посторонней помощи. Потому что если, понимаешь, я чего-то не понимаю - то я, так бы-то сказать, понимаю это.
Ну нет же. Вот в России стандартный способ обучения математике это система листочков. Людям дают листки с задачами, которые они должны решать и устно рассказывать. Спрашивать могут что угодно по теме и заодно залатывать дыры в образовании. Во время такого разговора зачастую гораздо глубже начинаешь понимать проделанное и осознавать, что не сделал. Даже банальный экзамен с нетривиальными задачам показывает, что понимаешь, а с чем проблемы. И
>Потому что если, понимаешь, я чего-то не понимаю - то я, так бы-то сказать, понимаю это.
Совсем неверно. Лажануть и не заметить можно миллионом способов. Откуда по-твоему в научных работах ошибки или они все дураки, а ты не такой. Порой очевидным кажется неверное, а порой кажущееся сложным на самом деле дурацкая тавтология (например, матан и линейная алгебра по большей части набор очевидных утверждений). Тут нужно какое-то чутье, которое со временем появляется (хороший пример топология с доказательствами на пальцах, где надо понимать, что можно так делать, а что нельзя).
>И куда спешить, в любом случае?
>Но что мешает время от времени быть свободным слушателем на лекциях и там же спрашивать ведущих о набежавшем?
Откуда я знаю, что тебе надо. Я просто утверждаю, что без людей тяжело.
>Мне совершенно нетрудно представить такую ситуацию. Описания везде разные, когда один недоговорит о чем-то, другой с радостью всё прояснит для даунов.
У всех людей свои баги, а подобные вопросы выходят за рамки любого учебника.
>И самостоятельное отвечание на такие вопросы как раз и есть деланье математики.
На некоторые вопросы сам не ответишь, так как банально не знаешь многого. Например, на резонный вопрос первокурсника "А нахуй эти абстрактные кольца вообще нужны?" придется привлечь достаточно знаний из тч и алгебраической геометрии как минимум. Опять-таки у каждого свои особенности, большинству ответ на такой вопрос не особо то и нужен (зато нужен на другой подобный).
>Совершенно не мифическая, читни статей про исследование мозгов математиков.
С удовольствием читну (даже без сарказма), только ссылки кинь. А то я пока никакой связи не замечал кроме, разве что, следствий некоторого отбора (не всякий может и хочет заниматься математикой).
>>210816
>Очевидно, говоришь? Ну-ну. Давай, рассказывай, что там "очевидного" в данной теореме.
Я не говорил про теорему. Просто утверждение, что каждому подмножеству R^n можно разумным образом сопоставить объем кажется очевидно неверным чисто интуитивно. Если эти ощущения формализовать, то получится доказательство парадокса Банаха-Тарского. Поэтому для меня этот аргумент относительно плохости аксиомы выбора никогда не работал. Я к тому, что так и не понял, чем она тебе не нравится? Чем хуже какой-нибудь аксиомы выделения?
Не уверен что я там где нужно, но это самый близкий по тематике тред.
Вопрос касается криптографии. Один знакомый мелет мол "Aes говно, я выбираю BitRotate". BitRotate это сдвиг по байтам, то бишь шифр цезаря, но в байтах. Шифр цезаря можно запросто взломать частотным анализом, но там буквы, а прокатит ли такое с байтами?
1)в байтах "алфавит" состоит из 256 "символов"
2)Если в тексте на человеческих языках есть определенные слова с определенными буквами, то HEX, то бишь байтовый "текст" это просто каша и поток говна
>>210836
Решал задачу пирелейтед. Посмотри сам, там не получается ноль никак, если проинтегрировать уравнение.
Краевые условия были в нуле и pi/2 - нуль.
>>210838
> Спрашивать могут что угодно по теме и заодно залатывать дыры в образовании.
Проблема тут в том, что подавляющее большинство - даунята, неспособные в понимание принципиально. Если действительно задавать им вопросы на понимание, то получиться, что большую часть студентоты придется кикнуть, а остальная будет троечниками. По этой причине вопросов на мышление практически нет.
> Откуда по-твоему в научных работах ошибки
Если ты имеешь в виду ошибки невнимательности, то причем здесь ошибки из-за недостатка понимания?
> Откуда я знаю, что тебе надо.
Я же сказал: изучить предмет с полноценным пониманием и без никаких урезаний, что обучаясь в ВУЗе сделать невозможно. Обучаясь самостоятельно, обучаясь в ВУЗе, с другой стороны видится мне решением.
> Я просто утверждаю, что без людей тяжело.
Бессмысленное утверждение. А еще математику изучать тяжело. Дальше что?
> На некоторые вопросы сам не ответишь, так как банально не знаешь многого
А зачем ответы на вопросы, ответы на которые получишь гораздо позже в процессе обучения? Таки нашел себе ответ - сам или через вики, или более адвансед учебник - хорошо, не нашел - просто продолжаешь, пока не дойдешь до места, где станет ясно.
> только ссылки кинь
В гугле забанили? Гугл сколар, на тему пластичности мозга. С точки зрения эволюции это очевидно, значение имеют лишь масштабы явления. А их как раз уже частично изучили.
>>210831
> Очевидна необходимость аксиомы выбора.
Необходиомсть? Тогда я мог неправильно понять утверждение. Потому что, например, для меня сама аксиома неочевидна. Сомневаюсь, что у кого-то по-другому.
> логически неизбежна
Это ещё что за зверь "логическая неизбежность"?
> необходимость существования аксиом ZF
Почему именно ZF? А почему не интуиционистской теории типов, а почему не аксиом теорката? А почему не аксиом структурной теории множеств?
> без аксиомы выбора мы потеряем достаточно весомую часть математики
Да, весьма весомую. Но, смотря для кого.
>>210839
> каждому подмножеству R^n можно разумным образом сопоставить объем кажется очевидно неверным чисто интуитивно.
Ну, во-первых, "очевидность" теоремы Тарского зависит от "очевидности" аксиомы выбора как и само существование неизмеримых множеств.
> Я к тому, что так и не понял, чем она тебе не нравится? Чем хуже какой-нибудь аксиомы выделения?
Как понять "не нравится"? Где я такое сказал? И, кстати, если пользоваться такой классификацией "плохости", то все импредикативные аксиомы "плохи".
>>210859
>Потому что, например, для меня сама аксиома неочевидна. Сомневаюсь, что у кого-то по-другому.
Лол. Ты ещё сомневаешься? Весёлый у тебя манямирок.
>Это ещё что за зверь "логическая неизбежность"?
А что непонятого-то? Логически неизбежна в рамках подхода принятого Цермело и Френкелем. Только не стоит воспринимать это выражение как строгое математическое понятие, это скорее расхожая фраза.
>Почему именно ZF?
А почему бы нет? Как пример. Имелась в виду необходимость полного набора аксиом ZFC для аксиоматизации классической теории множеств. Выкинув любую из них, мы либо придем к противоречию, либо потеряем возможность рассматривать важный для математики, в целом, класс множеств, полученный посредством этой аксиомы. Так вот, в этом плане аксиома выбора так же необходима, как и остальные.
>Да, весьма весомую. Но, смотря для кого.
Для всех, кто не входит в твой манямирок. Мы потеряем часть классической математики.
>>210855
Смотри, функция 2 переменных, по прямой x=s разрыв. (интегрирование ж не в обобщённых функциях, вроде) Тогда разбиваем на 2 участка, от s-e до s и s до s+e. На каждом из них она непрерывная, какая хочешь гладкая итд. Применяем теорему о среднем. Значение в хер знает какой точке на бесконечно малую (таких 2 слагаемых). Это хер знает какое значение ограничено. Переходим к пределу. ЧЯДНТ?
>>210875
> манямирок
> манямирок
Туда ли ты зашёл, чучело?
>
> Логически неизбежна в рамках подхода принятого Цермело и Френкелем.
Ну ты и словоблуд. "Логически неизбежна" и "логически неизбежна для такой-то аксиоматики" -- это одно и то же? Логика хромает, парниш.
> А почему бы нет?
А почему бы нет, правда? А почему не ITT, HoTT, структурная теория множеств, альтернативная теория множеств, real closed fields или любая другая из кучи аксиоматик?
> классической теории множеств
Какая под этой подразумевается? Сама же ZF? Тогда это самозацикленная фраза.
> возможность рассматривать важный для математики, в целом, класс множеств
Ну, у меня нет ни интереса, ни желания обсуждать такие утверждения. Это вопрос дискуссионный.
> Мы потеряем часть классической математики
Кто "мы"? Пострадают прежде всего те, кто занимается теорией множеств.
>>210859
> Почему именно ZF? А почему не интуиционистской теории типов, а почему не аксиом теорката?
Все ясно, очередной петух не может в математику.
Аксиомы теорката, пиздос.
Поссал в ротешник дауну.
>>210913
>теорката
Это не математика.
Сьеби в /зк и там кукарекай про теоркат и прочие хаскели.
>>210856
>Проблема тут в том, что подавляющее большинство - даунята, неспособные в понимание принципиально
Сударь, у Вас подозрения на двач головного мозга. Пройдите в НМУ (матфак, Стекловку) для лечения. Можешь, впрочем и просто открыть их экзамены/листочки и решить, насколько они даунские.
>Если ты имеешь в виду ошибки невнимательности, то причем здесь ошибки из-за недостатка понимания?
По секрету скажу, что ошибки там далеко не только из-за невнимательности.
>Я же сказал: изучить предмет с полноценным пониманием и без никаких урезаний, что обучаясь в ВУЗе сделать невозможно.
До какой степени тебе надо изучить математику? Матан+линейная алгебра? Два курса НМУ? Мотивы Воеводского?
>Бессмысленное утверждение. А еще математику изучать тяжело. Дальше что?
Тяжело. А так еще тяжелее. Может никаких времени с мотивацией не хватить.
>А зачем ответы на вопросы, ответы на которые получишь гораздо позже в процессе обучения?
Так как иначе сложнее и непонятнее. Вот ты например хочешь с "полноценным пониманием" - его порой нельзя достичь, обучаясь последовательно. А еще не возвращаясь обратно порой. Понимание вообще штука сложная, а ты говоришь, что сам знаешь, когда понимаешь, а когда нет. И вообще последовательно грызть науку можно только до некоторого момента, а потом надо добавлять уже выстрелы наперед, так как иначе совсем пиздец.
>В гугле забанили?
Вроде того. Хочется конкретно про мозги математиков и "качание".
>>210915
>теоркат не математика
Не могу пройти мимо такого осведомлённого человека. Пара вопросов. Почему тензорное умножение точно справа? Почему нельзя отождествлять V и V*, но можно V и V**?
>>210892
Вообще-то функция непрерывная по определению функции Грина. Разрывна только первая производная. Разбивать на участки для применения теоремы о среднем нет смысла. Можно теорему применить сразу и предел интеграла будет ноль. Но почему это аналитически не получается?
>>210943
Ты,выблядок, понимаешь, что теория типов - это модель(!) интуционисткой логики. Теоркат - язык, который никак не противоречит ZFC, еще бы блять он противоречил, ты вообще про категорию Set слышал, мудило?
Теоркат имеет прямое применение(впрочем. откуда он и возник) в гомологической топологии, спектралки считать, пздц.
Про наркомана Гротендика я вообще молчу, он так горел теоркатом, что даже Топос придумал, с помощью которого можно строить логику и на ней теории, включая ZF при желании. Но кому это нужно? Да никому ебать.
Очередной восхищенный теоркатом петух, вот кто ты.
Теоркат, лично мне, пригодился при подсчете спектралки, когда с помощью скрещенного эффекта функтора можно было сказать, что все стрелки в спектралке нулевые.
А взгляд на гомологии и гомотопические группы становится более естественным. А уж про функторы Ext и Tor я молчу, это любому понятно, что тут нужен теоркат.
Теоркат - это просто, сука просто язык.
Вы же блять тут со своим хаскеллом лезете и думаете, что это ВАУ КАК КЛАССНО НИХУЯ НЕ ПОНЯТНО.
мимо-тополог
>>210954
> мимо-тополог
Да перед кем ты выёбываешься? Ты же студентик сраный, куда тебе ТОПОЛОГОМ себя именовать. Степень сначала получи, дурашка, и работать начни. На форчане тоже таких много - первокурсота всякая, подписывающаяся физисистами.
>>210954
Я мимо физик-теоретик из гермашки на пхд.
Дифгем прогуливал, но мне вот интересно, как ты думаешь, что может означать вычисление континуальных интегралов по когомологиям комлексов?
Я считаю это вообще определением физики как таковой.
>>210954
Выдохни, ты порешь несвязную ахинею. Ты спизданул хуйню -- я тебя еблом в дерьмо мокнул, как всегда. Когда ты уже перестанешь на одни и те же грабли наступать?
>>211008
>КОКОКО КУКАРЕКУ Я МАМКИН НИГИЛИСТ И ПРОЕЦИРУЮ 24/7
Ясно)
>>211007
Ты когда-то здесь создавал тред?
У тебя ещё работа не шла.
ITT изувеченные форсом хацкеля малолетние дебилы.
А таки неплохо получилось, смешно.
>>211008
Обосрался да еще и кукарекает. А по делу есть что сказать? Аргументы-аргументики?
>>211008
>мокнул
Это деревенское быдло просто очаровательно :3
>>211043
По какому делу? Ты в математике не разбираешься, с тобой говорить -- только время зря терять.
>>211148
Опять проецируешь))
>>211040
Я создавал тред джва года назад, когда заходил на эту доску в последний раз.
Работа так и не идёт и вообще я на каникулах в России и не факт, что вернусь.
Поостыл интерес. Надоело тратить энергию.
Подвернулась работа риск-аналитиком на банки, да ещё и в моём родном городе.
Да ещё и платят, как в Германии (а у меня тут мухосрань сибирская, но милая).
Планирую остаться в рашке и послать науку к хуям, оставив её в качестве хобби.
Везде был, все видел. Хочу домик в пригороде в Сибири, не сложную работу и рисовать картины :3
А наукой я могу и для души заниматься. Уже 27 лет, что поделать. Приоритеты меняются.
Не хочу всё силу отдавать науке. Детей хочу и пиво у камина.
>>211160
>Подвернулась работа риск-аналитиком на банки
Нассим Талеб поссал тебе в глотку
>>211160
Погоди, так ты не тот, который писал в своем треде (тоже примерно 2 года назад), мол, еще не опустились до нульчановского /g, но уже где-то близко, так что давайте просвещу. Там еще на пикрелейтед анимешный кот был.
Но ОП того треда писал, что он успешно устроился хуярить над КТП и у него дохуя денег и каждые выходные по шлюхам ходит. Это что, ирония была?
То есть ты не видишь ничего нереального в идее хуярить теории самостоятельно дома?
>>211160
Ебал рот макакин с его спам-листом. Сообщение на пике.
>>211186
>>211179
Да, это был я.
Нихуя себе! Меня помнят.
Да, я переписывался с тобой в аське.
Что могу сказать..перегорел я нахуй.
Денег и вправду было много и по шлюхам ходил.
Сейчас уже три недели у себя в Сибири.
И понимаю, что НИКАКОГО желания возвращаться в Гермашку и в науку у меня просто напросто нет.
Мне здесь так охуенно, как в Ницце. Все говорят на моём языке. Солнце светит без остановки.
Люди по улицам ходят толпами!
Вообще, покажи тред где ты кучкуешься.
Как сам? Как работа?
Я лично уже практически обосрался со своим ПХД. Одна статья хилая за два года - не катит.
Сейчас иду на собеседование в компанию по риск аналитике (там директор физик-теоретик с моего вуза, лол).
Возьмут - останусь в России. А наука останется хобби. Всё. Я сгорел и доказывать ничего не хочу ни кому.
Дом себе построить хочу и бабу постоянную наконец-то. А статейки пописывать раз в год на интересующую МЕНЯ тему могу и с корешами по Альма-матер.
>>211190
Ты сделал меня грустить. Наверное, я слишком наивен. И маленький еще. Но у меня все выйдет.
проходил, да не смог не остановиться
>>211194
Ну..напиши пару статеек, поступи в аспирантурку, поживи пару лет в европе. Потом, когда поймёшь, что тебе реально надо и весь этот подростково-студенческий задор пройдёт, рассуждать станешь трезвее. Я просто понял, что в науке я в любом случае останусь. Для меня занятие какой-либо научной деятельностью - это просто свойтво метаболизма. Как посрать. И мне не обязательно класть свою жизнь за это и становится МЕГАЗВЕЗДОЙ.
Я построю себе домик в мирном сибирском городке, обложу дорожки плиточкой, получу непыльную работку при банке и буду растить детей. А статьи я могу писать и так, мне не нужно никакое европейское пхд. Просто буду ходить к друзьям в альма-матер и по выходным вести научные разговоры. Раз в год писать какие-нибудь сумасбродные статьи в соавторстве, понятные только 5 людям в мире.
Но это будет СВОБОДА.
Да. Постарел и обыдлился.
А может взрослее стал. Моя наука всегда со мной в любом случае. А степень получить - дело не долгое. Но обсираться я за неё никогда не буду больше.
>>211190
Вот мой тред: https://2ch.hk/sci/res/207522.html. Я там достаточно отписал.
Мне 28, кстати, можно сказать, ровесники, но я пока не дошёл до черты, когда мог бы сказать "заебало". Но мысли определённые были. So far, держусь, по уши в работе, даже маленькую награду выиграл со своей статьёй одной. Публикаций, которые можно указать в CV, около 6. Ещё одна на повторном ревью (ревьюеры - мои конкуренты блядь) и ещё пишу ревью на одну статью от 4-х китайцев. Ещё две пишутся, одна вот-вот, сижу, хуярю без выходных. Ещё патент отлёживает свои положенные 1.5 года.
С другой стороны, я смотрю на своих приятелей-постдоков и от их убожества тошнит. По 35 лет и никаких перспектив, ни семей, ни кола, ни двора. Одна девчонка недавно получила контракт на два месяца. А ей 34. Скоро она снова переезжает, 3-й раз за год.
У меня хорошо тут женщина своя, русская, смогла переехать ко мне, тоже в науке. Вместе превозмогаем, короче. Но о семье, конечно, и речи пока не идёт.
Короче, пока что меня завлёк профессор остаться интересным проектом, на который я идеально подхожу. Грит, попробуйте, может, через пару лет удача обернётся и станете юниорпрофессором, скажем. А нет, ну что ж ... Придётся писать бевербунги в индустрию. Мне будет 30, думаю, не все шансы будут потеряны.
>>211195
>построю себе домик в мирном сибирском городке
Не думал о том, что рашка в ближайшее время может быть ВСЕ и ты обломаешься со своим домиком?
>>211221
Ну рашка может быть и не ВСЁ но вот нашему милому ватнику-возвращенцу придётся НИЧЕГО ДЛЯ СЕБЯ ВСЁ ДЛЯ РОССЕЮШКИ под присмотром компетентных органов.
>>211224
>свинолюди
У вас вата порвалась.
>>211265
>Ничего, что у меня тут и зарплата и качество жизни выше, чем в гермашке
Ничего что это не надолго?
По социальным вопросам приглашаю всех сюда:
https://2ch.hk/sci/res/207522.html
Не нашёл информачского треда, поэтому спрошу здесь.
Кто-нибудь толком может объяснить, почему задача коммивояжёра NP-трудной?
>211339
>задача коммивояжёра является NP-трудной
Быстрофикс
>>211339
Потому что проверка решения осуществляется за полиномиальное время. Но неизвестен алгоритм вычисляющий решение за полиномиальное время.
>>211339
>>211342
Потому что она не проще NP-полных задач. И да, NP-трудные задачи не относятся к классу NP. Проверка решения не осуществляется за полиномиальное время (если у тебя есть решение задачи, претендующее на минимум, то чтобы удостовериться, что оно действительно минимальное, тебе нужно перебрать все остальные). Но если добавить к ней ограничение, что длина пути-решения должна быть не больше некоторой константы, тогда задача коммивояжера из NP-трудной становится NP-полной (и уже относится к классу NP - нужно просто сравнить длину пути-решения с заданной константой).
Есть ли литература, которая объединяла бы в себе историю науки и изложение её достижений с доказательствами? А ещё чтобы там были приложения в смежных дисциплинах.
Например, начиная от античных математических открытий. Вот, Евдокс открыл то-то и то-то, смотрите, вот выкладка из диалога Платона (математик Евдокс был платоником и, я уверен, засветился в его диалогах), вот, смотрите, неутомимый Аристотель (а лучше Архимед) применил его открытие для объяснения такого-то физическое явления так. И т.д.
Классно же. Ну, можно не такой труд, которые охватывает все эпохи, но хоть что-то.
На ум приходит Гиндикин с рассказами о математиках.
В общем, хотелось бы изучать математику и её приложения, но что именно брать в руки, не знаю.
>>211265
>у меня тут и зарплата и качество жизни выше, чем в гермашке?
Проиграл с этого ПОВЗРОСЛЕВШЕГО.
>>211265
>Ничего, что у меня тут и зарплата и качество жизни выше, чем в гермашке? Свалите короче, подростки хреновы.
Не-подросток нихуя не знает об оценке рисков.
>>211455
По-поводу редкости:
Зарплата в какой-нибудь захудалой компании в Москве, которая занимается чем-то вроде расчета тарифов ЖКХ может легко доходить до 200 тыс. уже через год-полтора.
(работает знакомый со схожим моему физ.образованием). Зарплата Пхд в Европе - 65 тысяч на наши. Знакомые ровесники из Москвы надо мной смеялись.
Но это Москва, фиг с ней.
Ни ОДИН знакомый программист в возрасте 25-30 лет не получает меньше полтинника даже у меня в мухосранске(!).
Подчеркиваю - программист с математическим или около образованием, а не макака-самоучка-дизайнер.
В той же Сибири, варианты для физика, вместо съеба на Ph.D (за 1500 евро) в Германию:
1)Нефтяные компании, меньше 100 там научный сотрудник, моделирующий какую-нибудь гидродинамику и отдачу резервуара не получает (через год). Почти все как один они - математики/физики.
2)Банки, риск-аналитика, программирование в банках. Тот же САП. Там тоже редко встречается что-то меньше 50 (хотя может и не сразу, сраному стажеру конечно не будет такого).
3)Море маленьких и годных IT-компаний. Умели бы искать. 2gis например новосибирская компания.
Итд.
Я перечислил именно варианты, куда может пойти вчершний выпускник физмата из мухосранска без особого опыта помимо аспирантуры зарубежом. Все эти варианты обеспечивают и большую зарплату и лучшие перпективы, чем аспирант-Пётр, вкалывающий за 1500 евро на Ph.D день и ночь, а к 30 оказывающийся в чужой стране с ярлыком overeducated и без работы, когда ровестники становятся начальниками отделов в России с зарплатой в 4 раза больше.
Всё не так однозначно.
Но это именно материальная сторона вопроса (а учёных она редко интересует..на первых порах). Вот такое вот ватное мнение, испытанное на собственной шкуре.
>>211470
Лол, никто не спорит, что зарплата выше и прочее. Речь о том, что завтра накатится очередные санкции и твоего банка не станет, как не стало уже многих.
Ну или царю блажь взбредет еще гаечки подзакрутить и вкалывание за 1500 евро в загнивающей гейропе покажется раем.
>>211478
Раскрою секрет:
Вероятность того, что мой банк закроется или я буду нелиберально ущемлен кровавым путеным итд. существенно меньше вероятности оказаться "не к пизде пришей рукавом" в чужой стране по окончанию 3-летнего ph.d контракта.
Впрочем, никого убеждать не собираюсь.
Просто советую взвешивать решения серьёзней.
Порою тупое подростковое желание "свалить из сраной Рашки" может просто загубить и карьеру и личную жизнь и научные перпективы в том числе. Да только юным сбегаторам от мамки этого не объяснить. Ватником кличуть.
Порою просто следует открыть глаза и трезво оценить свои перпективы. Когда я уезжал из "сраной Рашки" (не скрою, мечтал), я уже работал в местной нефтяной компании.
Какой ебучий черт меня дернул переехать - не знаю. Науки мне захотелось. Сейчас, зная должности и зарплаты моих ровестников, оставшихся в России у меня просто синхротронный бугурт.
Конечно, это касается только материальной строны.
Если действительно ХОТИТЕ НАУКИ, то вероятно лучше ехать на запад. Да вот беда, после окончания пхд под 99% постдоков идут работать в те же банки и нефтяные компании.
Короче, поймите, чего вы на самом деле хотите: НАУКИ или ЗАРПЛАТЫ И УРОВНЯ ЖИЗНИ. Если второго, то на запад ехать вовсе не обязательно, а порою и очень вредно.
Вот такие неочевидные выводы.
PS
Да и наукой на пхд вам вряд ли дадут свободно заниматься.
Будете численной макакой или чем-то в этом духе.
>>211486
>Вероятность того, что мой банк закроется или я буду нелиберально ущемлен кровавым путеным итд. существенно меньше вероятности оказаться "не к пизде пришей рукавом" в чужой стране по окончанию 3-летнего ph.d контракта.
Прописываю живительную дозу Черного Лебедя.
>>211343
Меня интересует само доказательство, о том, что ты мне сообщил здесь, я знал.
Ув. господа, помогите новичку решить одну задачу по математике:
Пусть а1,а2,а3,an - какие-либо действительные числа и f(t)=cos(t+a1) + 1\2*cos(t+a2) .... + 1/2^(n-1)*cos(t+an).
Причем f(t1)=f(t2)=0. Доказать что t2-t1=m*Pi, где m некоторое целое число.
Задача находится в книге о комплесных числах ( я нюб, школоло, только начал учить), так что если можно решение прибегая к ним.
>>211470
Всё так.
Другой Гермашка-кун
Но наука чертовски завлекает. Сегодня мне пришёл ответ, что статью-таки примут с парой мелких поправок
>>211530
t1, t2 могут быть комплексными или только действительными?
>>211540
Поясни за вот какую сторону вопроса: я химик, планирую после бакалавриата поступить в немецкий университет, но наслышан о проблемах с дальнейшей научной карьерой, так что после магистра хотел бы работать в Bayer AG, BASF или где ещё, да и прикладной наукой заниматься сподручнее, мне кажется. Проблем с трудоустройством и получением вида на жительство после окончания университета не возникает? Чем нужно озаботиться?
>>211542
В задаче ничего об этом не оговорено, но мне кажется что толк действительными. У меня есть некие мысли про то как ее решать, но я просто не знаю, могу ли я нагло взять и заменить такое выражение: e^(ia)+(1\2)*e^(ia2)... + ((1\2)^(n-1))*e(i*an) на какое то левое типа p*e^(какая нибудь)
тоесть смысл в том, могу ли я наплевать просто на аргументы комплексных чисел и их модули и представить что их сумма в итоге станет каким-нибудь комплексным числом, а каким нам уже не важно. С другой стороны получается, то, что нам вообще неважно какие были модули у комплексных чисел и все эти прогрессии с 1\2 просто для забития баков?
>>211530
Она без комплексных чисел решается.
Запишем f(t)=0. Преобразуем каждый член функции как косинус суммы и перенесём синусы в другую сторону:
cos(t)cos(a1) + 1/2*cos(t)cos(a2) + ... + 1/2^(n-1)*cos(t)cos(an) = sin(t)sin(a1) + 1/2*sin(t)sin(a2) + ... + 1/2^(n+1)*sin(t)sin(an)
Вынесем cos(t) и sin(t) слева и справа. Теперь поделим на cos(t)*(sin(a1) + 1/2*sin(a2) + ... + 1/2^(n-1)*sin(an)):
(cos(a1) + 1/2*cos(a2) + ... + 1/2^(n-1)*cos(an)) / (sin(a1) + 1/2*sin(a2) + ... + 1/2^(n-1)*sin(an)) = tg(t)
Отсюда t = arctg(большая фигня слева). Периодичность функции T = pi, значит t1-t2=m*pi. ЧТД.
Я не рассматривал случаи, когда какой-то из множителей равен нулю, тогда получим синус или косинус равен нулю, а нули синуса и косинуса идут через pi, что то же самое.






























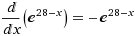



















































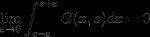














Продолжаем треды, посвящённые лучшей из наук.
И начнём с глупого вопроса, который остался с прошлого треда. Почему аксиомы булеана, выделения и замены неконструктивны?
Previous: http://2ch.hk/sci/res/198318.html